37. Скалярное произведение векторов. Свойства. Доказательство одного свойства. Скалярное произведение

Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними

Свойства скалярного произведения

1. Необходимое и достаточное условие перпендикулярности векторов – скалярное произведение векторов равно 0:

2. 

так как

3. 

4. 

так как

5. 

так как

Следствие. Свойства 3 и 4 могут быть записаны в виде формул

Будем говорить, что последние формулы отражают свойство линейности скалярного произведения соответственно относительного первого и второго сомножителей.

6. Скалярный квадрат вектора равен квадрату длины вектора

Действительно,

7. , причем если

8. Если то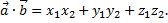

Доказательство.

так как

9. 

10. .

38. Векторное произведение векторов. Свойства. Доказательство одного свойства. Определение векторного произведения

Векторным произведением векторов называется вектор , удовлетворяющий условиям

1. где угол между векторами

2. 

3. образуют правую тройку.

При этом пишут или Если векторы неколлинеарны, то вектор векторного произведения перпендикулярен плоскости, определяемой векторами приведенными к общему началу (рис. 1).

Рис. 2

Свойства векторного произведения

1. Необходимое и достаточное условие коллинеарности векторов - их векторное произведение равно : .

Доказательство.

Необходимость. Пусть векторы коллинеарны. Это возможно в 2 случаях:

1) один из векторов нулевой; тогда

2) угол между векторами (векторы сонаправлены) или (векторы противоположно направлены), для обоих углов поэтому

Достаточность. Пусть тогда Поэтому либо один из векторов нулевой, либо Так как угол между векторами удовлетворяет неравенству то или Следовательно, векторы коллинеарны.

2. Длина векторного произведения неколлинеарных векторов равна площади параллелограмма, построенного на векторах-сомножителях, приведенных к общму началу

Действительно, обе величины равны

3. 

Доказательство. Если векторы коллинеарны, то векторное равенство верно, так как оба вектора нулевые. Будем считать, что векторы неколлинеарны. Обозначим и угол между векторами Ясно, что то есть Векторы и коллинеарны, так как они перпендикулярны плоскости, определяемой векторами По определению векторного произведения тройки и правые, а это влечет за собой противоположную направленность векторов и (рис.3). Поэтому векторы и противоположны, то есть

Рис. 3

4. Векторное произведение линейно относительно обоих сомножителей

Доказательство позже.

Декартова прямоугольная система координат называется правой, если базисные векторы системы координат образуют правую тройку. Если особо не оговорено, всегда предполагается, что система координат является правой.

5. Если ортонормированный базис декартовой прямоугольной системы координат, то

Доказательство. Докажем первое равенство, остальные доказываются аналогично.

1. Длины векторов и равны единице, следовательно,

2. Векторы и коллинеарны, так как они перпендикулярны плоскости векторов .

3. Векторы и сонаправлены, так как векторы образуют правую тройку.

Следовательно, векторы и равны.

6. Если известны координаты векторов то

Доказательство. Если ортонормированный базис декартовой прямоугольной системы координат, то

Используя свойства 1,3,5, получаем

Замечание. Для запоминания последней формулы используют определитель

Действительно, раскладывая определитель по элементам первой строки, получаем