Каноническое уравнение, параметрические уравнения прямой

Пусть на плоскости задана прямая и выбрана декартова прямоугольная система координат. Пусть Ненулевой вектор , лежащий на прямой называется направляющим вектором прямой.

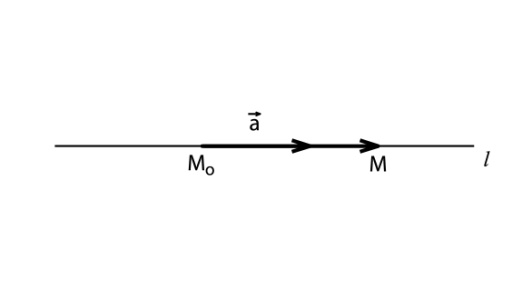
Выберем произвольную точку Если то и существует такое число , что здесь параметр, Так как то получаем

(5)

Уравнения (5) называются параметрическими уравнениями прямой.

Если то из уравнений (5)

можно исключить параметр

Уравнение (6) называется каноническим уравнением.

Если одно из чисел равно 0, также используют каноническое уравнение (6), полагая, что, если знаменатель дроби равен 0, это означает, что числитель равен 0. Например, если то из уравнений (5)

Так как то второе равенство означает, что любое. Поэтому в этом случае уравнение прямой параллельной оси Каноническое уравнение

Уравнение прямой, проходящей через две точки

Выведем уравнение прямой, проходящей через 2 точки и Вектор является направляющим вектором прямой, в качестве начальной точки можно взять любую из точек . Подставляя в каноническое уравнение его координаты, получаем

Последнее уравнение и есть уравнение прямой, проходящей через точки

Уравнение прямой с угловым коэффициентом

Рассмотрим прямую, не параллельную оси В этом случае из параметрических уравнений

может быть исключен параметр

Уравнение (7) является уравнением прямой с угловым коэффициентом. Обычно коэффициент обозначают

Можно проверить, что равен тангенсу угла наклона прямой к оси Этим объясняется название коэффициента.

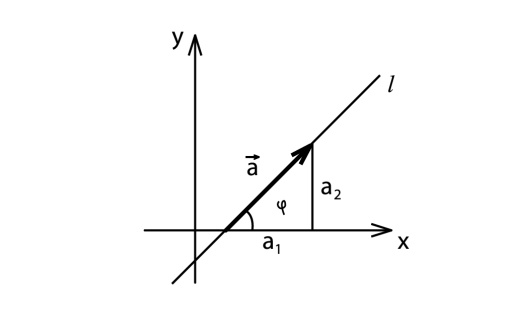
Если раскрыть скобки в уравнении (7) и сгруппировать числа, то получим еще одну форму уравнения прямой с угловым коэффициентом

Взаимное расположение двух прямых на плоскости

1. Если две прямые заданы общими уравнениями

то взаимное расположение прямых определяется с помощью векторов нормалей к прямым и .

Условие параллельности и или

Прямые и совпадают, если

Условие перпендикулярности и или

Угол между прямыми и : определяется с помощью угла между нормалями

2. Если две прямые заданы каноническими уравнениями

здесь - направляющие векторы прямых и Тогда с помощью направляющих векторов могут быть выписаны условия параллельности и перпендикулярности прямых.

Условие параллельности и или

Условие перпендикулярности и или

Угол между прямыми и : определяется с помощью угла между направляющими векторами

3. Пусть две прямые заданы уравнениями с угловыми коэффициентами

здесь - начальные точки прямых, - угловые коэффициенты прямых.

Условие параллельности и так как

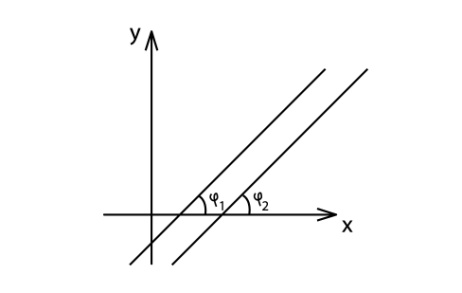
Условие перпендикулярности и

Запишем уравнения прямых в виде:

Тогда векторы нормалей и Тогда условие перпендикулярности прямых или

Угол между прямыми и : определяется с помощью угла

Действительно,