28. Розкрийте зміст поняття невизначеність. Наведіть головні відмінності концепції невизначеності від концепції похибок.
Невизначеність вимірювання (англ. measurement uncertainty) — параметр, що пов'язаний з результатом вимірювання та характеризує розсіяння значень, які обґрунтовано могли б бути приписані вимірюваній величині
Оскільки на практиці вимірюваній величині приписуються значення, отримані в результаті вимірювання (результати вимірювання), то вказаний параметр характеризує розсіяння результатів вимірювання.
Головна відмінність концепції невизначеностей від концепції похибки результату вимірювання – відхід від поняття "істинне значення вимірюваної величини" як такого, що не піддається пізнанню. За цих умов втрачає зміст поняття "похибки вимірювання" як відхилення результату від істинного значення вимірюваної величини. Натомість, у метрологічній практиці з’явилися нові терміни, зокрема невизначеність вимірювання, стандартна, сумарна і розширена невизначеності та інші.
29. Наведіть класифікацію невизначеності за формою подання
Подаючи результат вимірювання, використовують наступні форми невизначеності [13]: стандартна невизначеність, комбінована стандартна невизначеність, розширена невизначеність.
Стандартна невизначеність - невизначеність результату вимірювання, виражена у вигляді СКВ. Її позначення в керівному документі ІSO - U
Комбінована стандартна невизначеність - стандартна невизначеність результату вимірювання, яку використовують, коли результат вимірювання отримано під час вимірювання інших величин. Комбінована стандартна невизначеність дорівнює додатному кореню із суми складових (дисперсій чи коваріацій вимірюваних величин), зважених відповідно до впливу вимірюваних величин на результат вимірювання. Її позначення в керівному документі - Uс
Розширена невизначеність – невизначеність у вигляді інтервалу біля результату вимірювання, в який потрапляє більша частина розподілу можливих значень вимірюваної величини. Її позначення в керівному документі ISO - U
Розширену невизначеність обчислюють за формулами:
через стандартну невизначеність U = KU
через комбіновану стандартну невизначеність U = Kuc.
В цих формулах К - фактор (коефіцієнт) покриття – це числовий коефіцієнт, що використовують як множник, щоб отримати розширену невизначеність.
30. Наведіть класифікацію невизначеності за методами оцінювання.
За методами оцінювання невизначеності поділяють на дві групи
Оцінювання невизначеності за типом А
1. Якщо кількість дослідів n < 10, uА не оцінюють. Для 10 ≤ n < 20 – якщо закон розподілу
ймовірностей невідомий, для оцінювання uА приймають рівномірний закон. Якщо n ≥ 20 – закон розподілу ймовірностей визначають апроксимацією експериментальних даних.
2. Для прямого вимірювання результат визначають як середнє арифметичне отриманих значень,
тоді невизначеність за типом А обчислюють за формулою:
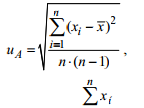
3. Для опосередкованого вимірювання результат визначають за оцінками декількох величин, тоді
невизначеність за типом А обчислюють для кожної вихідної величини:
- якщо значення величини розподілені за рівномірним законом, за формулою:
де b – півширина інтервалу (для несиметричного закону розподілу b =( (b+) +( - b)/2);
- якщо значення величини розподілені за нормальним законом, невизначеність обчислюють як
середньоквадратичне відхилення, за формулою:
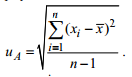
У випадку коли дисперсія результатів врахована у невизначеності, то додатково похибку ЗВТ
враховувати непотрібно – вона відображена у дисперсії.
Оцінювання невизначеності за типом В
1. Ґрунтуючись на рівнянні залежності вимірюваної величини від вихідних величин складають
переліки: вимірюваних вихідних величин; не вимірюваних впливових вихідних величин; введених поправок
на відомі систематичні похибки; коефіцієнтів і констант; додаткових похибок тощо.
2. Невизначеності усіх вхідних величин оцінюють інтервалами і перетворюють їх у
середньоквадратичне відхилення, при цьому закон розподілу їхніх ймовірностей, якщо він невідомий,
приймають рівномірним. Формула перерахування інтервальної оцінки у середньоквадратичне відхилення:
де σ – середньоквадратичне відхилення; b – на півширина інтервалу; t – значення функції Лапласа для
нормального закону розподілу ймовірностей (або аналог значення функції Лапласа для іншого закону).