3.3. Приложение определенного интеграла.
Справочный материал:
площадь плоской фигуры, ограниченной линиями:
объём тела с площадью поперечного сечения:
.
Примеры.
Построить схематический чертеж и найти площадь фигуры, ограниченной линиями :
Найдем точки пересечения линий.
Раздел 4. Теория вероятностей
и математическая статистика
Случайные величины и их характеристики
Случайной
величиной
называется числовая функция, определенная
на пространстве элементарных исходов
,
которая каждому элементарному исходу
ставит в соответствие число
.
Условимся
в дальнейшем, как правило, случайные
величины обозначать греческими буквами:
,
,
…, а принимаемые ими значения – строчными
латинскими (с индексами или без):
,
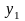и т.д.
Случайные величины делятся на дискретные и непрерывные.
Случайная
величина называется дискретной,
если значения, которые может принимать
данная случайная величина, образуют
дискретное (конечное или бесконечное)
множество чисел
,
,
…,
,
…
Под
непрерывной
случайной величиной будем понимать
величину, значения которой, заполняют
конечный или бесконечный промежуток
числовой оси
.
Например, число студентов на лекции – дискретная случайная величина, продолжительность лекции – непрерывная.
1.6. Дискретная случайная величина и ее числовые характеристики
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Закон распределения дискретной случайной величины обычно задается рядом распределения, который представляется в виде таблицы:
|
|
|
… |
|
|
|
|
… |
|
где в
первой строке перечислены все возможные
значения случайной величины, а во второй
– соответствующие им вероятности
,
удовлетворяющие соотношению
.
Закон
распределения может быть задан графически
в виде многоугольника
распределения вероятностей,
т.е. в виде ломаной, соединяющей точки
с координатами
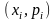для
.
Математическим ожиданием или средним значением дискретнойслучайной величины называется сумма произведений всех ее возможных значений на соответствующие им вероятности:
. (1)
Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, т.е.
. (2)
Для вычисления дисперсии на практике бывает удобнее использовать другую формулу, которую можно получить из формулы (8) с помощью простых преобразований:
. (3)
Средним квадратическим отклонением или стандартным отклонением случайной величины называется корень квадратный из ее дисперсии:
.
Раздел 5. Основы теории комплексных чисел
Сначала
вспомним «обычные» школьные числа. В
математике они называются множеством
действительных чисел и
обозначаются буквой 
(в
литературе, рукописях заглавную букву
«эр» пишут жирной либо утолщённой). Все
действительные числа сидят на знакомой
числовой прямой:
Компания действительных чисел очень пёстрая – здесь и целые числа, и дроби, и иррациональные числа. При этом каждой точке числовой обязательно соответствует некоторое действительное число.
Комплексным
числом 
называется
число вида 
,
где 
и 
–
действительные числа, 
–
так называемая мнимая
единица.
Число
называется действительной
частью (
)комплексного
числа
,
число
называется мнимой
частью (
) комплексного
числа
.
–
это ЕДИНОЕ
ЧИСЛО, а не сложение. Действительную и
мнимую части комплексного числа, в
принципе, можно переставить местами: 
или
переставить мнимую единицу: 
–
от этого комплексное число не изменится. Но
стандартно комплексное число принято
записывать именно в таком порядке:
Чтобы всё было понятнее, сразу приведу геометрическую интерпретацию. Комплексные числа изображаются на комплексной плоскости:
Как
упоминалось выше, буквой
принято
обозначать множество действительных
чисел. Множество комплексных
чисел принято
обозначать «жирной» или утолщенной
буквой 
.
Поэтому на чертеже следует поставить
букву
,
обозначая тот факт, что у нас комплексная
плоскость.
Комплексная плоскость состоит из двух осей: – действительная ось – мнимая ось
Построим
на комплексной плоскости следующие
комплексные числа:
, 
, 
, 
, 
, 
, 
, 
Рассмотрим следующие комплексные числа: , , . Вы скажете, да это же обыкновенные действительные числа! И будете почти правы. Действительные числа – это частный случай комплексных чисел. Действительная ось обозначает в точности множество действительных чисел , то есть на оси сидят все наши «обычные» числа. Более строго утверждение можно сформулировать так: Множество действительных чисел является подмножеством множества комплексных чисел .
Числа , , – это комплексные числа с нулевой мнимой частью.
Числа , , – это, наоборот, чисто мнимые числа, т.е. числа с нулевой действительной частью. Они располагаются строго на мнимой оси .
В числах , , , и действительная и мнимая части не равны нулю. Такие числа тоже обозначаются точками на комплексной плоскости, при этом, к ним принято проводить радиус-векторы из начала координат (обозначены красным цветом на чертеже). Радиус-векторы к числам, которые располагаются на осях, обычно не чертят, потому что они сливаются с осями.