
- •Раздел 1. Теория пределов функций и непрерывность и разрывы функций.
- •1.2. Точки непрерывности и точки разрыва функции.
- •Раздел 2. Дифференциальное исчисление
- •Правила дифференцирования:
- •Раздел 3. Интегральное исчисление
- •3.1. Неопределенный интеграл.
- •Основные свойства интегрирования:
- •3.2. Определенный интеграл.
- •3.3. Приложение определенного интеграла.
- •Раздел 4. Теория вероятностей
- •Случайные величины и их характеристики
- •1.6. Дискретная случайная величина и ее числовые характеристики
- •Раздел 5. Основы теории комплексных чисел
- •Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел
- •Тригонометрическая форма комплексного числа
- •Раздел 6. Основы дискретной математики
- •6.1.Элементы теории множеств
- •Отношения между множествами
- •Раздел 7. Основы линейной алгебры
- •7.1. Операции с матрицами
- •7.2. Определители.
- •7.3. Решение систем линейных алгебраических уравнений.
- •Раздел 1. Теория пределов функций
- •Раздел 2. Дифференциальное исчисление
- •Раздел 3. Интегральное исчисление
- •Раздел 4. Теория вероятностей и математическая статистика
- •Раздел 5. Основы теории комплексных чисел
- •Раздел 6. Основы дискретной математики
- •Раздел 7. Основы линейной алгебры
- •Формирование исходных данных к заданиям
- •Рекомендации по оформлению практических (контрольных) работ
- •Список исплользуемой литературы
- •Перечень вопросов к экзамену по дисциплине математика
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ДИСЦИПЛИНЕ
МАТЕМАТИКА
для студентов заочной формы обучения
СОДЕРЖАНИЕ:
стр.
РАЗДЕЛ 1. ТЕОРИЯ ПРЕДЕЛОВ ФУНКЦИЙ 3
Раздел 2. Дифференциальное исчисление 8
РАЗДЕЛ 3. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ 16
раздел 4. Теория вероятностей и
математическая статистика 23
раздел 5. Основы теории комплексных чисел 25
раздел 6. Основы дискретной математики 31
раздел 7. Основы линейной алгебры 34
ИНДИВИДУАЛЬНЫЕ ТИПОВЫЕ ЗАДАНИЯ 38
СПИСОК ЛИТЕРАТУРЫ 40
ПЕРЕЧЕНЬ ВОПРОСОВ К ЗАЧЕТУ (ЭКЗАМЕНУ) 41
Раздел 1. Теория пределов функций и непрерывность и разрывы функций.
Справочный материал.

1.2. Виды неопределенности и способы их раскрытия
неопределенность
 раскрывается с помощью деления числителя
и знаменателя на старший член выражения,
приводя таким образом к бесконечно
малым и постоянным величинам, и
использования пределов:
раскрывается с помощью деления числителя
и знаменателя на старший член выражения,
приводя таким образом к бесконечно
малым и постоянным величинам, и
использования пределов:

неопределенность
 при х
→ а
в алгебраических выражениях раскрывается
разложением на множители числителя и
знаменателя и сокращения множителей
(х
- а);
при х
→ а
в алгебраических выражениях раскрывается
разложением на множители числителя и
знаменателя и сокращения множителей
(х
- а);неопределенность в тригонометрических выражениях раскрывается с помощью первого замечательного предела

 ;
;неопределенность
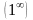 раскрывается с помощью второго
замечательного предела
раскрывается с помощью второго
замечательного предела
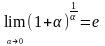 .
.
Примеры решения задач.
Найти пределы функций:
а)
 [делим
на
[делим
на
 числитель и знаменатель]=
числитель и знаменатель]=

б) [разложим
числитель и знаменатель на множители]
=
[разложим
числитель и знаменатель на множители]
=
 ;
;
в)
 [числитель
и знаменатель умножим на сопряженные
множители
[числитель
и знаменатель умножим на сопряженные
множители
 ]
]

 ;
;
1.2. Точки непрерывности и точки разрыва функции.
Справочный материал.
Необходимые понятия:
-
левосторонний предел

-
правосторонний предел
-
функция
 непрерывна в точке х
= а,
если она в ней определена и
непрерывна в точке х
= а,
если она в ней определена и

- функция разрывная в точке х = а, если хоть одно из условий не выполняется;
-
функция
имеет разрыв первого рода, если существуют
оба односторонних предела, но
 (такой вид разрыва называется скачком),
либо
(такой вид разрыва называется скачком),
либо
 или
не определена в х
= а
(такой вид разрыва называется устранимым);
или
не определена в х
= а
(такой вид разрыва называется устранимым);
- функция имеет разрыв второго рода, если хотя бы один из односторонних пределов не существует или равен ∞.
Примеры решения задач.
Найти возможные точки разрыва функций, определить их характер и изобразить на схематическом чертеже поведение функций в окрестности точек разрыва:
а)

В интервалах (− ∞; 0), (0; 1) и (1; +∞) как элементарная функция в своей области определения.
Исследуем
возможные точки разрыва
 :
:


в точке х1 = 0 имеет разрыв I рода (скачок);


в точке х2=1 непрерывна.

б)

не определена при х = 3, то есть имеет в этой точке разрыв.

в точке х = 3 имеет разрыв II рода.

в)
 не существует при х
= 1 и при
не существует при х
= 1 и при

 - точки разрыва
функции, исследуем их.
- точки разрыва
функции, исследуем их.

в точке х1 = 1 разрыв I рода.

в точке х2
= 2 разрыв
II
рода.
точке х2
= 2 разрыв
II
рода.
Раздел 2. Дифференциальное исчисление
Вычисления производных.
Справочный материал.
Таблица производных элементарных функций:

Правила дифференцирования:

Примеры нахождения производных.
Найти производные у′(х) функций:
Задание
1. Найти
производную функции ![]()
Так как производная суммы равна сумме производных, то
![]()
Воспользуемся формулами для производных показательной и обратной тригонометрической функций:
![]()
Ответ.
Задание
2. ![]()

Задание
3. ![]()
Применим последовательно правило дифференцирования алгебраической суммы функций и вынесение коэффициента за знак производной:

Задание
4. ![]()
Применим последовательно правило дифференцирования алгебраической суммы функций и вынесение коэффициента за знак производной:

Задание
5. ![]() .
.
Применим последовательно правило дифференцирования алгебраической суммы функций и вынесение коэффициента за знак производной:
 .
.
Задание
6. ![]() .
.
Применим правило дифференцирования произведения функций:

Задание
7. ![]()
Используем правило производной произведения двух функций:

Задание
8. 
Используем правило производной частного двух функций:
 .
.
Наибольшее и наименьшее значение функции на отрезке.
Справочный материал:
- если
функция
непрерывна на отрезке [a,
b],
то она достигает на нем своего наибольшего
 и наименьшего значения
и наименьшего значения
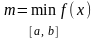 ;
;
- для
нахождения M
и m
достаточно найти критические точки
х1,
х2,
… внутри отрезка [a;b]
и выбрать M
и m
сравнением значений
 ,
,
 ,…
и
,…
и
 ,
,
 ;
;
-
критические точки находятся из уравнения
 или из условий не существования
или из условий не существования
 и непрерывности
в этих точках.
и непрерывности
в этих точках.
Пример.
Найти наибольшее и наименьшее значения
функции
 на
на

 не существует при х1
= 0 – это
критическая точка так как
при х
= 0 непрерывна.
не существует при х1
= 0 – это
критическая точка так как
при х
= 0 непрерывна.
 ,
,
 .
Найдем значения:
.
Найдем значения:

 .
.
Исследование функции на экстремум.
Справочный материал:
- из необходимых условий экстремума и не существует, но непрерывна, находятся критические точки х1, х2, …;
- с помощью знака производной устанавливается наличие и вид экстремума:

 в
в
 в
в
 ,
в
,
в
 нет
экстремума.
нет
экстремума.
Примеры.
ПРИМЕР
1: Исследовать
функцию
 на экстремумы.
на экстремумы.
1.
Область определения D
 .
.
2. Найдем критические точки первого рода:

 критические
точки.
критические
точки.
З нак
нак

 точка А(1; 1) – точка
минимума данной функции.
точка А(1; 1) – точка
минимума данной функции.
Пример 2.
Исследовать
функцию ![]() .
.
Решение.
1. Функция определена и непрерывна на всей числовой оси.
2. Для того чтобы выяснить, является ли функция четной/нечетной, необходимо проверить, выполняются ли равенства
![]() или
или
![]()

Функция не является ни четной, ни нечетной.
3. Найдем
точки пересечения графика функции с
осью ![]() при
при ![]() :
:
![]()
Разложим многочлен на множители, получим
![]()
График функции пересекает ось в точках (2, 0) и (3, 0).
Найдем
точки пересечения графика функции с
осью ![]() . При
. При ![]()
![]() .
.
График функции пересекает ось в точке (0, –12).
4. Производная
функции: ![]() .
.
Решая
уравнения ![]() ,
получим критические точки
,
получим критические точки
![]()
Расположим критические точки на оси абсцисс в порядке возрастания и исследуем знак производной в окрестности каждой критической точки (рис. 1).
|
|
|
|
у’ + 2 - 8/3 + X
Рис. 1

На
интервалах ![]() функция
возрастает, так как
функция
возрастает, так как ![]() На
интервале
На
интервале ![]() функция
убывает, так как
функция
убывает, так как ![]() .
.
5. При
переходе через критическую
точку ![]() производная
меняет знак с минуса на плюс. Следовательно,
в этой точке функция имеет минимум. В
точке
производная
меняет знак с минуса на плюс. Следовательно,
в этой точке функция имеет минимум. В
точке ![]() функция
имеет максимум. Значения функции в
точках экстремума:
функция
имеет максимум. Значения функции в
точках экстремума:
![]() .
.
6. Вторая
производная функции: ![]() .
Решая уравнение
.
Решая уравнение ![]() ,
находим критическую точку второго рода:
,
находим критическую точку второго рода:
![]() .
.
Расположим полученную критическую точку на числовой оси и исследуем знак производной в окрестности этой точки (рис. 2).
|
|
|
|
y” - 7/3 + X
Рис. 2

На
интервале ![]() график
функции выпуклый, так как
график
функции выпуклый, так как ![]() .
На интервале
.
На интервале ![]() график
функции вогнутый, так как
график
функции вогнутый, так как ![]() .
.
7. При переходе через критическую точку второго рода вторая производная функции меняет знак. Следовательно, на основании достаточного условия существования точки перегиба точка является точкой перегиба графика функции.
![]() .
.
8. Найдем асимптоты графика функции.
![]() .
.
Горизонтальных асимптот нет.
Так как функция определена и непрерывна на всей числовой оси, вертикальных асимптот нет:
![]() .
.
Наклонных асимптот функция не имеет.
9. Построим график функции (рис. 3).

Рис. 3
Пример 3. Исследовать функцию и построить ее график
![]() .
.
Решение.
D(f):

 тогда
тогда

2. Функция не является ни четной ни нечетной.
3. Функция
пересекает оси координат в точке ![]() .
.
4. Первая производная функции:
![]() .
.
Решая уравнение ![]() находим
критические точки
находим
критические точки
![]() ,
x3=
-1/
,
x3=
-1/
Расположим их на числовой оси и исследуем знак производной в окрестности каждой из этих точек (рис. 4).
|
|
|
|
y’ + - 2 - -1 - 0 + X
Рис. 4
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
С
учетом того что в точке ![]() функция
не определена, получим: на интервалах
функция
не определена, получим: на интервалах ![]() функция
возрастает, на интервалах
функция
возрастает, на интервалах ![]() убывает.
убывает.
5.
При переходе через критическую
точку ![]() производная
меняет знак с плюса на минус. Следовательно,
в этой точке функция имеет максимум.
При переходе через критическую
точку
производная
меняет знак с минуса на плюс. Следовательно,
в этой точке минимум.
производная
меняет знак с плюса на минус. Следовательно,
в этой точке функция имеет максимум.
При переходе через критическую
точку
производная
меняет знак с минуса на плюс. Следовательно,
в этой точке минимум.
Найдем значения функции в точках экстремума:
![]() .
.
6. Критические точки второго рода: находим вторую производную функции:
![]() .
.
Вторая производная не обращается в нуль, а при функция не определена. Следовательно, критическая точка второго рода.
Исследуем знак второй производной:
|
|
|
|
y” - -1 + X
|
На
интервале ![]() график
функции выпуклый, на интервале
график
функции выпуклый, на интервале ![]() вогнутый.
вогнутый.
7. Так как функция критических точек второго рода не имеет, точки перегиба графика функции отсутствуют.
8. Найдем асимптоты графика функции.
а)
горизонтальных асимптот нет:
![]() .
.
б) вертикальная асимптота – точка разрыва области определения х=-1?
считаем односторонние пределы
![]()
![]() .
.
Следовательно, прямая - вертикальная асимптота.
в)
наклонные асимптоты

![]() ;
;
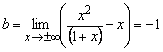 .
.
Следовательно,
прямая ![]() является
наклонной асимптотой графика функции.
является
наклонной асимптотой графика функции.
8. Построим график функции (рис. 3.16).
|
|
|
|



