10.Дифференциалдаушы буын(жиілік сипаттамасы)

Жиіліктіксипаттамалар Жиіліктік беріліс функциясының графигі жорамал осьтің оң бағытына сәйкес келеді

.Буынның логарифмдік амплитудалық сипаттамасының теңдеуі Логарифмдік амплитудалық сипаттама жиілікте ординатасы бар көлбеудегі + 20дБ/дек түзу түрінде болады.Логарифмдік фазалық сипаттама жиілік осіне параллель, оның жоғарғы жағынан + 90° деңгейде өтеді. Демек, дифференциалдаушы буын оң фазалық ығысу тудырады. Нақты дифференциалдаушы буынды идеал дифференциалдаушы және бірінші ретті апериодтық буындарды бір-бірімен тізбектей қосу арқылы алуға болады. Оның дифференциал теңдеуі ал беріліс функциясы Мұндай беріліс функциясы бар буынды инерциясыз және апериодтық буындарды параллель қосу арқылы көрсетуге болады. Дифференциалдаушы буындардың ерекшеліктері:

Буын кірісіне сатылы әсер берген кезде, оның шығысында үлкен қысқамерзімдік импульс туып, өтпелі процесс аяқталғаннан кейін шығыстық айнымалы нөлге тең болады. Егер кірістік сигнал уақыт бойынша өзгермесешығыстық сигнал нөлге тең, ал кірістік сигнал заңдылығымен сызықты өсер болса, онда шығыстық сигнал тұрақты: ;

1. Беріліс функциясына әруақытта көбейткіші кіретіндіктен 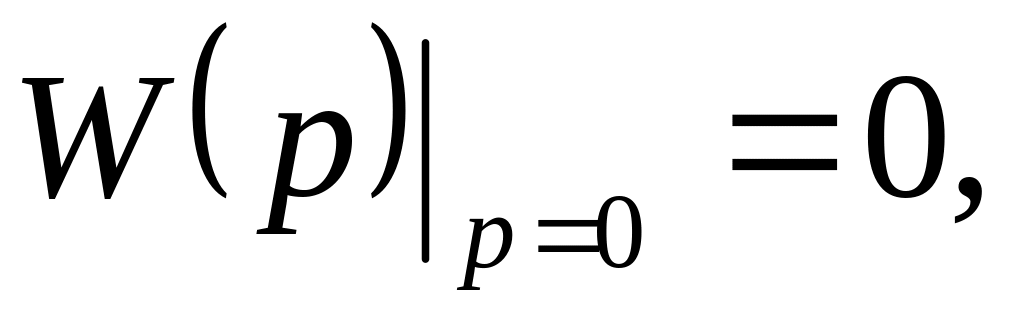және дифференциалдаушы буын статикада кірістік сигналды жібермейді ;

3. Дифференциалдаушы буын жоғарыжиілікті сигналдарды жақсы өткізіп, төменгіжиіліктілерді нашар өткізеді, яғни ол жоғарыжиілікті фильтр ретінде қолданылады.

9.Интегралдаушы буын(жиілік сипаттамасы)

Буынның берiлiс функциясынан мыналарды аламыз: ). Жиiлiк 0-ден -ке дейiн өзгергенде модулi нөлге ұмтылады, яғни буын жоғары жиiлiктi өткiзбейдi

Қозғалтқышқа қатысты айтсак, онда жиiлiк жоғары болған сайын қозғалтқыштың орнынан қозғалмайтындығының ықтималдығы соғұрлым үлкен. Жиiлiктiң барлық мәнi үшiн векторының аргументi -ге тең, яғни шығыстық жиiлiк тербелiсi фаза бойынша кiрiстен бұрышқа қалып отырады. Логарифмдiкамплитудалыксипаттама(6.12.г-сурет). (6.65).жиiлiк осiн нүктесiнде қиып өтетiн тура түзу түрiнде болады. (6.65)-ден бұл сипаттаманың көлбеулiгi -20 дБ/дек болатындығы туындайды. Логарифмдiк фазалық сипаттама жиiлiкке тәуелсiз болып, абсцисса осiне параллель қашықтықта өтедi.

Нақты интегралдаушы буынның сипаттамаларын қарастырайық. Нақты интегралдаушы буынның дифференциалдық теңдеуі ,ал беріліс функциясы Яғни беріліс функциясынан , нақты интегралдауыш буынды беріліс функциясы идеал интегралдауыш буын мен беріліс коэффициенті , уақыт тұрақтысы статикалық апериодты буынды тізбектей қосу арқылы алуға болатынын көреміз. Сондықтан, буынның барлық сипаттамаларын осы екі қарапайым буындардың сипаттамаларынан комплексті шамаларды көбейту ережелеріне сәйкес алуға болады (6.13-сурет).

Интегралдаушы буынның ерекшеліктері:Буынның кірісіне бірлік секірістік сигнал берілген кезде шығыстық шама шексіз өсе бастайды да, өтпелі процесс аяқталғаннан кейін сызықты заң бойынша өзгереді: .Кірістік сигналды беруді тоқтатқаннан кейін де шығыстық айнымалы өзінің жеткен мәнінде қалады, осы себептен интегралдаушы буынды есте сақтаушы элемент ретінде пайдалануға болады (жадты элемент);Беріліс функциясына міндетті түрде көбейткіші кіреді, сондықта ал ;ИБ ТЖФ.