§ 8. Понятие о рядах распределения абсолютных и относительных величин

Ряды распределения — это ряды абсолютных и относительных чисел, которые характеризуют распределение единиц совокупно­сти по качественному (атрибутивному) или количественному при­знаку. Примером распределения совокупности по качественному признаку может быть распределение сотрудников милиции (офи­церов) по специальному званию: полковников — 1, подполков­ников — 3, майоров — 8 ... всего — 50 человек. Эта же совокуп­ность может быть распределена по количественному признаку, скажем, по возрасту: моложе 20лет — 2, 20—24 года— 18, 25— 29 лет — 10 и т. д. В обоих примерах ряды распределения выражены в абсолютных числах. Последние в подобных случаях называются частотами ряда распределения. Они указывают, насколько часто повторяется та или иная варианта (признак). Варианта «майор» имеет частоту 8, а варианта «20—24 года» — 18.

Если значения качественных или количественных признаков выражены в относительных числах (например, в процентах к об­щему числу), то эти значения именуются частостями. В этом слу­чае наши примеры выглядят так: полковников — 2%, подпол­ковников — 6, майоров — 16... всего 100%; моложе 20 лет — 4%, 20-24 года — 18, 25-29 лет — 10... всего 100%.

Ряды распределения в таблицах, как правило, имеют и час­тоты, и частости (табл. 7).

Таблица   7 Распределение сотрудников милиции по званию и возрасту

Звание	Абсолютное число	В % к итогу	Возраст, лет	Абсолютное число	В % к итогу
Полковник	1	2	До 20	2	4
Подполковник	3	6	20-24	18	36
Майор	8	16	25-29	10	20
Капитан	12	24	30-34	10	20
Ст. лейтенант	15	30	35-39	5	10
Лейтенант	10	20	40-49	3	6
Мл. лейтенант	1	2	50 и	2	4
			старше
Итого 50		100,0	Итого    50		100,0

Ряды распределения, построенные по количественному при­знаку (возраст, стаж, меры наказания, сроки расследования или рассмотрения дел, число судимостей и т. д.), называются вариа­ционными рядами. Различия единиц совокупности (до 20 лет, 20— 24 года, 25—29 лет и т. д.) количественного признака называется вариацией, а сам конкретный признак — вариантой.

Вариация признаков может быть дискретной, или прерыв­ной (20, 21, 22, 23, 24, 25 лет и т.д.), либо непрерывной (до 20 лет, 20-25, 25-30 лет и т. д.). При дискретной вариации ве­личина количественного признака (варианты) может принимать вполне определенные значения, отличающиеся в нашем при­мере на 1 год (20, 21, 22 и т.д.). При непрерывной вариации величина количественного признака у единиц совокупности в определенном численном промежутке (интервале) может при­нимать любые значения, хоть сколько-нибудь отличающиеся друг от друга. Например, в интервале 20—25 лет возраст конкретных сотрудников может быть 20 лет и 2 дня, 21 год и 10 месяцев и т. д.

Вариационные ряды, построенные по дискретно варьирую­щим признакам, именуют дискретными вариационными рядами, а построенные по непрерывно варьирующим признакам (интерва­лам) — интервальными вариационными рядами. Вариационный ряд всегда состоит из двух основных граф (колонок) цифр.

В первой колонке указываются значения количественного признака в порядке возрастания. В нашем примере интерваль­ного вариационного ряда: до 20 лет, 20-24 года, 25-29 лет и т. д. При дискретной вариации 20, 21, 22, 23, 24, 25 лет. Эти значения количественного признака и называют вариантами. В статистической литературе этот термин иногда употребляется как существительное мужского рода (вариант, варианты), а иногда — как существительное женского рода (варианта, ва­рианты).

Во второй колонке указываются числа единиц, которые свой­ственны той или иной варианте. Их называют частотами, если они выражены в абсолютных числах, т. е. сколько раз в изучае­мой совокупности встречается та или иная варианта, или часто­стями, если они выражены в удельных весах или долях, т. е. в процентах или коэффициентах к итогу.

Интервальный вариационный ряд иногда строится с равны­ми интервалами (20-24, 25-29 лет), а иногда с неравными (14-15, 16—18, 19—20, 21-25 лет) интервалами. В первом случае оба интервала равны 5 годам, а во втором случае — 2, 3, 5 годам. При построении интервального ряда с непрерывной вариацией верхняя граница каждого интервала обычно является нижней гра­ницей последующего (20-25, 25-30, 30-35 и т. д.), а в построе­нии интервального ряда по дискретному признаку границы смеж­ных интервалов не повторяются (1—5 дней, 6—10 дней, 11—15 дней и т. д.)

Статистический анализ вариационных рядов требует не только наличия частот (частостей), но и накопленных частот (частостей). Накопленная частота для той или иной варианты представляет собой сумму частот всех предшествующих вариант (интервалов). В нашем примере (таблица 7) для интервала 20-24 года накопленная частота будет равна: 2 + 18 = 20 человек, а накопленная час­тость 4 + 36 = 40%, а для интервала 25—29 лет соответственно: 2 + 18 + 10 = 30 человек, или 4 + 36 + 20 = 60%. Таким образом от варианты к варианте (от интервала к интервалу) идет накопление (кумуляция) частот и частостей.

Вариационные ряды легко изображаются графически в виде полигона или гистограммы. Графическое изображение накоплен­ных частот (частостей) воспроизводится в системе прямоуголь­ных координат в виде кумуляты, или кумулятивной кривой. По оси ординат откладывается величина накопленных частот, а по оси абсцисс — возрастающие значения количественного признака. Накопленные частоты и кумулята — это интегральные показате­ли плотности распределения в вариационном ряду.

Структурная схема обобщающих величин

Обобщающие величины

Абсолютные

Относительные

Средние

Распределения

Интенсивности

Динамики

Выполнения плана

Степени и сравнения

Индексы

Понятие рядов распределения. Дискретные и интервальные ряды распределения Рядами распределения называются группировки особого вида, при которых по каждому признаку, группе признаков или классу признаков известны численность единиц в группе либо удельный вес этой численности в общем итоге. Т.е. ряд распределения – упорядоченная совокупность значений признака, расположенных в порядке возрастания или убывания с соответствующими им весами. Ряды распределения могут быть построены или по количественному, или по атрибутивному признаку. Ряды распределения, построенные по количественному признаку, называются вариационными рядами. Они бывают дискретные и интервальные. Ряд распределения может быть построен по не прерывно варьирующему признаку (когда признак может принимать любые значения в рамках какого-либо интервала) и по дискретно варьирующему признаку (принимает строго определенные целочисленные значения).  Дискретным вариационным рядом распределения называется  ранжированная совокупность вариантов с соответствующими им частотами или частностями. Варианты дискретного ряда – это дискретно прерывно изменяющиеся значения признак, обычно это результат подсчета. Дискретные  вариационные ряды строят обычно в том случае, если значения изучаемого признака могут отличаться друг от друга не менее чем на некоторую конечную величину. В  дискретных   рядах задаются точечные значения признака. Пример: Распределение мужских костюмов, реализованных магазинами за месяц по размерам.

Размер костюма	Число проданных костюмов, шт.
44	12
46	31
48	127
50	215
52	164
54	91
56	47
58	28
60	11
Итого	726

 Интервальным вариационным рядом называется упорядоченная совокупность интервалов варьирования значений случайной величины с соответствующими частотами или частостями попаданий в каждый из них значений величины. Интервальные ряды предназначены для анализа распределения непрерывно изменяющегося признака, значение которого чаще всего регистрируется путем измерения или взвешивания. Варианты такого ряда – это группировка. Пример: Распределение покупок в продуктовом магазине по сумме.

Сумма покупки, руб.	Число покупок
До 50	37
50,1-100	78
100,1-150	111
150,1-200	105
200,1-250	68
Свыше 250	49
Итого	448

Если в дискретных вариационных рядах частотная характеристика относится непосредственно к варианту ряда, то в интервальных к группе вариантов. Ряды распределения удобно анализировать при помощи их графического изображения, позволяющего судить и о форме распределения, о закономерностях. Дискретный ряд изображается на графике в виде ломаной линии – полигона распределения. Для его построения в прямоугольной системе координат по оси абсцисс в одинаковом масштабе откладываются ранжированные (упорядоченные) значения варьирующего признака, а по оси ординат наносится шкала для выражения частот. Интервальные ряды изображаются в виде гистограмм распределения (то есть столбиков диаграмм). При построении гистограммы на оси абсцисс откладываются величины интервалов, а частоты изображаются прямоугольниками, построенными на соответствующих интервалах. Высота столбиков в случае равных интервалов должна быть пропорциональна частотам. Любая гистограмма может быть преобразована в полигон распределений, для этого необходимо соединить между собой отрезками прямой вершины ее прямоугольников. 2. Индексный метод анализа влияния средней выработки и среднесписочной численности на изменения объема продукции Индексный метод применяется для анализа динамики и сравнения обобщающих показателей, а так же факторов, влияющих на изменение уровней этих показателей. С помощью индексов можно выявить влияние средней выработки и среднесписочной численности на изменения объема продукции. Эта задача решается путем построения системы аналитических индексов. Индекс объема продукции с индексом среднесписочной численности работающих и индексом средней выработки связан таким же образом, как объем производства (Q) связан с выработкой (w) и численностью (r). Можно заключить, что объем продукции будет равняться произведению средней выработки и среднесписочной численности:  Q = w·r,                                где  Q – объем продукции,                                                                                                       w - средняя выработка,                                                     r – среднесписочная численность. Как видно, речь идет о взаимосвязи явлений в статике: произведение двух факторов дает общий объем результативного явления. Очевидно также, что эта связь функциональная, следовательно, динамика этой связи изучается с помощью индексов. Для приведенного примера это следующая система: J_w × J_r = J_wr . Например, индекс объема продукции Jwr, как индекс результативного  явления, можно разложить на два индекса-фактора: индекс средней выработки (Jw), и индекс среднесписочной численности (Jr): 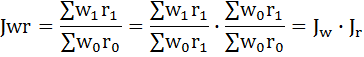              ↓                ↓              ↓                      Индекс      Индекс           Индекс                     объема       средней         среднесписочной      продукции    выработки    численности где J _w - индекс производительности труда, рассчитываемый по формуле Ласпейреса; J_r - индекс численности работающих, рассчитываемый по формуле Пааше. Индексные системы используются для определения влияния отдельных факторов на формирование уровня результативного показателя, позволяют по 2-м известным значениям индексов определить значение неизвестного. На базе приведенной системы индексов можно найти и абсолютный прирост объема продукции, разложенный на влияние факторов. 1. Общий прирост объема продукции: ∆wr = ∑w₁r₁ - ∑w₀r₀. 2. Прирост за счет действия показателя средней выработки: ∆wr/w = ∑w₁r₁ - ∑w₀r₁. 3. Прирост за счет действия показателя среднесписочной численности: ∆wr/r = ∑w₀r₁ - ∑w₀r₀ ∆wr = ∆wr/w + ∆wr/r. Пример. Известны следующие данные

Показатели	Базисный период	Отчетный период
1. средняя выработка (w)	2000	2100
2.среднесписочная численность (r)	90	100

Мы можем определить, как изменился объем продукции в относительном и абсолютном выражении и как отдельные факторы повлияли на это изменение. Объем продукции составил:     в базисном периоде     w₀  * r₀ = 2000 * 90 = 180000,     а в отчетном    w₁ * r₁ = 2100 * 100 = 210000. Следовательно, объем продукции увеличился на 30000 или на 1,16%. ∆wr=∑w₁r₁-∑w₀r₀₌(210000-180000)=30000  или (210000:180000)*100%=1,16%. Данное изменение объема продукции было обусловлено: 1) увеличением среднесписочной численности на 10 человек или на 111,1% r₁/r₀ = 100 / 90 = 1,11 или 111,1%. В абсолютном выражении за счет этого фактора объем продукции увеличился на 20000: w₀r₁ – w₀r₀ = w₀(r₁-r₀) = 2000 (100-90) = 20000. 2) увеличением средней выработки на 105% или на 10000: w₁r₁/w₀r₁ = 2100*100/2000*100 = 1,05 или 105%. В абсолютном выражении прирост составляет: w₁r₁ – w₀r₁ = (w₁-w₀)r₁ = (2100-2000)*100 = 10000. Отсюда, совместное влияние факторов составило: 1. В абсолютном выражении 10000 + 20000 = 30000 2. В относительном выражении 1,11 * 1,05 = 1,16               (116%) Следовательно, прирост составляет 1,16%. Оба результата были получены ранее. 3. Индексы постоянного состава. Принципы построения Слово «index» в переводе означает указатель, показатель. В статистике индекс трактуется как относительный показатель, характеризующий изменение явления во времени, пространстве или по сравнению с планом. Поскольку индекс относительная величина, наименования индексов созвучны с наименованием относительных величин. В тех случаях, когда мы анализируем изменение во времени сравниваемой продукции, мы можем поставить вопрос о том, как в различных условиях (на различных участках) меняются составляющие индекса (цена, физический объем, структура производства или реализации отдельных видов продукции). В связи с этим строятся индексы постоянного состава, переменного состава, структурных сдвигов. Индекс постоянного (фиксированного) состава – это индекс, который характеризует динамику средней величины при одной и той же фиксированной структуре совокупности. Принцип построения индекса постоянного состава – элиминировать влияние изменений в структуре весов на индексируемую величину путем расчета средневзвешенного уровня индексируемого показателя с одними и теми же весами. Индекс постоянного состава по своей форме тождественен агрегатному индексу. Агрегатная форма является наиболее распространенной. Индекс постоянного  состава  исчисляется с весами, зафиксированными на уровне одного какого-либо периода, и показывает изменение только индексируемой величины.  Индекс   постоянного   состава  элиминирует влияние изменений в структуре весов на индексируемую величину путем расчета средневзвешенного уровня индексируемого показателя с одними и теми же весами. В  индексах   постоянного   состава  сопоставляются показатели, рассчитанные на базе неизменной структуры явлений. При построении индексов постоянного   состава  в качестве показателя-соизмерителя используется связанный с индексируемой величиной количественный показатель. В виде примера можно привести построение индекса фиксированного состава себестоимости продукции:  =  , где  I_фс - индекс фиксированного (постоянного) состава;         z – себестоимость единицы продукции;        q – количество (объем) какого-либо товара в натуральном выражении. Для этого в качестве соизмерителя индексируемой величины – себестоимости - используется неизменный физический объем отчетного  периода. 4. Показатель прибыли от реализации товарной продукции. Методология расчета Прибыль является главным показателем эффективности работы предприятия, источником его жизнедеятельности.   Прибыль  от  реализации  товарной продукции  составляет, как правило, наибольшую часть всей балансовой прибыли  предприятия. Основными способами расчета прибыли от реализации товарной продукции являются метод прямого счета и аналитический. Метод прямого счета наиболее распространен на предприятиях в современных условиях хозяйствования. Сущность его заключается в том, что прибыль исчисляется как разница между выручкой от реализации продукции в соответствующих ценах и полной ее себестоимостью за вычетом НДС и акцизов. Если себестоимость продукции  превышает ее стоимость в оптовых ценах, то результатом производственной деятельности предприятия будет убыток. Аналитический метод применяется при большом ассортименте выпускаемой продукции, а также как дополнение к прямому методу в целях его проверки и контроля. При аналитическом методе прибыль определяется не по каждому виду выпускаемой в планируемом году продукции, а по всей сравнимой продукции в целом. Прибыль по несравнимой продукции определяется отдельно. Расчет прибыли  от  реализации  товарной продукции  может быть представлен в виде формулы: ПР = ВД - З_пр - НДС, где ВД – валовой доход (выручка) от реализации  продукции в действующих оптовых ценах; З_пр – затраты на производство и реализацию  продукции  (полная себестоимость продукции); НДС – налог на добавленную стоимость. Прибыль от реализации товарной продукции в общем случае изменяется под воздействием таких факторов, как изменение: объема реализации; структуры продукции; отпускных цен на реализованную продукцию; цен на сырье, материалы, топливо, тарифов на энергию и перевозки; уровня затрат материальных и трудовых ресурсов. 1. Расчет общего изменения прибыли ( D Р) от реализации продукции:                              D Р = Р₁ - Р₀, где Р₁ - прибыль отчетного года;            Р₀ - прибыль базисного года. 2. Расчет влияния на прибыль изменений отпускных цен на реализованную продукцию:                               D Р₁ = N_p1 - N_p1,0 = å p₁q₁ - å p₀q₁, где N_p1 = å p₁q₁ - реализация в отчетном году в ценах отчетного года (р - цена изделия; q - количество изделий); N_p1,0 = å p₀q₁ - реализация в отчетном году в ценах базисного года. 3. Расчет влияния на прибыль изменений в объеме продукции ( D Р₂) (собственно объема продукции в оценке по плановой (базовой) себестоимости): D P₂ = Р₀К₁ - Р₀ = Р₀ (К₁ - 1), где Р₀ - прибыль базисного года; К₁ - коэффициент роста объема реализации продукции; К₁ = S_1,0 / S₀, где S_1,0 - фактическая себестоимость реализованной продукции за отчетный период в ценах и тарифах базисного периода; S₀ - себестоимость базисного года (периода). 4. Расчет влияния на прибыль изменений в объеме продукции, обусловленных изменениями в структуре продукции ( D Р₃):      D Р₃ = Р₀ (К₂ - К₁), где К₂ - коэффициент роста объема реализации в оценке по отпускным ценам; К₂ = N_1,0/N₀, где N_1,0 - реализация в отчетном периоде по ценам базисного периода; N₀ - реализация в базисном периоде. 5. Расчет влияния на прибыль экономии от снижения по себестоимости продукции ( D Р₄):                                                                       D Р₄ = S_1,0 - S₁, где S_1,0 - фактическая себестоимость реализованной продукции за отчетный период в ценах и тарифах базисного периода; S₁ - фактическая себестоимость реализованной продукции отчетного периода. 6. Расчет влияния на прибыль изменений себестоимости за счет структурных сдвигов в составе продукции ( D Р₅):                D Р₅ = S₀К₂ - S_1,0. Отдельным расчетом по данным бухгалтерского учета определяется влияние на прибыль изменений цен на материалы и тарифов на услуги (D Р₆), а также экономии, вызванной нарушениями хозяйственной дисциплины (D Р₇). Сумма факторных отклонений дает общее изменение прибыли от реализации за отчетный период, что выражается следующей формулой: D Р = Р₁ - Р₀ = D Р₁ + D Р₂ + D Р₃ + D Р₄ + D Р₅ + D Р₆ + D Р₇, где D Р - общее изменение прибыли.

Вопрос№26

Вариационные ряды - это раздел математической статистики - науки о методах обработки результатов наблюдений массовых случайных явлений в социальных, экономических и технических системах.

Установление закономерностей, которым подчиняются массовые случайные явления, основано на изучении статистических данных - сведений о том, какие значения (количественные или качественные) принял в результате наблюдений признак X, который интересует исследователя.

Признак X в процессе наблюдений может принимать конкретные значения, которые обозначаются буквами латинского алфавита x_i с индексом i, указывающим его номер в ряде наблюдений, где i[1,n].

Различают дискретные и непрерывные признаки. Дискретные признаки – это признаки, которые принимают отдельные значения x_i , отличающиеся друг от друга на некоторую конкретную величину (обычно целое значение или число с одним дробным разрядом). Значения дискретного признака в ряде наблюдений могут совпадать. Различные значения признака Х называются вариантами и характеризуются частотой варианта mx. Частота варианта mx_j показывает, сколько раз встречается данное значение признака x_j в ряде наблюдений. Сумма частот вариантов равна общему количеству наблюдений признака n. По данным наблюдений за дискретным признаком строят дискретный вариационный ряд.

Непрерывные признаки - это признаки, которые принимают любые значения в некотором числовом интервале, отличаясь один от другого на сколь угодно малую величину. Количество возможных значений непрерывного признака бесконечно. Значения непрерывного признака задаются интервалами, которые характеризуются интервальной частотой m. Интервальная частота m_j показывает, сколько значений признака X принадлежит данному j-му интервалу (не выходит по значению за границы интервала). По данным наблюдений за непрерывным признаком строят интервальный вариационный ряд.

Во многих исследованиях часто имеют дело с разнообразными совокупностями вещей и явлений, которые по одним признакам представляют собой единое целое, а по другим подразделяются на отдельные группы. Такие совокупности рассматривались ранее.

     Так, в примере рассмотренном в разделе Первичная обработка результатов измерений ученики 3-го класса - это определенная совокупность элементов (учеников), представляющих собой единое целое, поскольку элементы (ученики), которые ее составляют, объединены определенным признаком - все они учатся в 3-м классе. В то же время они подразделяются на отдельные группы по другим признакам: полу, скорости чтения, успешности обучения и т. п.

     Участники областной олимпиады по математике образуют единое целое. В то же время они могут быть разделены на группы: по регионам, где они учатся; по успехам выступления на областной олимпиаде; по классам, в которых они учатся; по характеру математических способностей и т. п.

     Совокупность, состоящая из однородных элементов, имеющих качественную общность, будем называть статистической совокупностью. Элементы, из которых состоит данная совокупность, называют ее членами. Количество элементов в совокупности называют его объемом. Объем совокупности будем обозначать через n.

     Признак, по которому совокупность подразделяют на группы называют аргументом. Признак (аргумент) будем обозначать прописными латинскими буквами X, Y, Z, ... . Отдельные числовые значения аргумента называют его вариантами и обозначают через x₁, x₂, ..., x_k. (Скорость чтения - признак, его значения - x₁ = 110, x₂ = 92, ..., x₃₆ = 25.) Количество элементов совокупности, имеющих одинаковое числовое значение, мы назвали частотой данной варианты; частоты обозначили через n₁, n₂, ..., n_k; n₁ + n₂ + ... + n_k = n. Отношение частоты варианты к объему совокупности назвали относительной частотой варианты и обозначили через v₁, v₂, ..., v_k; v₁ + v₂ + ... + v_k = 1.

     В исследованиях, изучая тот или иной признак, часто приходится сталкиваться с такими совокупностями, члены которых принимают различные значения (наряду с одинаковыми). Такую переменчивость значений признака называют его варьированием. Например, варьирование мы наблюдаем, изучая успешность учащихся по предмету, сформированность некоторого качества личности и т. п.

  Если две варианты признака в данной совокупности могут отличаться одна от другой не менее чем на определенное число или вообще совпадают, то такие данные называют дискретными (число учеников в классах школы; количество баллов, которые набирает ученик при тестировании, и т. п.). Если же две варианты признака могут отличаться одна от другой на произвольно малую величину, то такие данные называют непрерывными (процент учеников, которые имеют достаточный уровень подготовки по предмету в разных классах; время, за которое ученики пробежали 60 м на соревнованиях; продолжительность работы электронных ламп; температура воздуха и т. п.).

     Ряд значений признака, или вариант, полученных вследствие массового обследования однородных вещей или явлений, размещенных в порядке возрастания или убывания их величин, вместе с соответствующими частотами (или относительными частотами) называют вариационным рядом.

     Если в вариационном ряде значения признака (варианты) заданы в виде отдельных конкретных чисел, то такой ряд называют дискретным.

     Если в вариационном ряде значения признака заданы в виде интервалов, то такой ряд называют интервальным.

     Если в интервальном вариационном ряде в двух последовательных интервалах верхнее предельное значение признака одного интервала равняется нижнему предельному значению второго, условно будем считать, что это число принадлежит второму интервалу. Разность между верхней и нижней границами интервала называют шириной этого интервала.

     Рассматриваются еще так называемые кумулятивные вариационные ряды. В таких рядах вместо частот или относительных частот определенных вариант (или интервалов) записаны накопленные частоты или относительные частоты. Например, строки 1 и 4 или 1 и 6 в таблице образуют кумулятивный вариационный ряд.

Для анализа статистических данных, содержащихся в вариационном ряде, целесообразно ввести такую числовую характеристику, как плотность распределения.

     Если в интервальном вариационном ряде ширина интервала отлична от единицы, то определяют абсолютную и относительную плотности распределения.

     Отношение частоты n_i интервала к ширине h_i этого интервала называют абсолютной плотностью распределения для i-го интервала. Будем обозначать ее символом p_i: . Абсолютная плотность распределения - это частота, приходящаяся на единицу ширины интервала. Например, по данным таблицы плотность распределения в интервале (70; 76) равна .

     Относительной плотностью распределения π_i для i-го интервала называют отношение относительной частоты интервала к его ширине: . По данным таблицы относительная плотность распределения для интервала (77; 83) равна .

Вариационный ряд – однородная в качественном отношении статистическая совокупность, отдельные единицы которой характеризуют количественные различия изучаемого признака или явления. Количественная вариация может быть двух типов: прерывная (дискретная) и непрерывная.

Прерывный (дискретный) признак выражается только целым числом и не может иметь никаких промежуточных значений (например, число посещений, численность населения участка, частота пульса, число детей в семье).

Непрерывный признак может принимать любые значения в определенных пределах, в том числе и дробные, и выражается лишь приближенно (вес, рост, АД, время).

Варианта (V) - цифровое значение каждого отдельного признака или явления, входящего в вариационный ряд. Варианты, расположенные в порядке возрастания или убывания количественной характеристики признака, составляют ранжированный вариационный ряд.

При небольшом числе наблюдений п варианты достаточно просто ранжировать. Вариационный ряд, где каждая варианта встречается лишь один раз (т. е. частоты вариант равны единице), называется простым вариационным рядом.

При увеличении числа наблюдений обычно отмечается повторение отдельных вариант. В этом случае для построения вариационного ряда необходимо выписать все значения вариант, ранжировав их, а затем подсчитать число повторений (частоту р) каждой варианты и записать их рядом с соответствующими значениями вариант.

Вариационный ряд, где указано, сколько раз встречается каждая варианта, называется сгруппированным вариационным рядом.

Главными составными элементами сгруппированного вариационного ряда являются:

V — варианты — количественные значения варьируемого признака;

р — частоты — число повторений каждой варианты;

n — общее число наблюдений (n равно сумме частот, т. е. n=Σp, где,

Сводными характеристиками значений вариант служат средняя арифметическая величина М, мода Мо и медиана Me.

Модой Мо называют значение наиболее часто встречающейся варианты.

Медианой Me — значение варианты, делящей вариационный ряд пополам (с каждой стороны медианы находится половина вариант). В редких случаях, когда имеется симметричный вариационный ряд, мода и медиана равны между собой и совпадают со значением средней арифметической. Медиана применяется в статистике сравнительно редко.

Наиболее общей характеристикой всех значений вариант является средняя арифметическая величина. При обработке вариационного ряда вычисляют среднее квадратическое отклонение и ошибку репрезентативности (погрешность), также являющиеся параметрами оценки вариационного ряда.

Вопрос№27

Перепись населения в России — сбор, обобщение, изучение и распространение демографических, экономических и социальных данных, относящихся по состоянию на определённое время ко всем лицам в России и на территории её бывших государственных образований.