Экзаменационный билет № ___6_____

1. Трубка тока и средняя по сечению скорость жидкости.

Линия тока (применяется при неустановившемся движении) – это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной.

Трубка тока - трубчатая поверхность, образуемая линиями тока с бесконечно малым поперечным сечением. Часть потока, заключенная внутри трубки тока называется элементарной струйкой(рис. 1.3).

Элементарная струйка обладает следующими свойствами:

1. форма и ориентация в пространстве элементарной струйки при установившемся движении остается неизменной во времени, в этом случае трубка тока, образованная линиями тока, с течением времени не изменяет своей формы;

2. ни одна частица жидкости не может проникнуть внутрь струйки, или выйти наружу через трубку тока, вхождения в элементарную струйку внешних линий тока не происходит, так как боковая поверхность элементарной струйки образована линиями тока, к которым скорости направлены по касательной;

3. скорости во всех точках поперечного сечения элементарной струйки можно считать одинаковыми вследствие незначительности поперечного сечения элементарной струйки.

Совокупность элементарных струек, протекающих через площадку достаточно больших (конечных) размеров, называется потоком жидкости.

Рис. 1.3. Линия тока и струйка

Рис. 1.4. Труба с переменным диаметром при постоянном расходе

Из закона сохранения вещества и постоянства расхода вытекает уравнение неразрывности течений. Представим трубу с переменным живым сечением (рис.1.4). Расход жидкости через трубу в любом ее сечении постоянен, т.е. Q₁=Q₂= const, откуда

ω₁υ₁ = ω₂υ₂

Таким образом, если течение в трубе является сплошным и неразрывным, то уравнение неразрывности примет вид:

Средняя скорость потока υ - скорость движения жидкости, определяющаяся отношением расхода жидкости Q к площади живого сечения ω

Поскольку скорость движения различных частиц жидкости отличается друг от друга, поэтому скорость движения и усредняется. В круглой трубе, например, скорость на оси трубы максимальна, тогда как у стенок трубы она равна нулю.

Основными видами движения жидкости являются: движение установившееся и неустановившееся, равномерное и неравномерное, напорное и безнапорное, сплошное и прерывистое.

Установившимся движением называется такое движение жидкости, при котором в данной точке русла давление и скорость не изменяются во времени

υ = f(x, y, z) P = φ f(x, y, z)

Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени, называется неустановившимся или нестационарным

υ = f₁(x, y, z, t) P = φ f₁(x, y, z, t)

2. Момент сил, сообщаемый потоку рабочим колесом в центробежном насосе. Основной задачей математического расчета насоса является определение его теоретического давления _t. Для определения _t рассмотрим баланс энергии между рабочим колесом и потоком. Течение жидкости между лопатками – это сложное трехмерное пространственное движение. Ввиду математической сложности точных гидродинамических уравнений полный анализ такого движения возможен только с помощью мощных компьютеров и специальных математических методов. Поэтому для упрощения задачи будем полагать, что жидкость движется по направлениям радиальной координаты и полярному углу (рис. 3.2). Это допустимо, если ширина лопастей существенно больше расстояния между ними.

Рис. 3.2.

Векторные величины впредь будем обозначать жирными буквами, скалярные  наклонными нежирными буквами.

Введем подвижную систему координат, связанную с рабочим колесом. Эта система координат вращается вместе с ним, и движется по окружности со скоростью u. Вектор скорости жидкости относительно вращающейся системы координат обозначим за w. При большом числе лопаток вектор w направлен практически по касательной к поверхности лопаток. Направление вектора u, очевидно, будет вдоль касательной к окружностям с центром оси вращения.

Скорость жидкости в неподвижной системе координат (в лабораторной системе) c получается как векторная сумма u и w:

c = u + w.

Будем параметры на входе в межлопастной канал снабжать индексом 1, а на выходе из канала  индексом 2. Тогда (рис. 3.2)

c₁ = u₁ + w₁, c₂ = u₂ + w₂.

Вектор w₂ направлен по касательной к поверхности лопатки у внешнего края рабочего колеса, и он составляет угол ₂ с направление вектора u₂.

Выделим элементарную плоскую струйку жидкости с расходом dQ. Эта струйка составлена из линии тока с близкими по величине скоростями жидкости. Найдем момент сил, действующих на элементарную струйку.

Согласно определению, дифференциал момента силы может быть определен как

dM = rdF = rdJ,

где J  скорость изменения импульса, его приращение в случае изменения массы dJ = c_dm = rc_dQ, m = dQ  скорость изменения массы. Значит,

dM = rc_dQ.

Для рассматриваемой струйки нам необходимо учесть, что в выражении для момента сил, действующих на нее, должно быть учтено только изменение момента при движении жидкости от входа и до выхода из канала. Только такое изменение связано с работой колеса. Поэтому правильное выражение имеет вид

dM = (r₂c_2  r₁c_1)dQ,

где c_1, c_2  тангенциальные составляющие векторов c₁ и c₂. Суммарный момент

.

При близко расположенных лопатках скорости c_1, c_2 практически не зависят от Q (точнее, от полярного угла, отсчитываемого вокруг оси вращения колеса). Поэтому интеграл легко вычисляется и равен

M = (r₂c_2  r₁c_1)Q.

Центробежный насос

Основным рабочим органом центробежного насоса (рис 6) является свободно вращающееся внутри корпуса колесо 1, насаженное на вал 2. Рабочее колесо состоит из двух дисков (переднего 3 и заднего 4), отстоящих на некотором расстоянии друг от друга. Между дисками, соединяя их в единую конструкцию, находятся лопасти 5, плавно изогнутые в сторону, противоположную направлению вращения колеса. Внутренние поверхности дисков и поверхности лопастей образуют так называемые межлопастные каналы колеса, которые при работе насоса заполнены перекачиваемой жидкостью.

Ротор - вал с насиженными на него вращающимися деталями - вращается в подшипниках 6. Между вращающимися и неподвижными деталями могут быть установлены уплотнения 7 для снижения утечек из насоса и уплотнения 8 для уменьшения циркуляции внутри насоса. При вращении колеса на каждую часть жидкости (массой m), находящейся в межлпастном канале на расстоянии r от оси вала и движущуюся со скоростью v , будет действовать центробежная сила:

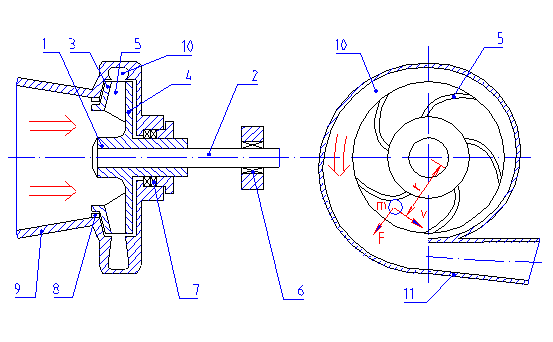  Рисунок 6. Схема центробежного насоса: 1 - колесо, 2 - вал, 3 - передний диск, 4 - задний диск, 5 - лопасти, 6 - подшипники, 7 и 8 - уплотнения, 9 - подвод, 10 - спиральный отвод, 11 - напорный патрубок. (обратно к содержанию)

Под действием этой силы жидкость выбрасывается из рабочего колеса, в результате чего в центре колеса создается разряжение, а в периферийной его части - повышенное давление. Для обеспечения непрерывного движения жидкости через насос необходимо обеспечить подвод перекачиваемой жидкости к рабочему колесу и отвод от него. Жидкость поступает через отверстие в переднем диске рабочего колеса по всасывающему трубопроводу (подводу 9). Движение жидкости по всасывающему трубопроводу происходит вследствие разности давлений над свободной поверхностью жидкости в приемном бассейне (атмосферное) и в центральной области колеса (разряжение).

Для отвода жидкости в корпусе насоса имеется расширяющаяся спиральная камера (в форме улитки, куда поступает жидкость, выбрасываемая из рабочего колеса. Спиральная камера (отвод 10) переходит в короткий диффузор, образующий напорный патрубок 11, соединяемый обычно с напорным трубопроводом.