3.3. Возможные конфигурации лопастей.

Векторы c₂, u₂ и w₂ образуют треугольник скоростей ACO (рис. 3.3). Из треугольника скоростей видно, что длина отрезка AB = AO  BO, причем AO = u₂, BO = c_2. Отсюда выразим

c_2 = u₂  AB.

В свою очередь, AB = BCctg₂ = c_2nctg₂.

Таким образом, находим

c₂cos₂ = c_2 = u₂  c_2nctg₂.

С учетом этого выражения рабочая формула для давления насоса представляется в виде

_t = u₂(u₂  c_2nctg₂). (3.3)

Из этой формулы видно, что на величину теоретического давления насоса существенно влияет угол выхода ₂ потока из рабочего колеса. Если ₂ < /2, то лопатки загнуты назад (рис. 3.4, а) к направлению вращения колеса. Давление насоса

_t < u₂².

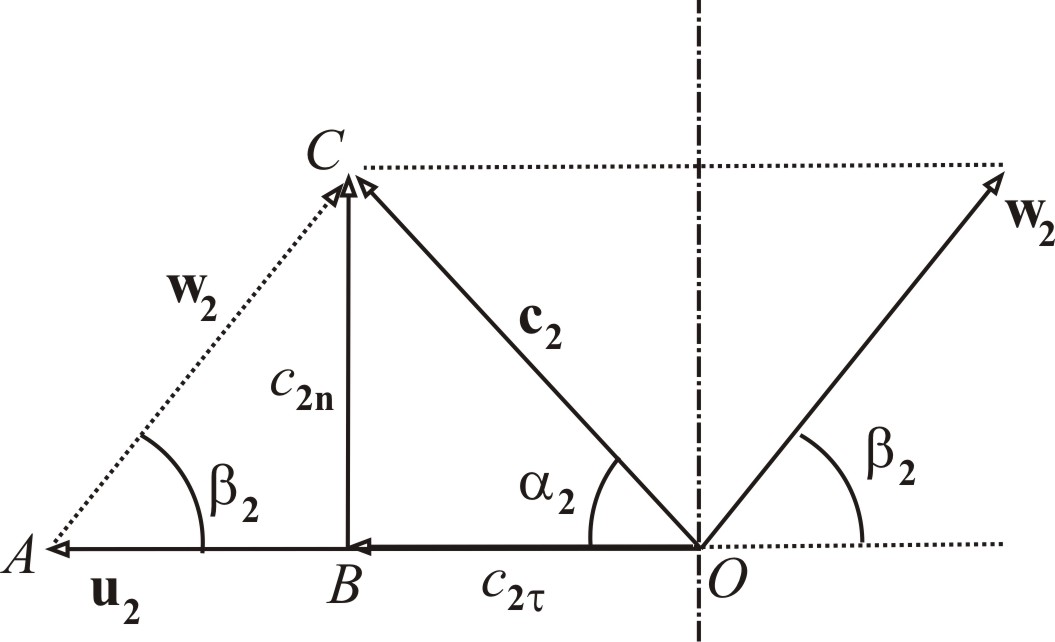
Рис. 3.3.

При ₂ = /2 (рис. 3.4, б) лопатки выбрасывают поток по направлению радиальной координаты, идущей от центра колеса. Тогда давление

_t = u₂²,

и оно больше, чем в случае, когда лопатки загнуты назад.

Если ₂ > /2 (рис. 3.4, в) лопатки загнуты вперед, и давление _t становится еще больше:

_t > u₂².

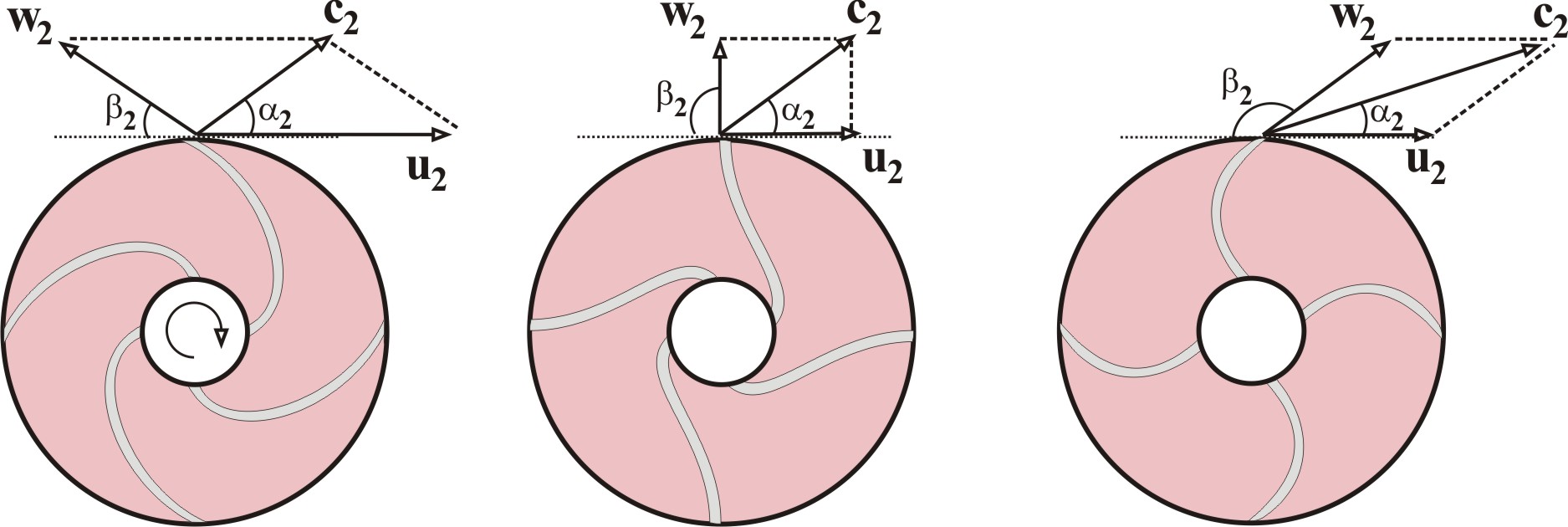
а б в

Рис. 3.4.

С технической точки зрения все три варианта вполне осуществимы. Заманчивым представляется третий случай, когда можно получать наибольшие значения _t. Однако практически целесообразным и экономически выгодным, как выяснится ниже, является насос с загнутыми назад лопатками.

2. Условие возникновения кавитации.

Возьмем, к примеру, стакан воды и поместим его в термостат, где поддерживается постоянная температура, скажем, 20 C. Если откачивать воздух из термостата, то давление в нем будет снижаться, и, наступит такой момент, когда вода в стакане начнет кипеть. Это происходит вследствие того, что давление в термостате p стало меньше давления насыщенных паров p_n при температуре T = 20 C:

. (1.1)

Давление p_n можно рассчитать по уравнению Клапейрона-Клаузиуса

,

где T_k  температура кипения при давлении p_k, L  удельная теплота парообразования, R_  газовая постоянная.

В жидкостных насосах поршень или лопасти движутся с большой скоростью, которая может быстро измениться во времени и пространстве. Например, поршень периодически меняет направление движения. Если это происходит очень быстро, то давление в месте контакта жидкости с поршнем может снизиться настолько, что выполнится неравенство (1.1). Тогда часть жидкости превратится в пар и произойдет отрыв жидкости от поршня. Или, как иногда говорят, жидкость разрывается. В последующем пар конденсируется, и образовавшаяся пустота заполняется жидкостью. Все это происходит за сотые или тысячные доли секунды. Это явление называется кавитацией. Разумеется, в газах кавитация возникнуть не может. Значение давления p зависит от устройства насосов и условий его эксплуатации

Экзаменационный билет № ___3_____

1. Условие, когда движение газа можно рассматривать в рамках гидродинамики.

Хотя газы и жидкости сильно различаются свойствами, во многих случаях их движение можно описывать одинаковым образом. Для того, чтобы механика газов и жидкостей была одинаковой, необходимо выполнения условия: перепад давления в рассматриваемой области движения должен быть незначительным. Это условие связано с поведением плотности. У газов плотность сильно зависит от давления, у жидкостей плотность очень слабо зависит от давления. Нужны относительно очень большие давления, чтобы заметным образом обнаружить изменение плотности жидкости.

Если движение газа происходит под действием небольшого перепада давления p, при котором не происходит существенного изменения  его плотности, то такое движение можно описывать теми же уравнениями, которые применяются для описания движения жидкостей. Числовым критерием такой механической неразличимости жидкостей и газов является неравенство

,

где c  скорость звука в газе.

Это не неравенство справедливо и для жидкостей. Если для жидкостей оно не выполняется, то жидкость необходимо рассматривать как газ. И в этом случае для описания движения газа необходимо применять уравнения газовой динамики.

2. Падение давления на участках с сопротивлением.