Экзаменационный билет № ___2_____

1. Треугольник скоростей в теории центробежного насоса и основные геометрические соотношения. Теоретическое давление центробежного насоса.

Основной задачей математического расчета насоса является определение его теоретического давления _t. Для определения _t рассмотрим баланс энергии между рабочим колесом и потоком. Течение жидкости между лопатками – это сложное трехмерное пространственное движение. Ввиду математической сложности точных гидродинамических уравнений полный анализ такого движения возможен только с помощью мощных компьютеров и специальных математических методов. Поэтому для упрощения задачи будем полагать, что жидкость движется по направлениям радиальной координаты и полярному углу (рис. 3.2). Это допустимо, если ширина лопастей существенно больше расстояния между ними.

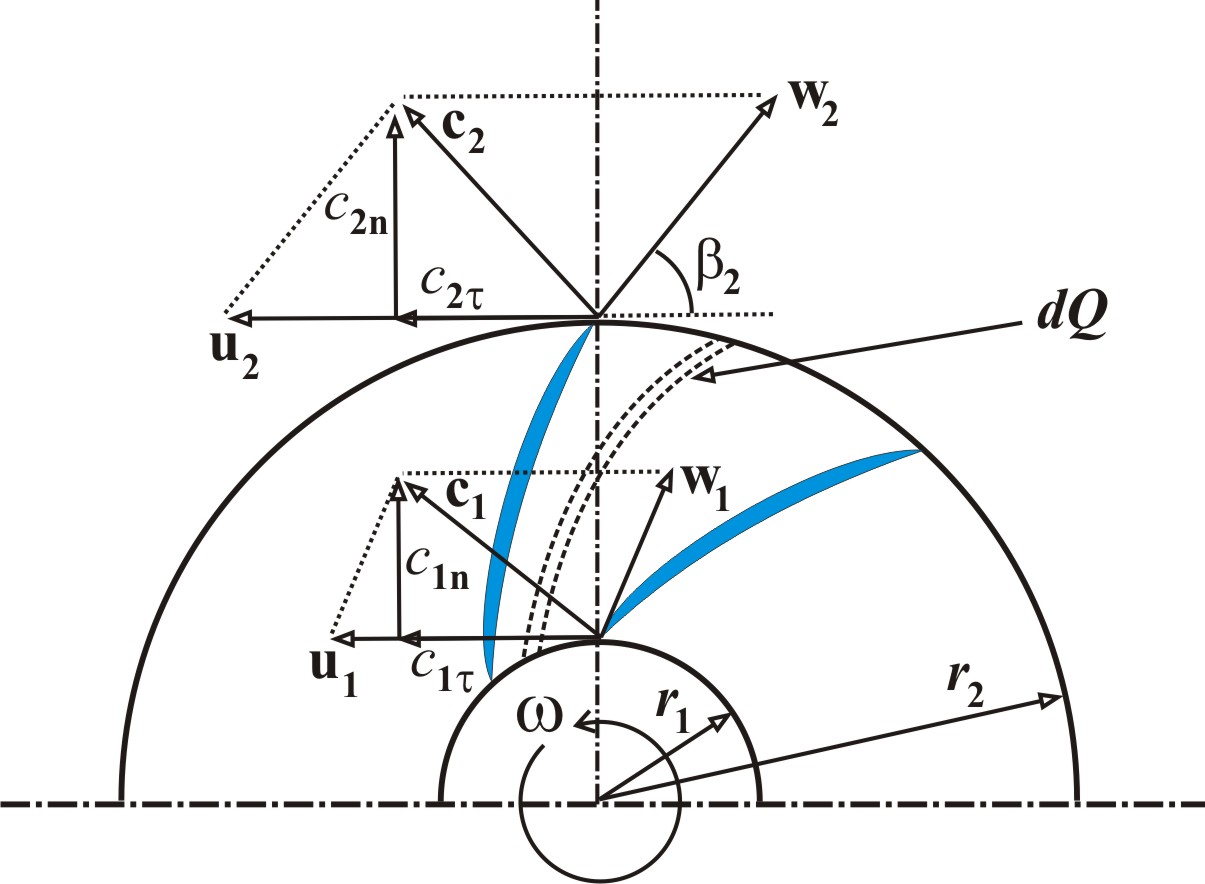
Рис. 3.2.

Векторные величины впредь будем обозначать жирными буквами, скалярные  наклонными нежирными буквами.

Введем подвижную систему координат, связанную с рабочим колесом. Эта система координат вращается вместе с ним, и движется по окружности со скоростью u. Вектор скорости жидкости относительно вращающейся системы координат обозначим за w. При большом числе лопаток вектор w направлен практически по касательной к поверхности лопаток. Направление вектора u, очевидно, будет вдоль касательной к окружностям с центром оси вращения.

Скорость жидкости в неподвижной системе координат (в лабораторной системе) c получается как векторная сумма u и w:

c = u + w.

Будем параметры на входе в межлопастной канал снабжать индексом 1, а на выходе из канала  индексом 2. Тогда (рис. 3.2)

c₁ = u₁ + w₁, c₂ = u₂ + w₂.

Вектор w₂ направлен по касательной к поверхности лопатки у внешнего края рабочего колеса, и он составляет угол ₂ с направление вектора u₂.

Выделим элементарную плоскую струйку жидкости с расходом dQ. Эта струйка составлена из линии тока с близкими по величине скоростями жидкости. Найдем момент сил, действующих на элементарную струйку.

Согласно определению, дифференциал момента силы может быть определен как

dM = rdF = rdJ,

где J  скорость изменения импульса, его приращение в случае изменения массы dJ = c_dm = rc_dQ, m = dQ  скорость изменения массы. Значит,

dM = rc_dQ.

Для рассматриваемой струйки нам необходимо учесть, что в выражении для момента сил, действующих на нее, должно быть учтено только изменение момента при движении жидкости от входа и до выхода из канала. Только такое изменение связано с работой колеса. Поэтому правильное выражение имеет вид

dM = (r₂c_2  r₁c_1)dQ,

где c_1, c_2  тангенциальные составляющие векторов c₁ и c₂. Суммарный момент

.

При близко расположенных лопатках скорости c_1, c_2 практически не зависят от Q (точнее, от полярного угла, отсчитываемого вокруг оси вращения колеса). Поэтому интеграл легко вычисляется и равен

M = (r₂c_2  r₁c_1)Q.

Умножив обе части на частоту , получим мощность, сообщаемую потоку жидкости рабочим колесом  т.н. гидравлическую мощность W_g = M:

W_g = (r₂c_2  r₁c_1)Q = (u₂c_2  u₁c_1)Q. (3.1)

Выражение (3.1) называется основным уравнением лопастных машин. Оно остается справедливым также и для осевых нагнетателей.

Здесь учтено, что на входе в межлопастные каналы скорость u₁ = r₁, на выходе u₂ = r₂.

Как мы знаем, давление насоса связано с удельной энергией жидкости. Эта связь

. (3.2)

Индекс t означает, что _t  теоретическое давление.

При выводе формулы (3.2) не учитывались гидравлические потери в насосе за счет сил трения, линии тока в межлопастном канале полагались идентичными друг другу. Эти факторы дают заниженное значение реального давления насоса, по сравнению с вычисляемым значением по формуле (3.2).

Формулу (3.2) можно еще записать как

,

где ₁, ₂  углы между векторами c и u на входе и выходе из рабочего колеса.

В практике изготовления насосов кривизна лопаток выбирается так, чтобы ₁ = 90 (cos₁ = 0). Тогда

. (3.3)

Формула (3.3) является базовой для получения основного уравнения центробежного (лопастного) насоса.