Экзаменационный билет № __1__
1. Разновидности промышленных нагнетателей и принципы их работы.
Машины для подачи газовых сред в зависимости от развиваемого ими давления называют вентиляторами, газодувками и компрессорами. Причем они характеризуются степенью повышения давления отношение давления на выходе из машины к давлению на ее входе. Основная суть из действия, как и насосов, заключается в превращении работы двигателя в кинетическую и потенциальную энергию потока жидкости или газа.
Вентилятор – машина, перемещающая газовую среду при степени повышения давления до 1,15.
Газодувка – машина, работающая при 1,15 3. Она искусственно не охлаждается из-за незначительно нагрева газа.
Компрессор сжимает газ при > 3 и имеет обычно искусственное (чаще водяное) охлаждение камер, где происходит сжатие газа.
Насосы по принципу действия подразделяются на два основных класса: динамические и объемные.
В объемных насосах энергия передается жидкой среде в рабочих камерах, в которых рабочее пространство с жидкостью периодически меняет объем. Т.е. подача жидкости происходит с перерывами. Камера попеременно сообщается с входом и выходом насоса. Для этого класса типичными являются поршневой и роторный насос.
В динамических насосах превращение работы двигателя потоку жидкости происходит под влиянием сил, действующих на жидкость в рабочих полостях, постоянно соединенных с выходом и входом насоса. В отличие от объемных машин здесь поток перекачиваемой жидкости непрерывен.
Типичным представителем таких машин является центробежный насос.
Упрощенная и краткая классификация машин для подачи жидкостей и газов на основе конструктивных признаков и свойств перемещаемой среды приведена ниже на рисунке.
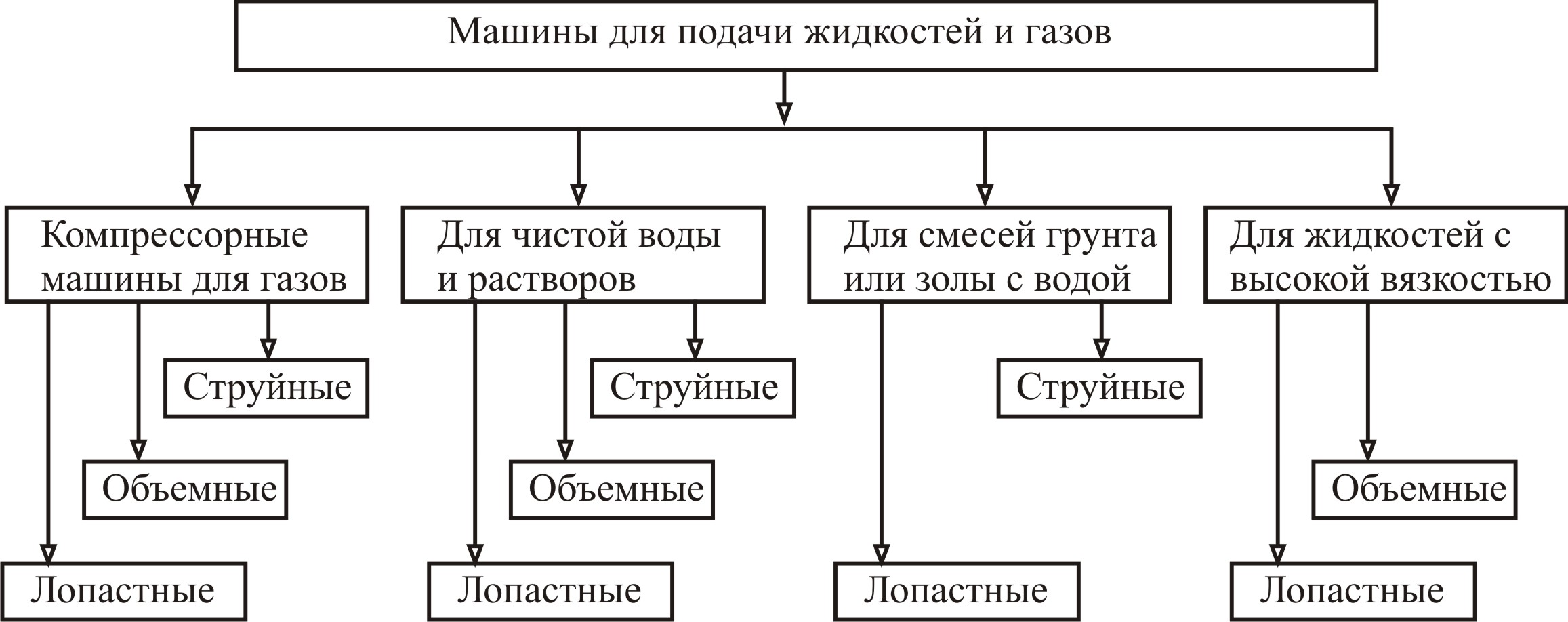
2. Основные понятия и законы движения жидкостей и газов.
Т.к. насосы, вентиляторы и компрессоры предназначены для приведения в движение жидкостей и газов, то ознакомимся с основными законами движения таких сред. Они необходимы для понимания принципов работы указанных технических устройств. Кроме того, знание технических деталей необходимы для проведения расчетов по их проектированию насосы, вентиляторы и компрессоры, при выборе технических показателей при установке на промышленных объектах.
Из курса физики известны три закона Ньютона. Зная и умея применять их на практике, можно решить любую задачу о движении твердого тела или материальной точки. Но в отличие от таких объектов жидкости и газы обладают свойством текучести, что привносит существенные математические сложности при описании их движения.
Законы Ньютона фундаментальны, они в целом справедливы к любым объектам. Но применительно к текучим средам (сплошным средам) обретают другую математическую форму. Дело в том, что в сплошной среде сколь угодно малая частица тесно взаимодействует с другими такими же частицами, которых очень много.
Перечислим основные физические понятия, которые нам понадобятся в дальнейшем.
Плотность.
В механике сплошных сред не рассматривается каждая материальная частица (атом или молекула), ее масса и объем. Вместо них сразу берется множество частиц, которое называют частицей среды. Ее конкретные размеры не имеют значения, главное, чтобы внутри частицы среды такие параметры, как плотность, давление, температура и т.д. оставались неизменными по пространству. Так что частица среды характеризуется не массой, например, плотностью , кг/м3.
Вязкость и напряжения.
Внутри сплошных сред (твердых тел, гелей, жидкостей и газов, насыпных масс и т.д.) при их деформации присутствует внутреннее трение. Поясним его природу на примере жидкости. Пусть между двумя достаточно большими квадратными пластинами размером и площадью S = LL (рис. 1) имеется тонкий слой y жидкости (y/L << 1). Если попытаться двигать верхнюю пластину с постоянной скоростью V, то окажется, что это возможно только при приложении к этой пластине определенной силы Fc. Причем, повторяя опыт с различными размерами пластин, толщинами слоя и разновидностями жидкости, обнаружим, что
вместе с пластиной в движение приходит и жидкость между пластинами, причем ее скорость распределяется неравномерно по толщине слоя y;
в непосредственной близости к нижней неподвижной пластине скорость жидкости равна нулю, а вблизи верхней пластины равна V;
величина прилагаемой силы Fc зависит от площади пластин, скорости V и природы жидкости.
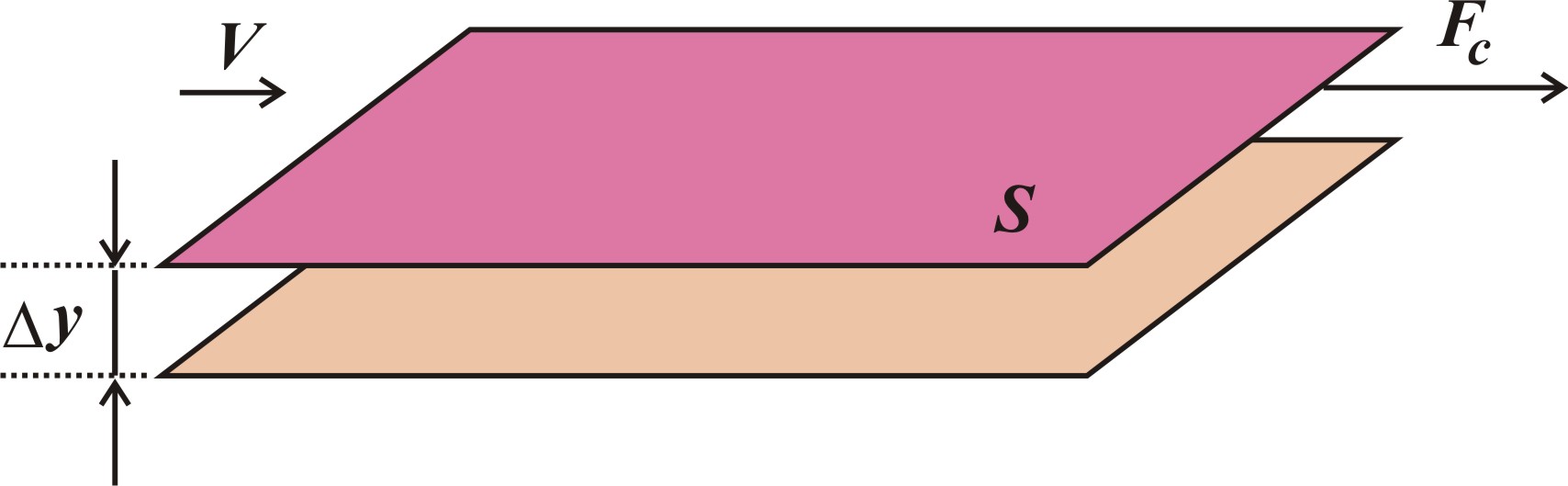
Рис. 1.1.
Таким образом, в результате множества опытов убеждаемся, что
,
где новая константа характеризует свойство жидкости, она называется кинематической вязкостью. Произведение = получило название динамической вязкости.
Вместо силы удобно ввести удельную величину = Fc/L2 = Fc/S, называемую касательным напряжением. Тогда результаты опытов можно подытожить зависимостью
.
Здесь отношение V/y на самом деле является производной скорости жидкости dv/dy, поэтому более строгая математическая формулировка полученного результата выглядит как
.
Эта формула носит название закона трения Ньютона. Ее правая часть имеет размерность давления. В механике сплошных сред такие величины называются касательными напряжениями. Такие напряжения существуют между любыми, движущимися с различными скоростями слоями жидкости. Касательные напряжения выражают силы внутреннего трения в сплошных средах.
Давление.
Движение жидкости или газа может быть вызвано или внешними силами, или перепадом давления между различными участками среды, или ими вместе одновременно. Но, как правило, в движущейся среде всегда существует перепад давления. В механике сплошных сред касательные напряжения и давление объединяются в одну общую величину – тензор напряжений :
.
Здесь p давление, xy, xz, … касательные напряжения. С одной из них мы уже ознакомились выше. Если взять частицу жидкости в виде куба, то по нормали к граням куба будут действовать давление, а вдоль граней касательные напряжения. Согласно третьему закону Ньютона действие равно противодействию. Т.к. касательные напряжения, в сущности, силы (трения), то xy = yx, xz = zx, yz = zy. Т.е. элементы, симметрично расположенные относительно главной диагонали, равны между собой.