3.3. Оптимальное комплектование машин в условиях неполной

определенности о среде

Оптимальное комплектование машин в условиях неполной определен­ности о среде проводится в соответствии с теорией игр и статистических решений. В этих условиях требуется принять оптимальное решение или близкое к нему, т.е. определить такие параметры комплекта машин, кото­рые обеспечивают максимальную эффективность его использования.

Постановка задачи и выбор критерия оптимизации. Допустим, что для строительства некоторого объекта можно использовать несколько раз­личных комплектов машин. .Допустим также, что извест­ны все возможные условия предстоящей работы их и из­вестны затраты каждого возможного варианта комплекта машин при раз­личных условиях работы – у1.Вся необходимая информация представляется в виде матрицы затрат (табл. 3.S). Требуется найти такой вариант комплекта машин, который минимизирует средние затраты:

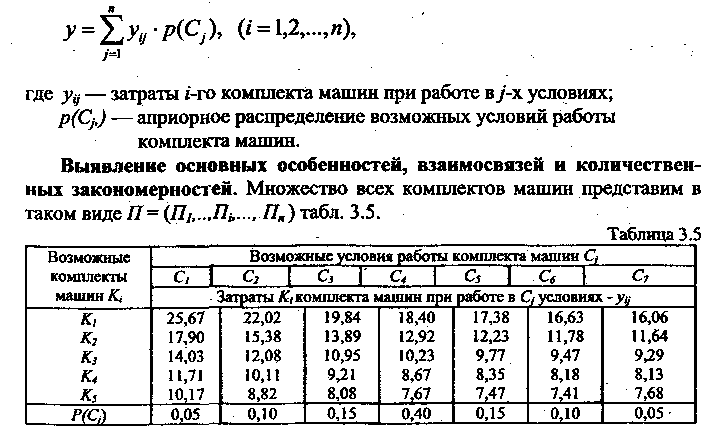
Минимальные затраты для априорного распределения условий работы соответствуют использованию 5-го комплекта машин.

Часто проектировщик может иметь некоторую информацию о среде, будущих условиях работы комплекта машин или интуитивно догадываться о них. Все это накладывает определенную специфику на процесс формиро­вания оптимального комплекта машин. В этом случае проектировщик име­ет дело с априорной информацией и может быть использован байесовский подход, который состоит в определении и использовании априорных веро­ятностей событий для расчета апостериорных вероятностей:

Те комплекты машин, которые обеспечат минимальные значения кри­терию оптимизации, и будут искомыми.

Исследование математической модели. Алгоритм расчета включает следующие основные этапы:

1. Вычисление ожидаемых затрат для каждого варианта комплекта машин П_ь (i=I, 2, ..., п), используя априорное распределение.

2. Выбор из всех комплектов машин того, который обеспечил мини­мальные затраты. Если проектировщик не располагает дополнительной информацией, то расчет на этом заканчивается. При наличии дополнитель­ной информации по тем или иным возможным условиям работы комплекта машин переходят к следующему этапу.

3. Определение апостериорных вероятностей распределения p(Cj/ п-j по формуле Байеса.

Вычисление ожидаемых затрат для каждого варианта комплекта машин

используя апостериорное распределение.

5. Выбор из всех комплектов машин того, который обеспечил мини­мальные затраты.

Для снижения трудоемкости определения оптимального комплекта ма­шин в условиях неполной определенности целесообразно использовать электронно-вычислительную технику, которая не только снижает трудоем­кость требуемых вычислений, но и резко сокращает время поиска. Ниже приводится соответствующая программа, написанная на языке ФОРТРАН, позволяющая эффективно определять оптимальный комплект машин (прогр. 3).

Программа в представленном виде допускает возможность просчета до 20 различных вариантов комплектов машин и до 9 возможных состояний среды. При необходимости эти ограничения можно изменить, введя соот­ветствующие изменения в операторе DIMENSION.

Для численного примера расчета, в качестве условного распределения для возможных работ комплекта машин, взято нормальное распределение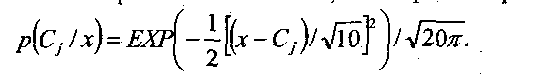

Ниже приводится программа, написанная на языке программирования Фортран, для определения оптимального комплекта машин в условиях неоп­ределенности с и без исходной информации о среде (прогр. 3.3).

В результате расчета на печать выводятся:

- апостериорное распределение параметра среды;

- ожидаемые затраты для каждого варианта с априорным распределением па­раметра среды;

- минимальные затраты с априорным распределением параметра среды;

- оптимальная система машин с априорным распределением параметра среды;

- ожидаемые затраты для каждого варианта с апостериорным распределением

параметра среды;

- минимальные затраты с апостериорным распределением параметра среды;

- оптимальная система машин с апостериорным распределением параметра

среды.

Результаты расчета.

ПРОГРАММА NEOP.FOR

ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОЙ СИСТЕМЫ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ С И БЕЗ

ИСХОДНОЙ ИНФОРМАЦИИ О СРЕДЕ ВХОДНЫЕ ПАРАМЕТРЫ NF-ПРИЗНАК НАЛИЧИЯ ИСХОДНОЙ ИНФОРМ.О СРЕДЕ

NF=0 ИНФОРМАЦИЯ ОТСУТСТВУЕТ: NF=l ИМЕЕТСЯ М-ЧИСЛО ВАРИАНТОВ СИСТЕМЫ ДО 20 N-ЧИСЛО ВОЗМОЖНЫХ СОСТОЯНИЙ СРЕДЫ ДО 8 А(I,J)-ЗАТРАТЫ 1-Й СИСТЕМЫ В J-M СОСТ.СРЕДЫ Р(Л-ВЕРОЯТН.НАХОЖДЕНИЯ СРЕДЫ В СОСТОЯНИЕ J TH(J)-СЛУЧ.ЗНАЧЕНИЕ ПАРАМЕТРА СРЕДЫ Е СОСТ.J ХМ-МАТЕКАТИЧЕСКОЕ ОЖИДАНИЕ ПАРАМЕТРА СРЕДЫ D-ДИСПЕРСИЯ ПАРАМЕТРА СРЕДЫ

ВЫХОДНЫЕ ПАРАМЕТРЫ

NT(J) - АПОСТЕРИОРНОЕ РАСПР.ПАРАМЕТРА СРЕДЫ .03 .09 .16 .44 .16 .09 .03

ELIH - ОЖИДАЕМЫЕ ЗАТРАТЫ КАЖДОГО ВАРИАНТА С АПРИОРНЫМ РАСПРЕДЕЛЕНИЕМ ПАРАМЕТРА СРЕДЫ 18.89 13.27 10.52 S.93 7.ЭО SM - МИНИМАЛЬНЫЕ ЗАТРАТЫ С АПРИОРНЫМ РАСПРЕ -

ДЕЛЕНИЕМ ПАРАМЕТРА СРЕДЫ РАВНЫ 7.90 IM - ОПТИМАЛЬНАЯ СИСТЕМА МАШИН С (5) ELP(I) - ОЖИД. ЗАТРАТЫ ВАРИАНТА С АПОСТЕРИОРНЫМ

РАСПРЕДЕЛЕНИЕМ ПАРАМЕТРА СРЕДЫ РАВНЫ 18.80 13.21 I0.47 8.88 71.86 SMР - МИНИМАЛЬНЫЕ ОЖИДАЕМЫЕ ЗАТРАТЫ С АПОСТЕР.

РАСПРЕДЕЛЕНИЕМ ПАРАМЕТРА СРЕДЫ РАВНЫ 7.86 INР - ОПТИМАЛЬНАЯ СИСТЕМА МАШИН С(5)