Глава 3. Формирование оптимальных комплектов и комплексов машин

3.1. Оптимальное комплектование машин в условиях полной определенности

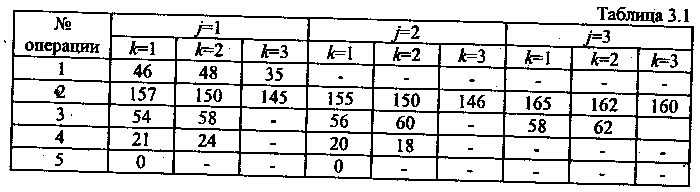
Постановка задачи и выбор критерия оптимизации. Пусть задан не­который технологический процесс, включающий, а операций. Каждая опе­рация может быть выполнена различными типами и типоразмерами машин. Известны приведенные затраты на выполнение каждой операции каждой машиной. Исходная информация, необходимая для формирования опти­мального комплекса машин, представлена в табл. 3.1

Требуется сформировать такой комплекс машин, т.е. на каждой опера­ции выбрать такие машины, которые обеспечивают минимальные приве­денные затраты на выполнение всего технологического процесса.

Выявление основных особенностей, взаимосвязей и количествен­ных закономерностей. Изобразим графически все возможные комплексы машин в виде сетевого графа. Каждая операция в сетевом графе (рис. 3.1) представляется в виде стрелки с указанием над ней приведенных затрат на выполнения i-й операции к-й машиной после выполнения у'-й машиной (i -/)-й операции.

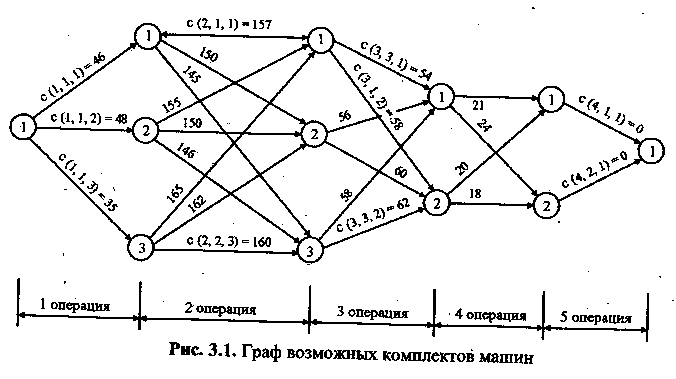
Стрелка означает также возможные связи одной машины с другими. Кружочек означает завершение одной операции одним типом машин и на­чало выполнения другой операции другим типом машин.

Число, стоящее в кружочке, означает номер (тип, типоразмер) машины, используемой на предшествующей операции. Число над кружочком означа­ет сквозную нумерацию машин, определяющих допустимое множество машин, для выполнения, данного технологического процесса. Начальный и конечный кружочки сетевого графа означают, соответственно, начало вы­полнения технологического процесса и его завершение, а номера над ними (0 и 11 — номера фиктивных машин). Таким образом, в нашей задаче для формирования оптимального комплекса машин принято 10 машин. Из них по три типа, (типоразмера) на 1-й и 2-й операциях и по два На 3-й и 4-й опе­рациях.

Приведенные затраты C(iJ,k) на выполнение (-ой операции А-ой маши­ной после выполнения у'- ой машиной (i -1)-ой операции даны в табл. 3.1.

Если при выполнении какой-то операции, например транспортировки продукции, габариты и грузоподъемность транспортного средства не соот­ветствуют параметрам погрузочного оборудования, то в этих условиях дан­ное погрузочное оборудование не может быть использовано с данным по­грузочным средством. В этом случае на графе возможных комплексов ма­шин должна отсутствовать связь (стрелка) между этими машинами. Мно­жество такого рода ограничений часто упрощает решение задачи при ис­пользовании специальных методов решения.

Представление всех возможных комплексов машин в виде графа обес­печивает наглядность и простоту формирования допустимого множества.

Данная задача относится к классу комбинаторных, в которых число воз­можных комплексов N = З^шЗ*2*2 = 36.

При увеличении операций и машин на каждой операции резко возрас­тает число возможных комплексов.

Построение математической модели. Для решения данной задачи воспользуемся принципом оптимальности Беллмана (метод динамического программирования), согласно которому оптимальный выбор обладает тем свойством, что, каковы бы ни были первоначальное состояние и решение в начальный момент, последующие решения должны быть оптимальными.

Метод динамического программирования дает возможность заменить перебор всех вариантов определенной системой действий, при которых отыскание экстремума многих переменных заменяется многократным оты­сканием экстремума функции одиой переменной. Оптимизируемый процесс разделяется на ряд последовательных этапов (шагов). Затем проводится последовательная оптимизация на каждом шаге. В качестве математиче­ской модели может быть использовано функциональное уравнение Беллма­на, которое дает ключ для решения задачи:

где y(i, j) —- минимальные приведенные затраты для комплекса машин, вы­полняющего технологический процесс, начиная с i-й операции и с_/-й машины;

y(i+l,k) — то же,¹ начиная с (i+I)-& операции и с 4-й машины.

Исследование математической модели. Алгоритм оптимизации вы­бора оптимального комплекса машин методом динамического программи­рования состоит из двух основных этапов..

На первом этапе производят расчет критерия оптимизации, для частич­ных комплексов машин начиная с машин, выполняющих последнюю опе­рацию. Постепенно переходя к началу технологического процесса и ис­пользуя функциональное (рекуррентное) уравнение Беллмана, определяют минимальные приведенные затраты.

На первом шаге полагают

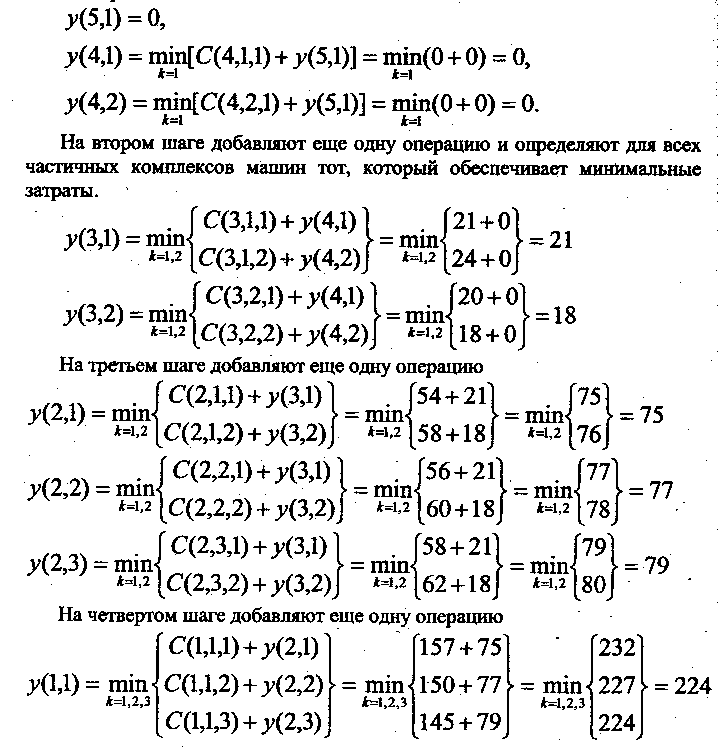
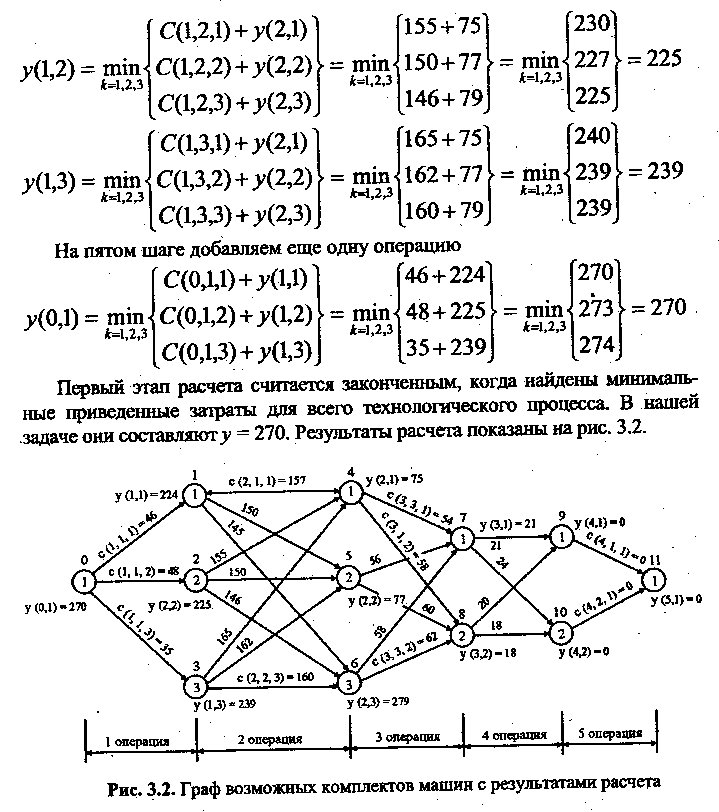
Минимальные значения критерия оптимизации для частичных ком­плексов машин y(i,j) представлены рядом с кружочками.

После этого переходят ко второму этапу, на котором определяются именно те машины, которые обеспечили минимум выбранному критерию

оптимизации.

На втором этапе, который выполняется в обратной последовательности, на каждом шаге определяется машина, затраты от которой вошли в сум­марный минимум критерия оптимизации. Так, в нашей задаче на четвертом шаге в состав комплекса машин вошла машина М(1, 1), на третьем М(2, 3), на втором М(3, 1); на первом М(4, 1). Таким образом, в оптимальный ком­плект машин вошли следующие машины:

Если ввести сквозную нумерацию машин (см. рис. 3.2) (числа над кру­жочками), то в оптимальный комплект машин войдут следующие машины:

Для снижения трудоемкости определения оптимального комплекта ма­шин в условиях полной определенности целесообразно использовать элек­тронно-вычислительную технику, которая не только снижает трудоемкость требуемых вычислений, но и резко сокращает время поиска.

Ниже приводится программа, написанная на языке программирования Фортран, для определения оптимального комплекта машин в условиях полной определенности методом Беллмана (прогр. 3.1).

В результате расчета на печать выводятся: оптимальный комплект машин и минимальные суммарные затраты, связанные с работой оптимального комплекта машин.

Программа в представленном виде допускает возможность просчета до 7 операций в технологическом процессе с числом возможных вариантов ма­шин на каждой операции до 8. При необходимости эти ограничения можно изменить, введя соответствующие изменения в операторе DIMENSION.