103. Насыщение фронта работ комплектами машин

С увеличением числа используемых комплектов машин на объекте, с одной стороны, возрастают прямые затраты: единовременные в связи с уве­личением затрат на частые перебазировки, монтаж и демонтаж техники, из-за уменьшения числа смен работы техники в году, с другой стороны, воз­растает экономический эффект от досрочного ввода объекта в строй.

Рассмотрим один из методов определения оптимального насыщения фронта работ комплектами машин.

Постановка задачи и выбор критерия оптимизации. Определить оп­тимальное число комплектов машин и оптимальный комплект машин, на­пример, по главному параметру - производительности, чтобы суммарные приведенные затраты на выполнение заданного объема работ с учетом эф­фекта от досрочного ввода объекта в строй были минимальные.

На стадии предварительного расчета и при отсутствии исходных дан­ных о прибыли от строительства того или иного объекта допускается опре­деление экономического эффекта по формуле

Выявление основных особенностей, взаимосвязей и количествен­ных закономерностей. В качестве искомых параметров примем число не­обходимых комплектов машин и главный параметр комплекта машин -производительность, который, во - первых, определяет возможности ком­плекта машин, а во - вторых, в наибольшей степени влияет на технико-экономические показатели работы комплекта машин. Главным параметром комплекта машин может быть некоторый синтезированный показатель, на­пример, производительность комплекта машин.

Выразим отдельные составляющие критерия оптимизации в функции искомых параметров. Примем в качестве искомых параметров число ком­плектов машин и, а в качестве главного параметра комплекта машин • его техническую производительность 77.

Выразим отдельные составляющие критерия оптимизации в функции искомых параметров. Тогда себестоимость механизированных работ можно представить в таком виде

Отдельные составляющие себестоимости машино-смены и капиталь­ные вложения на приобретение комплекта машин статистически связаны с искомым параметром — производительностью комплекта машин.

При установлении необходимых статистических" связей ограничимся аппроксимациями этих связей уравнениями регрессии линейного вида. Это, во-первых, всегда возможно для некоторого интервала изменения искомого параметра, а во-вторых, можно так подобрать интервалы изменения иско­мого параметра во всем диапазоне его изменения, что в этих интервалах связи будут описываться уравнениями линейного вида. Это позволяет зна­чительно упростить задачу поиска оптимального решения на отдельном (локальном) замкнутом интервале изменения искомого параметра и стан­дартизировать отыскание глобального оптимума на всем интервале исследования искомого параметра. Последнее заключается в сравнении результа­тов исследования в локальных интервалах исследования и выбор из них того, которому соответствует минимальное значение целевой функции.

При использовании данного метода выразим необходимые связи в та­ком виде:

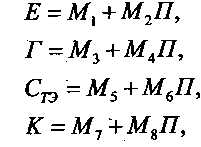
где M1 и M8 — свободные члены и коэффициенты уравнений регрессии.

Построение математическое модели. На этом этапе выразим крите­рий оптимизации - приведенные затраты с учетом эффекта от досрочного ввода объекта в строй в функции искомых параметров. Для этого подставим в исходное выражение критерия оптимизации все аналитические выраже­ния, полученные на втором этапе. Математическая модель после некоторых преобразований будет выглядеть так:

Для упрощения выкладок в качестве критерия оптимизации примем удельные затраты. Для этого разделим все члены целевой функции на объ­ем работ на объекте

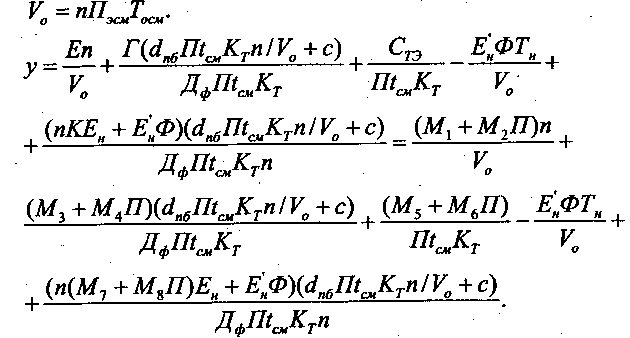
Аналогичная математическая модель получается и для выражения кри­терия оптимизации, в котором учитывается прибыль, получаемая от дос­рочного ввода объекта в строй.

Исследование математической модели. Для определения оптималь­ного числа комплектов машин на объекте и оптимальной производительно­сти комплекта необходимо взять первые частные производные по искомым параметрам. Полученные при этом выражения необходимо приравнять к нулю и решить полученную систему уравнений.

Решая полученную систему уравнений, найдем аналитические выражения для определения оптимальных значении искомых параметров:

Анализируя полученную систему аналитических выражений для определе­ния оптимального числа комплектов машин и оптимальной производитель­ности, можно отметить, что с увеличением числа дней на перебазирование комплекта машин как число комплектов машин на объекте, так и произво­дительность комплекта машин уменьшаются.

Далее, чем больше объем работ, выполняемый на объекте, тем больше требуется комплектов машин с большей производительностью, обеспечи­вающих минимальные удельные приведенные затраты с учетом эффекта от досрочного ввода объекта в строй.

Одновременно с этим можно отметить, что с увеличением стоимости фондов, вводимых в строй, число комплектов машин и их производитель­ность возрастают.

Для решения полученной системы аналитических выражений может быть использован как графический метод решения системы уравнений, так и метод последовательных приближений, позволяющий найти искомое ре­шение после 3...4 итераций.

Для определения оптимального числа комплектов машин и оптималь­ной производительности, требуется произвести большой объем вычисле­ний. Для эффективного выполнения необходимых расчетов целесообразно иметь соответствующее программное обеспечение. Ниже представлена ФОРТРАН-программа (прогр. 10.1)