10.2. Оптимизация структуры системы обслуживания

Постановка задачи и выбор критерия оптимизации. Допустим, что в механизированном подразделении имеются средства механизации, для ко­торых известна интенсивность потока отказов >. и интенсивность устране­ния отказа ц с помощью некоторой системы обслуживания. Требуется оп­ределить, какое число обслуживаемых машин должно быть прикреплено к средству обслуживания или, что то же самое, сколько машин должно об­служивать средство обслуживания, чтобы получить максимальный эффект.

В качестве критерия оптимизации примем удельные приведенные за­траты с учетом эффекта, получаемого от досрочного ввода объекта в строй, связанные с работой и простоем средств механизации и их обслуживания. Критерий оптимизации можно представить в таком виде.

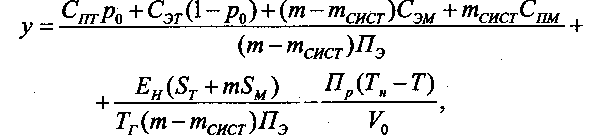
Выявление основных особенностей, взаимосвязей и количествен­ных закономерностей. Для определения оптимального числа обслуживае­мых средств механизации (машин) необходимо рассмотреть вероятностный процесс выхода из строя машин и их обслуживание. В большинстве таких ситуаций мы имеем дело с простейшим потоком отказов и простейшим по­током обслуживания средств механизации.

При оптимизации ТО средств механизации можно высказать три гипо­тезы: потоки выхода из строя машин и их обслуживания стационарны, ор­динарны и в них отсутствует последействие. Вообще, если рассматривать работу машины в течение всего срока службы, то поток выхода из строя машины не стационарен. Интенсивность его, как правило, возрастает с уве­личением срока службы средства механизации. Однако для некоторого ин­тервала времени процесс можно считать вполне стационарным.

Свойство ординарности потока, как правило, выполняется, т. е. вероят­ность поступления двух и более машин на обслуживание в один момент времени равна нулю или имеет столь малую величину, что ею можно пре­небречь. Отсутствие последействия проявляется в том, что вероятность по­ступления машин на обслуживание в некоторый момент времени не зависит от того, сколько уже машин поступило на обслуживание, т. е. вероятность отказа машины не зависит от того, отказала или нет другая машина.

Поток машин (требований), удовлетворяющий трем вышеперечислен­ным гипотезам, как мы уже знаем, называется простейшим. Простейший поток называют также стационарным пуассоновским потоком. В большин­стве задач замена не пуассоновских потоков пуассоновскими с теми же интенсивностями приводит к получению решения, которое мало отличается от истинного, а иногда и вовсе не отличается.

В качестве простого критерия небольшого отличия реального стацио­нарного потока от пуассоновского можно рассматривать близость матема­тического ожидания и дисперсии числа событий, поступающих на опреде­ленном участке времени в реальном потоке. А мы уже знаем, что если по­токи событий пуассоновские, то функционирование таких "систем может быть описано системой обыкновенных дифференциальных уравнений.

Для составления системы обыкновенных дифференциальных уравнений необходимо сначала составить размеченный граф состояний {рис. 10.2).

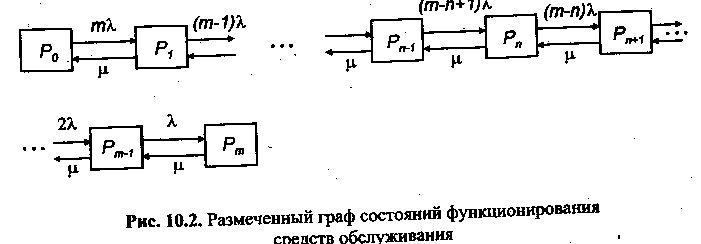
В соответствии с размеченным графом состояний, используя мнемони­ческое правило, напишем систему обыкновенных дифференциальных уравнений, описывающих функционирование средств механизации и обслужи­вания их:

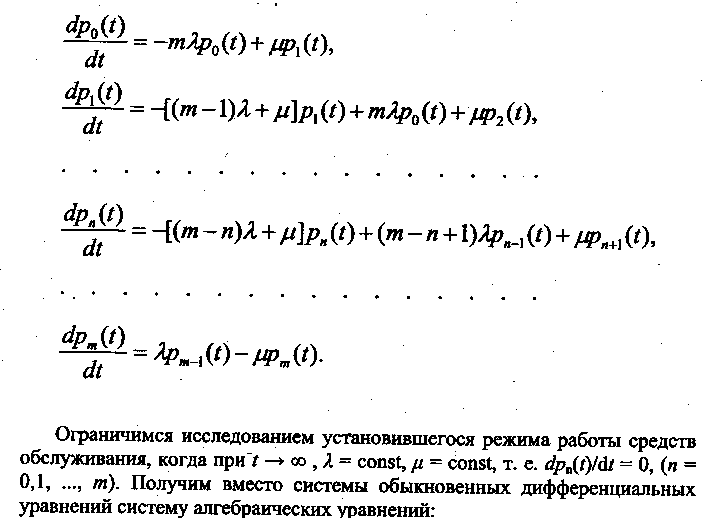
После определения всех этих количественных связей можно переходить к построению математической модели, т.е. развернутого выражения крите­рия оптимизации.

Построение математическое модели. Критерий оптимизации - удель­ные приведенные затраты с учетом эффекта, получаемого от досрочного ввода объекта в строй, запишется в таком виде:

Исследование математической модели. Запишем критерий оптимизации - математическую модель в несколько ином виде. Обозначим первое и по­следнее слагаемые через у,, не зависящие от числа обслуживаемых машин. Тогда математическая модель будет выглядеть так:

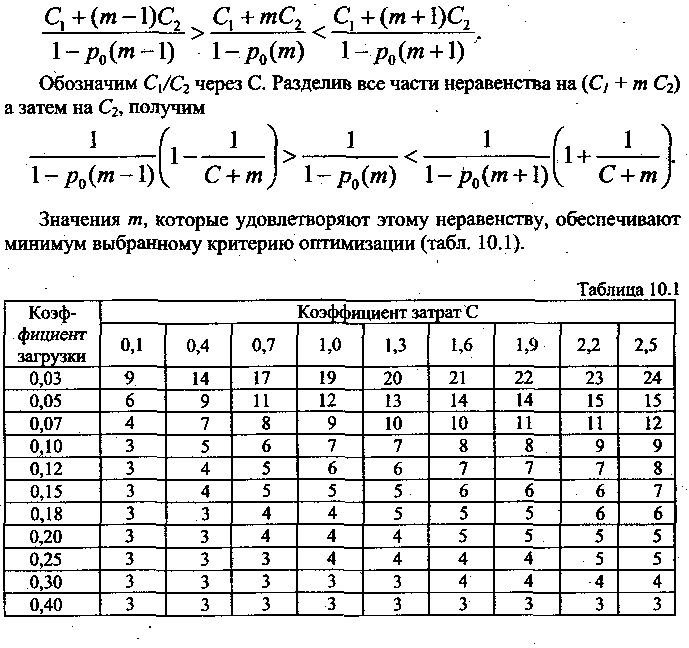
Как можно заметить, критерий оптимизации дискретно зависит от чис­ла обслуживаемых машин. Учитывая это, для определения искомого опти­мума оптимального числа обслуживаемых машин используем следующее неравенство:

или, проведя определенные сокращения, получим