5.2 Оптимальное комплектование машин экскаватор - автосамосвалы

При решении предыдущей задачи предполагалось, что экскаватор как ведущая машина задан, однако часто возникают ситуации в процессе меха­низации строительства, когда проектировщик или эксплуатационник имеют возможность использовать набор экскаваторов и автосамосвалов для строительства конкретного объекта. Перебор всех возможных комбинаций, сочетаний — задача довольно трудная, поэтому возникает необходимость опре­деления оптимального комплекта машин одноковшовый экскаватор — ав­тосамосвалы.

Постановка задачи и выбор критерия оптимизации. При заданных условиях работы известны: дальность транспортировки грунта, скорость транспортировки, плотность грунта, категория разрабатываемого грунта и ряд других факторов. Известны технико-экономические показатели работы различных типоразмеров экскаваторов и автосамосвалов. Требуется опре­делить такое сочетание параметров комплекта - вместимость ковша экска­ватора q и грузоподъемность автосамосвала g, при которых обеспечивается максимальная эффективность работы комплекта.

Выявление основных особенностей, взаимосвязей и количествен­ных закономерностей. В качестве критерия оптимизации, как и в преды­дущей задаче, используем удельные приведенные затраты, которые можно представить так:

Построение математической модели. Для определения оптимальных параметров комплекта машин экскаватор - автосамосвалы необходимо все вышеприведенные аналитические выражения и уравнения регрессии под­ставить в аналитическое выражение критерия оптимизации — удельные приведенные затраты. Получим математическую модель для определения оптимальных параметров комплекта машин экскаватор автосамосвалы.

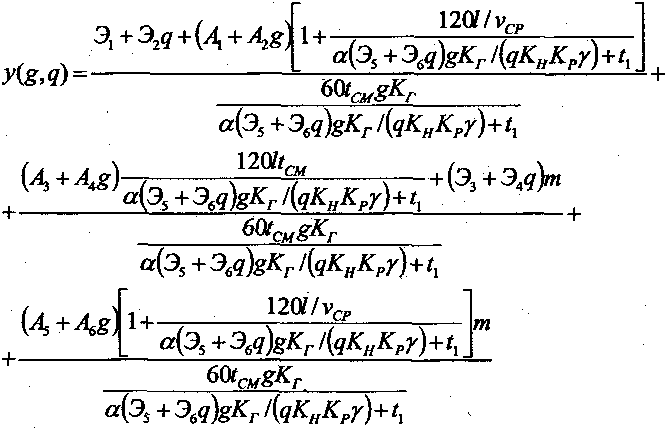
Исследование и решение математической модели.

Для отыскания искомых оптимальных параметров q и g, минимизи­рующих выбранный критерий оптимизации • у, необходимо определить соответствующие частные производные и приравнять их к нулю. Для уп­рощения выкладок будем полагать t1 = 0.

Частная производная по искомому параметру g - грузоподъемности ав­тосамосвала, приравненная к нулю, в начальном виде будет выглядеть так

Решив совместно систему уравнения dy/dg = 0 и dy/dq = O, най­дем оптимальные параметры комплекта одноковшовый экскаватор — авто­самосвалы. Для практических расчетов необходимо систему уравнений за­писать в таком виде:

Для определения оптимальных параметров можно использовать гра­фическое решение системы в координатах qOg.

После определения оптимальных параметров комплекта можно найти число автосамосвалов, необходимых для обслуживания одноковшового экскаватора,

Применение графоаналитического метода определения оптимальных параметров комплекта дает возможность быстро вычислить оптимальные параметры при сравнительно небольших затратах времени для различных условий эксплуатации из условия минимума приведенных затрат на разра­ботку и транспортировку единицы грунта.

Требуется определить оптимальные параметры комплекта одноковшо­вый экскаватор — автосамосвалы и потребное число автосамосвалов.

Решение. Оптимальные параметры комплекта будем искать, используя ранее полученную систему уравнений для определения g_onT и qопт.

Для облегчения поиска искомых оптимальных параметров предвари­тельно несколько упростим исходную систему уравнений. После подстановки всех начальных данных в систему уравнений для определения опти­мальных параметров — грузоподъемности автосамосвала и вместимости ковша экскаватора, получим следующую систему уравнений

Определение оптимальных параметров комплекта машин одноковшо­вый экскаватор — автосамосвалы выполним двумя методами: методом графического решения системы уравнений в координатах qOg и методом итераций.

1-й метод — графическое решение системы уравнений. Для этого по­строим графики g=f(q), используя первое уравнение системы q = ф (g) второе уравнение системы. Точка пересечения построенных графиков и определит оптимальные параметры.

2-й метод — метод итерации. Этот метод основан на последовательном приближении к искомому решению с помощью итеративного решения ис­ходной системы уравнений, используя такую запись системы уравнений.

Процесс итерации приостанавливают тогда, когда последующие значе­ния искомых параметров мало отличаются от предыдущих.

В нашем примере окончательно можно принять значения

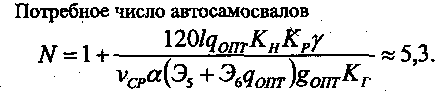
При графическом способе решения системы уравнений, построенные графики позволяют сделать много полезных выводов. Так, используя гра­фик g = f(q), можно легко найти оптимальную грузоподъемность goпт авто­самосвала при заданной вместимости ковша и при различных условиях экс­плуатации, например, дальности транспортирования грунта. Так для экска­ватора с вместимостью ковша q = 1,25 м³ при дальности транспортирования грунта L = 2 км необходимы автосамосвалы грузоподъемностью 19 т. При дальности транспортирования грунта I = 3 км - автосамосвалы грузоподъ­емностью 23 т.

Как можно заметить, для определения основных параметров функцио­нирования комплекта машин экскаватор автосамосвалы требуется произ­вести большой объем вычислений. Для эффективного выполнения необхо­димых расчетов целесообразно иметь соответствующее программное обес­печение. Ниже представлена соответствующая ФОРТРАН программа (прогр. 5.2).