4.4. Оптимизация структуры одноканального комплекта машин

Постановка задачи. Допустим, что исследуется функционирование не­которого комплекта машин (средств механизации), например, кран - пане­левозы, экскаватор — автосамосвалы, мастерская по ремонту машин - об­служиваемые машины и т.д. Известны основные технико-экономические показатели функционирования каждой машины комплекта, интенсивность поступления машины (машин) на обслуживание Л, интенсивность обслужи­вания каналом р.. Требуется определить оптимальную структуру комплекта, т.е. какое число машин должна обслуживать ведущая машина (канал об­служивания), чтобы удельные приведенные затраты с учетом прибыли, по­лучаемой от досрочного ввода объекта в строй, были минимальны.

Выявление основных особенностей взаимосвязей и количествен­ных закономерностей. Используя логико-аналитический анализ, сформи­руем критерий оптимизации (удельные приведенные затраты с учетом при­были от досрочного ввода объекта в строй), который может быть записан в таком виде:

Если работа комплекта машин не влияет на фактический срок строи­тельства объекта, например, имеется большой резерв времени, то возможно использование а качестве критерия оптимизации только удельных приве­денных затрат без учета прибыли, получаемой от досрочного ввода объекта

в строй.

Оговорим некоторые особенности функционирования рассматриваемой системы (комплекта машин). Допустим, что:

- вероятность поступления одной машины на обслуживание не зависит от вероятности поступления другой, т.е. мы имеем систему без последействия;

- вероятность поступления на обслуживание сразу двух и более машин равна нулю или столь мала, что ею можно пренебречь, т.е. мы имеем сис­тему машин с ординарным потоком машин в системе;

- вероятность поступления машины на обслуживание зависит только от интервала, но не зависит от расположения этого интервала на оси времени, т.е. мы имеем комплект машин со стационарным потоком поступления ма­шин на обслуживание.

Таким образом, мы имеем простейший поток, который обладает одно­временно свойствами стационарности, ординарности и отсутствием после­действия.

Следовательно, вероятность простоя ведущей машины определяется по

формуле:

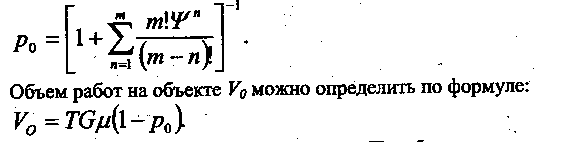
Построение математическое модели. Преобразуем, исходное выраже­ние критерия оптимизации так, чтобы можно было выделить в нем части, независящие и зависящие от числа обслуживаемых машин – m.

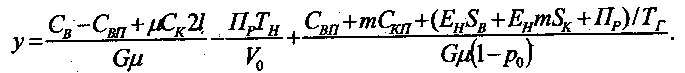
В результате такого преобразования в критерии оптимизации выделены три части, из которых первый и второй члены не зависят от числа обслуживае­мых машин т, а третий член - зависит. Обозначим первый и второй члены через у1 и несколько преобразуем третий член, тогда получим математиче­скую модель в таком виде:

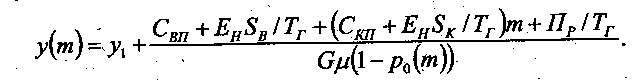
Исследование математической модели. Анализируя полученную ма­тематическую модель, можно заметить, что искомый параметр m – число машин, которые может эффективно обслуживать ведущая машина, прини­мает только целочисленное значение, следовательно, классические методы оптимизации в этой ситуации неприменимы. Для поиска оптимума вос­пользуемся следующим очевидным неравенством:

Если число обслуживаемых машин в комплекте мало, то будут значи­тельные простои ведущей машины, если же наоборот, то будет велик про-1 стой обслуживаемых машин. И в том, и в другом случае комплект будет 1 неэффективен.

Подставим в исходное неравенство математические выражения Критерия оптимизации с соответствующим числом обслуживаемых машин: (m-1), m, (m+1). При этом часть критерия оптимизации – у1 которая не зависит от числа обслуживаемых машин m, может быть опущена:

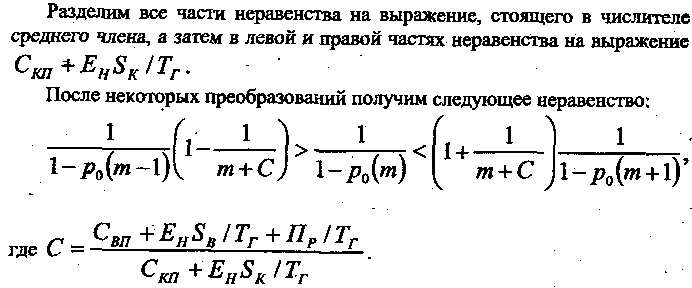
Назовем величину С коэффициентом затрат.

Для того, чтобы определить оптимальное число комплектующих машин в комплекте необходимо протабулировать полученное неравенство для различных значений т. Те из значений, которые будут удовлетворять неравенству, и будут искомыми оптимальными значениями.

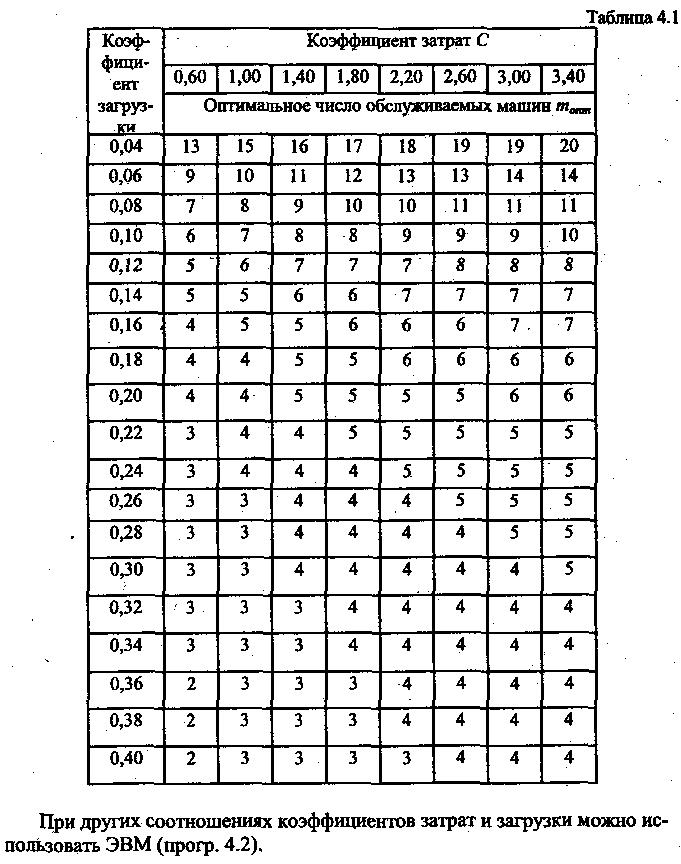
Для облегчения поиска оптимальной структуры одноканальной замкну­той системы (комплекта машин), для различных коэффициентов затрат С и коэффициентов загрузки проведены расчеты и результаты расчетов пред­ставлены в табл. 4.1.