Проверка статистических гипотез

Статистические гипотезы

Определения

Пусть в (статистическом) эксперименте доступна наблюдению случайная величина, распределение которой известно полностью или частично. Тогда любое утверждение, касающееся называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них:

• Статистическая гипотеза, однозначно определяющая распределение , то есть 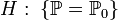, где какой-то конкретный закон, называется простой.

• Статистическая гипотеза, утверждающая принадлежность распределения к некоторому семейству распределений, то есть вида 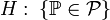, где 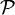 — семейство распределений, называется сложной.

На практике обычно требуется проверить какую-то конкретную и как правило простую гипотезу . Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза , называемая конкурирующей или альтернативной.

Выдвинутая гипотеза нуждается в проверке, которая осуществляется статистическими методами, поэтому гипотезу называют статистической. Для проверки гипотезы используют критерии, позволяющие принять или опровергнуть гипотезу.

В большинстве случаев статистические критерии основаны на случайной выборке фиксированного объема из распределения . В последовательном анализе выборка формируется в ходе самого эксперимента и потому её объем является случайной величиной.

Пример

Пусть дана независимая выборка из нормального распределения, где  — неизвестный параметр. Тогда , где  — фиксированная константа, является простой гипотезой, а конкурирующая с ней  — сложной.

Этапы проверки статистических гипотез

1. Формулировка основной гипотезы и конкурирующей гипотезы .

2. Задание уровня значимости 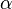, на котором в дальнейшем и будет сделан вывод о справедливости гипотезы. Он равен вероятности допустить ошибку первого рода.

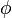3. Расчёт статистики критерия такой, что:

• её величина зависит от исходной выборки ;

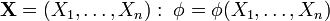• по её значению можно делать выводы об истинности гипотезы ;

• сама статистика должна подчиняться какому-то известному закону распределения, так как сама является случайной в силу случайности .

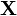4. Построение критической области. Из области значений выделяется подмножество 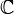таких значений, по которым можно судить о существенных расхождениях с предположением. Его размер выбирается таким образом, чтобы выполнялось равенство 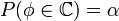. Это множество и называется критической областью.

5. Вывод об истинности гипотезы. Наблюдаемые значения выборки подставляются в статистику и по попаданию (или непопаданию) в критическую область выносится решение об отвержении (или принятии) выдвинутой гипотезы .

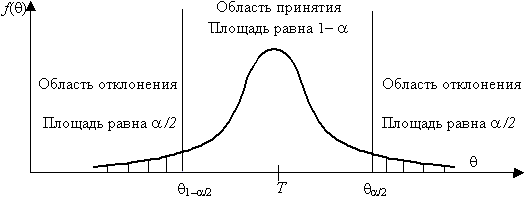
Виды критической области

Выделяют три вида критических областей:

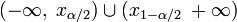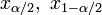• Двусторонняя критическая область определяется двумя интервалами , где находят из условий .

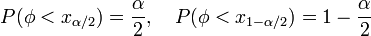• Левосторонняя критическая область определяется интервалом 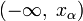, где 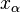находят из условия .

• Правосторонняя критическая область определяется интервалом 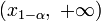, где 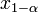находят из условия .

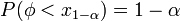Проверка гипотез 

1. Постановка задачи

Статистической гипотезой называется непротиворечивое утверждение, касающееся вида распределения имеющейся выборки.

Основная гипотеза, нуждающаяся в проверке называется нулевой или нуль-гипотезой. Любая другая гипотеза, относительно которой проверяют нуль-гипотезу, называется альтернативой. Например: пусть имеется выборка из распределения хи-квадрат с N степенями свободы. Нуль-гипотеза состоит в том, что –

H₀: N=2 ,

альтернатива –

H₁: N>2 .

На практике альтернативу часто опускают, формулируя только нуль-гипотезу.

Гипотеза называется простой, если она однозначно определяет функцию распределения выборки. В противном случае гипотеза называется сложной. В примере: H₀ – это простая гипотеза, а H₁ – это сложная альтернатива.

Гипотезы бывают параметрическими, когда вид распределения известен заранее, с точностью до численных значений его параметров – как в примере выше. Кроме того, гипотезы могут быть непараметрическими.

Например: пусть имеется выборка из неизвестного распределения F. Нуль-гипотеза состоит в том, что  –

H₀: F – это равномерное распределение.

2. Проверка гипотез

Метод проверки статистической гипотезы называется статистическим критерием. Он строится на основе имеющейся выборки x=(x₁,…, x_I) с помощью измеримой функции S(x), называемой статистикой критерия. В пространстве значений статистики S(x) выбирается область C, называемая критической. Если S(x) ∈ С, то гипотезу отклоняют (отвергают), в противном случае – принимают.

Статистика S(x) должна быть устроена особым образом – так, чтобы ее распределение не зависело от неизвестных  параметров распределения выборки x. Кроме того функция распределения S(x) должна быть табулирована заранее.

В большинстве практических приложений статистика S(x) строится из соображений нормальности.

3. Ошибки 1-го и 2-го родов

Проверка статистической гипотезы не дает ее логического подтверждения или опровержения. Проверка только утверждает, что "имеющиеся данные (не) противоречат» выдвинутому предположению". Поэтому при проверке статистической гипотезы возможны случайные ошибки, которые могут быть двух родов.

Ошибка 1-го рода происходит тогда, когда нуль-гипотеза верна, но отвергается согласно критерию.

Ошибка 2-го рода происходит тогда, когда нуль-гипотеза не верна, но принимается согласно критерию.

Вероятность ошибки первого рода называется уровнем значимости и обозначается α.

Обычно уровень значимости выбирается равным 0.01, 0.05, или 0.1 и по этому значению подбирают критическую область C_α.

4. Пример проверки гипотезы

Пусть имеется выборка x=(x₁,…, x_I) из нормального распределения  –

x_i ~ N(m, σ²)

с известной дисперсией σ² и неизвестным средним m.

Проверяется простая нуль-гипотеза  –

H₀: m=0.

Альтернативу мы сформулируем позже.

В качестве статистического критерия возьмем функцию

,

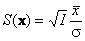которая при m=0 подчиняется стандартному нормальному распределению  –

S ~ N(0, 1) .

При заданном уровне значимости α критическая область определяется условием  –

Pr{|S|> C_α }= α .

Поэтому

C_α = Φ^–1(1– α/2).

Введем теперь альтернативную гипотезу  –

H₁: m=a ,

и найдем величину ошибки 2-го рода. Ее величина

β=Pr{|S|< C_α | m=a}

рассчитывается при условии

S  ~ N(а, 1).

Поэтому,

β=Φ(C_α –a) – Φ(–C_α –a) .

На листе Hypothesis приведены расчеты этого примера.  

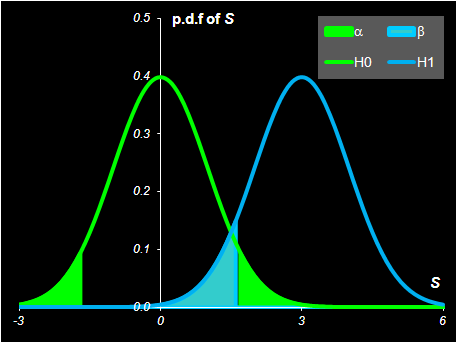
Рис.17 Ошибки 1-го и 2-го родов при проверке гипотез

5. Критерий согласия хи-квадрат

Критерий согласия хи-квадрат проверяет соответствие между теоретическими вероятностями P₁, P₂, …и их эмпирическими частотными оценками I₁/I, I₂/I,…

Для примера рассмотрим выборку x=(x₁,…, x_I) из неизвестного распределения  –

x_i ~ F(x).

Нуль гипотеза состоит в конкретизации этого распределения, т.е. в утверждении типа «F – это нормальное распределение с нулевым средним и дисперсией равной 2»

В соответствие с выбранным гипотетическим распределением, область изменения случайной величины X, разбивается на R классов (корзин) и рассчитываются теоретические вероятности P₁, P₂, …, P_R попадания в каждую из корзин. С другой стороны определяется, сколько элементов выборки попало в каждую из этих корзин – I₁, I₂, …, I_R и вычисляются эмпирические вероятности F_r=I_r/I.

Статистикой критерия согласия служит случайная величина

    ,

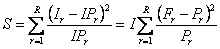(17)

которая при I → ∞ стремится к распределению хи-квадрат с R–1 степенями свободы. Число и размеры корзин надо выбирать так, чтобы

IP_r > 6 .

Критическая область на уровне значимости α определяется условием  –

S > χ^–2(1–α | R–1) .

Критерий согласия хи-квадрат можно применять и в том случае, когда теоретическое распределение F(x | p) известно с точностью до неизвестных параметров p =(p₁,…, p_M). Эти параметры предварительно оцениваются по той же выборке x и подставляются в функцию F(x | p). В этом случае следует изменить число степеней свободы на R–M–1.

6. F-критерий

Этот критерий применяется для проверки нуль-гипотезы о равенстве дисперсий в двух нормальных выборках: x=(x₁,…, x_I) и y=(y₁,…, yJ). Пусть   

 – суть оценки выборочных дисперсий, найденные по формуле.

Если

,

то обозначим

.

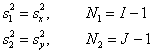Иначе  – 

.

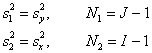Статистикой F-критерия служит случайная величина

,

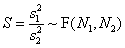которая подчиняется распределению Фишера с N1, N2 степенями свободы.

Критическая область на уровне значимости α определяется условием  –

S > F^–1(1–α | N₁, N₂) .

F-критерий очень чувствителен к нарушению предположения о нормальности распределений выборок, поэтому его не рекомендуется применять в практических приложениях.

3. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ

3.1. Сущность задачи проверки статистических гипотез

Статистическая гипотеза представляет собой некоторое предположение о законе распределения случайной величины или о параметрах этого закона, формулируемое на основе выборки [3, 5, 11]. Примерами статистических гипотез являются предположения: генеральная совокупность распределена по экспоненциальному закону; математические ожидания двух экспоненциально распределенных выборок равны друг другу. В первой из них высказано предположение о виде закона распределения, а во второй – о параметрах двух распределений. Гипотезы, в основе которых нет никаких допущений о конкретном виде закона распределения, называют непараметрическими, в противном случае – параметрическими.

Гипотезу, утверждающую, что различие между сравниваемыми характеристиками отсутствует, а наблюдаемые отклонения объясняются лишь случайными колебаниями в выборках, на основании которых производится сравнение, называют нулевой (основной) гипотезой и обозначают Н0. Наряду с основной гипотезой рассматривают и альтернативную (конкурирующую, противоречащую) ей гипотезу Н1. И если нулевая гипотеза будет отвергнута, то будет иметь место альтернативная гипотеза.

Различают простые и сложные гипотезы. Гипотезу называют простой, если она однозначно характеризует параметр распределения случайной величины. Например, если l является параметром экспоненциального распределения, то гипотеза Н0 о равенстве l =10 – простая гипотеза. Сложной называют гипотезу, которая состоит из конечного или бесконечного множества простых гипотез. Сложная гипотеза Н0 о неравенстве l >10 состоит из бесконечного множества простых гипотез Н0 о равенстве l =bi , где bi – любое число, большее 10. Гипотеза Н0 о том, что математическое ожидание нормального распределения равно двум при неизвестной дисперсии, тоже является сложной. Сложной гипотезой будет предположение о распределении случайной величины Х по нормальному закону, если не фиксируются конкретные значения математического ожидания и дисперсии.

Проверка гипотезы основывается на вычислении некоторой случайной величины – критерия, точное или приближенное распределение которого известно. Обозначим эту величину через z, ее значение является функцией от элементов выборки z=z(x1, x2, …, xn). Процедура проверки гипотезы предписывает каждому значению критерия одно из двух решений – принять или отвергнуть гипотезу. Тем самым все выборочное пространство и соответственно множество значений критерия делятся на два непересекающихся подмножества S0 и S1. Если значение критерия z попадает в область S0, то гипотеза принимается, а если в область S1, – гипотеза отклоняется. Множество S0 называется областью принятия гипотезы или областью допустимых значений, а множество S1 – областью отклонения гипотезы или критической областью. Выбор одной области однозначно определяет и другую область.

Принятие или отклонение гипотезы Н0 по случайной выборке соответствует истине с некоторой вероятностью и, соответственно, возможны два рода ошибок. Ошибка первого рода возникает с вероятностью a тогда, когда отвергается верная гипотеза Н0 и принимается конкурирующая гипотеза Н1. Ошибка второго рода возникает с вероятностью b в том случае, когда принимается неверная гипотеза Н0, в то время как справедлива конкурирующая гипотеза Н1. Доверительная вероятность – это вероятность не совершить ошибку первого рода и принять верную гипотезу Н0. Вероятность отвергнуть ложную гипот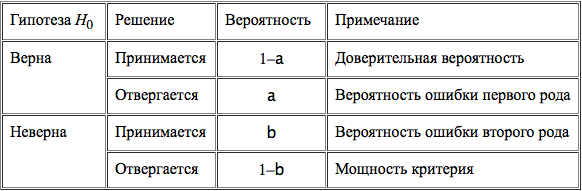 езу Н0 называется мощностью критерия. Следовательно, при проверке гипотезы возможны четыре варианта исходов.

Например, рассмотрим случай, когда некоторая несмещенная оценка параметра q вычислена по выборке объема n, и эта оценка имеет плотность распределения f(q ).