3. Деление должно быть непрерывным.

При делении необходимо переходить к ближайшему низшему роду. В случае несоблюдения этого правила возникает ошибка, называемая скачком в делении. Например, «гpaмматические предложения бывают простыми, сложноподчиненными и сложносочиненными». В этом делении имеется скачок. Если мы разделим грамматические предложения сначала на простые и сложные, а затем сложные предложения разделим на сложносочиненные и сложноподчиненные, скачка в делении не произойдет.

Виды деления

1. При делении по видоизменению признака основанием деления будет служить признак, при изменении которого образуются видовые понятия, входящие в о6ьем делимого (родового) понятия. Например: «государства по форме правления делятся на монархические и республиканские, по форме государственного устройства - на унитарные и федеративные».

2. При дихотомическом делении (деление надвое) объем .делимого понятия А делится на два исчерпывающих его взаимоисключающих множества В и не-В. Например: «современные государства можно разделить на республиканские и нереспубликанские».

3. Классификацией называется распределение предметов по классам согласно сходству и различию между ними, которое производится с таким расчетом, чтобы каждый класс занимал фиксированное место в системе других классов. Классификация отличается от деления тем, что она представляет собой многоступенчатое деление. Классификация может быть вспомогательной или естественной. Вспомогательная классификация создается с целью наиболее легкого отыскания того или иного предмета среди множества классифицируемых предметов. Примером служит распределение фамилий учащихся в списке классного журнала по буквам алфавита. Естественная классификация - это распределение по группам на основании их существенных признаков. Классическим примером естественной классификации служит периодическая система химических элементов Д.И.Менделеева.

СУЖДЕНИЕ

Понятие не может быть ни истинным, ни ложным, пока не войдет в состав суждения. Суждение делает какие-то утверждения о вещах, говорит о том, чем они являются или не являются: «Ель зеленая», «Некоторые рефлексы не являются условными». Поэтому в отличие от понятия суждение всегда можно оценить как истинное или ложное.

Суждение - это такая форма мышления, которую отличают свойства:

1) что-либо утверждать или отрицать

2) Выражать либо истину, либо ложь.

Любое предложение можно рассматривать как суждение, когда его можно оценить с точки зрения истинности. Таковыми не являются только побудительные и вопросительные предложения.

Наиболее распространенными и лучше всего изученными являются категорические суждения. В них указывается принадлежность предметам тех или иных свойств: «металлы электропроводны», «некоторые газеты являются ежедневными». Наряду с ними имеются также суждения отношений: «Киев древнее Москвы», «десять больше семи». Их отличительная особенность состоит в том, что отмечаемое ими свойство нельзя отнести к одному объекту. Еще одну группу образуют суждения существования, с помощью которых отмечается наличие в действительности тех или иных явлений: «существуют различные философские школы», «не существует 31 апреля».

СТРУКТУРА ПРОСТЫХ СУЖДЕНИЙ

В содержании суждения прежде всего имеются два важнейших компонента - субъект и предикат. Субъект (S) - это понятие, отображающее предмет, о котором идет речь. Предикат (Р) можно уподобить логическому сказуемому, поскольку этот структурный элемент выражает свойства, приписываемые предметам из объема понятия-субъекта или отрицаемые у них.

В суждении «роза красная» субъектом является «роза», а предикатом – «красная». В отличие от предложения все содержание суждения распределяется только между двумя составными частями - субъектом и предикатом.

Помимо субъекта и предиката в составе суждения имеются еще два структурных элемента, которые, однако, задают логические свойства суждений как форм мышления, а не их содержание. Один из них - связка. Она обозначается словами «есть», «является» и другими эквивалентными им выражениями.

Без связки суждения не бывает, потому что без нее нельзя было бы задать отношение между предметом и его свойством - принадлежит оно предмету или не принадлежит.

Последний структурный элемент суждения - квантор. Он выражается словами «все», «никакой», «некоторый» и другие. Он служит для указания количественной характеристики суждения - общее оно или частное.

Если понятие, стоящее на месте субъекта, берется во всем объеме, то суждение общее. «Все млекопитающие – позвоночные» - пример общего суждения.

В том случае, когда говорится о части объема субъекта, тогда перед нами частное суждение. Примером таковых могут быть: «некоторые товары ввозятся контрабандным путем», «большинство психических актов протекает бессознательно».

По количеству можно выделить еще одну категорию - единичные суждения, у которых в качестве субъекта берется единичное понятие: «данная заметка уже опубликована», «Кутузов не командовал русской армией в 1812 году до начала августа». По своим логическим свойствам единичные суждения относятся, однако, к суждениям общим. Для определения их количества решающее значение имеет то, что в суждении такого рода всегда охватывается весь объем понятия - субъекта. Частей у таких объемов просто не бывает.

КЛАССИФИКАЦИЯ СУЖДЕНИЙ

Все суждения делятся по качеству на две категории - утвердительные и отрицательные, и по количеству тоже на две - общие и частные. В логике принято объединять эти две пары категорических суждений в единую классификацию, в которой получается четыре вида.

а) всякое S есть Р - (А) - общеутвердительное суждение

б) ни одно S не есть Р - (Е) - отрицательное суждение

в) некоторые S суть Р - (I) - частноутвердительное суждение

г) некоторые S не суть Р - (О) - частноотрицательное суждение

где S - субъект суждения, Р - предикат суждения.

Общеутвердительное суждение.

Такие суждения являются общими по количеству и утвердительными по качеству - всем предметам приписывается какое-то свойство. Их принято обозначать буквой A (a) - первой гласной латинского affirmo (утверждаю).

Примеры:

1) «Все планеты - небесные тела».

2) «Квадрат - прямоугольник с равными сторонами».

3) «Уральские горы протянулись с севера на юг».

4) «Данное преступление совершено вчера».

Общеотрицательное суждение.

Такие суждения являются общими по количеству и отрицательными по качеству - у всех предметов отрицается какое-либо свойство. Их обозначают первой гласной из латинского nego (отрицаю) - E (e).

Примеры:

1) «Никакая параллель не пересекает экватор».

2) «Дельфин не рыба».

3) «Ни одна война не обходится без жертв».

Частноутвердительное суждение

Этот вид суждения образуется тогда, когда части предметов приписывается какое-то свойство. Символическим обозначением ему служит вторая гласная из того же слова affirmo – I (i).

Примеры:

1) «Некоторые студенты изучают китайский язык».

2) «Некоторые врачи – стоматологи».

3) «Преступники порой избегают наказания».

Частноотрицательное суждение

Такие суждения являются частными по количеству и отрицательными по качеству. Для их обозначения берется вторая гласная из слова nego - O (o).

Примеры:

1) «Некоторые законы не имеют обратной силы».

2) «Большинство музыкантов не скрипачи».

3) «Иные из бабочек не являются однодневками».

РАСПРЕДЕЛЕННОСТЬ ТЕРМИНОВ В СУЖДЕНИЯХ

Свойства суждений определяются еще одним важным показателем - распределенностью их терминов. Термины суждения – это S и P. Термины можно рассматривать со стороны их объема. Термин суждения является распределенным, если он взят в нем во всем объеме, то есть из суждения видно, что все предметы его объема обладают (не обладают) каким-то свойством. Термин суждения является нераспределенным, если он берется не во всем объеме - лишь часть предметов его объема обладает (не обладает) каким-то свойством.

Распределенность обозначается знаком «+», нераспределенность знаком «-». Например: «Все студенты нашей группы – спортсмены». S - «студенты нашей группы» распределён, т.к. в суждении говорится обо всех студентах нашей группы. Р - «спортсмены» - не распределен, т.к. кроме спортсменов нашей группы есть много других спортсменов, в другой группе, в стране вообще.

Для распределенности имеет значение только полнота знаний об объеме. Характеризуется ли термин в утвердительной форме (ему приписывается свойство) или в отрицательной (отрицается таковое у него), не играет роли.

В общеутвердительном суждении (А) субъект всегда распределен (S+).

На это указывает квантор. Предикат же, как правило, не распределен. Если понятие S содержится в объёме поня­тия Р, то символически мы можем это представить при помощи круга S, который находится внутри круга Р.

Пример: «Все караси – рыбы» (все караси – рыбы, но не все рыбы – караси).

S подчинён P: S+ P- .Субъект распределен, так как мыслится в полном объеме, предикат не распределен, поскольку его объем не исчерпывается лишь объемом субъекта.

Но могут быть и исключения, когда субъект (S) и предикат (P) образуют равнозначные понятия и тогда оба термина - и S, и P - распределены.

Например, «Все люди суть разумные существа» и «Александр Сергеевич Пушкин – автор романа “Евгений Онегин». S и P равнозначны: S+ P+

В общеотрицательном суждении (Е) оба термина всегда распределены (S+ P+).

Раз в нем прямо отрицается принадлежность всех предметов одного класса к предметам другого, то тем самым отрицается и принадлежность всех предметов второго к первому. Значит, в общеотрицательных суждениях оба термина характеризуются в полном объеме как не принадлежащие к какому-то классу предметов.

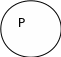
Например, «Ни один крокодил не летает». Объём S и объём P полностью исключают друг друга: S+ P+. И субъект, и предикат являются распределенными.

Частноутвердительное суждение (I) всегда имеет нераспределенный субъект (S-), на это указывает квантор «некоторые». Предикат чаще всего не является распределенным.

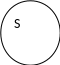
Например, «Некоторые юристы являются депутатами Государственной Думы». S и P перекрещивающиеся понятия, S- P-, так как они мыслятся не в полном объеме. Но здесь тоже бывают исключения. Они относятся к тем случаям, когда между S и P отношения подчинения, S подчиняет себе P.

Например, в суждении «Некоторые музыканты - скрипачи» понятие скрипачей полностью входит в понятие музыкантов. P подчиняется S: S- P+. Следовательно, термин, стоящий на месте предиката в таком суждении оказывается распределенным.

В частноотрицательном суждении (О) субъект не распределен (S-), так как мыслится лишь в некоторой части, а предикат распределен (P+)., поскольку его объем полностью исключен из объема субъекта. Часть объёма S несовместима с объёмом P. Например, «Некоторые студенты не являются спортсменами».

В других случаях, когда между S и P отношения подчинения, S подчиняет себе P, схема меняется. Например, суждение «Некоторые змеи не имеют ядо­витых зубов».

Из объёма S только часть S, которая находится в круге Р, обозначает тех змей, которые имеют ядовитые зубы. Та часть, которая находится вне круга Р, будет обозна­чать змей, которые не имеют ядовитых зубов. Следовательно, субъект является нераспределенным, предикат - распределенным.

Таким образом, субъект всегда распределен в общих суждениях и не распределен в частных. Предикат всегда распределен в отрицательных суждениях и распределен в утвердительных тогда, когда по объему P ≤ S.

Без знания правил распределенности терминов в суждениях отпадает один из способов проверки правильности построения категорических силлогизмов или непосредственных умозаключений.

ОТНОШЕНИЯ МЕЖДУ СУЖДЕНИЯМИ

ЛОГИЧЕСКИЙ КВАДРАТ

Между суждениями существуют определенные логические отношения. Сравнимые сужения, имеющие одинаковые термины (субъект и предикат) сопоставимы по истинности и ложности. Логические отношения между ними иллюстрируются с помощью логического квадрата. Буквы на углах квадрата символизируют различные виды суждений - A, E, I, O. А его стороны и диагонали выражают всю совокупность возможных отношений между ними.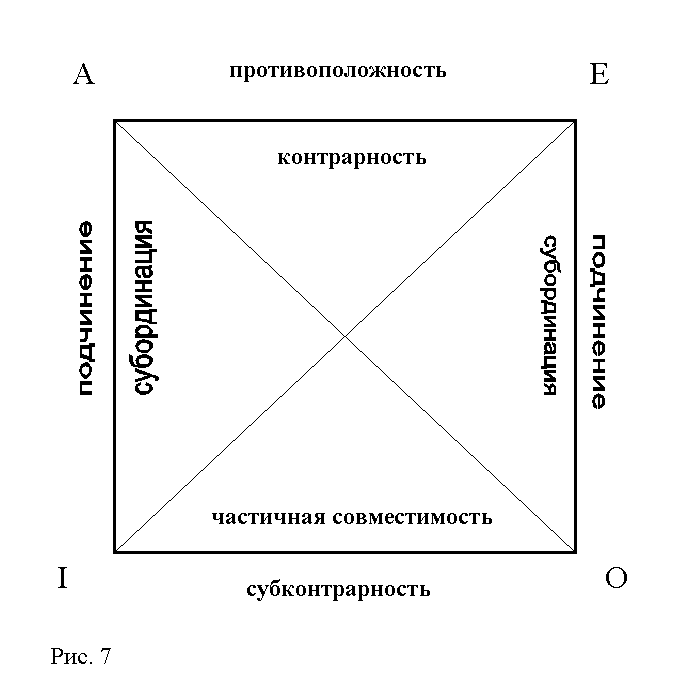

Отношения противоречия (контрадикторности): А - О, Е – I.

Эти суждения не бывают ни одновременно истинными, ни одновременно ложными. Из истинности одного суждения следует ложность другого, из ложности одного – истинность другого. Выводы строятся по схемам: Аи - Ол, Ал – Ои, Еи – Iл, Ел – Iи.

Отношения противоположности (контрарности): А - Е.

Противоположные суждения не могут быть одновременно истинными, но могут быть одновременно ложными. Из ложности одного суждения следует истинность другого, но из истинности одного из них может следовать как истинность, так и ложность другого суждения. Bывoды строятся по схемам: Аи - Ел, Еи - Ал; Ал – Е?, Ел – А?.

Отношения частичной совместимости (субконтрарности): I - О.

Эти суждения могут быть одновременно истинными, но не могут быть одновременно ложными. Из ложности одного суждения следует истинность другого, но из истинности одного из них может следовать как истинность, так и ложность другого. Выводы строятся по схемам: Iл - Ои, Ол - Iи, Iи – О?, Ои – I?

Отношения подчинения: А – I, Е – О.

Из истинности подчиняющего суждения следует истинность подчиненного суждения, но не наоборот: из истинности подчиненного суждения истинность подчиняющего суждения не следует, оно может быть истинным, но может быть и ложным. Из ложности подчиненного суждения следует ложность подчиняющего суждения, но не наоборот.

Законы логического квадрата, как и остальные логические законы, не зависят от содержания высказываний. О чем бы ни шла речь, все отмеченные правила действуют неукоснительно. Даже если нам непонятно содержание, то все равно, опираясь на одну только логическую форму, можно сделать правильные выводы или проверить, верно ли построено то или иное рассуждение с использованием одинаковых терминов суждений.

СЛОЖНЫЕ СУЖДЕНИЯ

Суждения, состоящие более чем из одногo простогo суждения, называются сложными.

Сложные суждения, образованные посредством связи двух или нeскольких прocтых суждений логическим союзом «и», называются соединительными (конъюнктивными). Логический союз «и» и равнозначные ему слова и союзы обозначаются знаком « ». Например, «на улице холодно и идет дождь».

Зависимость истинности конъюнктивного суждения от истинности исходных суждений можно изобразить в виде следующей таблицы:

А	В	А  В
1	1	1
1	0	0
0	1	0
0	0	0

где 1 - значение «истинно»,

0 - значение «ложно».

Сложные суждения, образованные посредством связи двух или нeскольких простых суждений логическим союзом «или», называются разделительными или (дизъюнктивными). Например, «истец вправе увеличить или уменьшить размер исковых требований». Дизъюнктивная связь выражается также словами «либо», «а также», «равно» и т.п.

Простая дизъюнкция: возможные мыслимые признаки предметов не исключают друг друга. Строгая дизъюнкция: возможные мыслимые признаки предметов исключают друг друга. Дизъюнкция обозначается знаком «».

Таблица истинности для дизъюнкции:

Простая дизъюнкция:

А	В	А  В
1	1	1
1	0	1
0	1	1
0	0	0

Строгая дизъюнкция:

А	В	А  В
1	1	0
1	0	1
0	1	1
0	0	0

Сложные суждения, образованные посредством связи нeскольких простых суждений с помощью союза «если… то», называются условными или импликативными. Импликация обозначается знаком «». Например: «если на улице идет дождь, то асфальт мокрый».

Таблица истинности для импликации:

А	В	А  В
1	1	1
1	0	0
0	1	1
0	0	1

Сложные суждения, связанные между собой с помощью союзов «если только, если», «тогда и только тогда» и т.п., называются суждениями тождества или эквивалентности. Обозначается данный логический союз с помощью знака «»

Таблица истинности для суждений тождества или эквивалентности:

А	В	А  В
1	1	1
1	0	0
0	1	0
0	0	1

Достаточные и необходимые условия

В научном познании важно проводить различие между достаточными и необходимыми условиями наступления какого-то факта, события, отражаемого в условном суждении. Условия являются достаточными, если при их выполнении всегда наступает данное событие. Условия являются необходимыми, если без их выполнения данное событие никогда не наступает. Так, в импликативном суждении АВ А является достаточным условием для В, а В - необходимым условием для А.

УМОЗАКЛЮЧЕНИЯ

НЕПОСРЕДСТВЕННЫЕ УМОЗАКЛЮЧЕНИЯ

Умозаключение - это форма мышления, посредством которой из одного или нескольких суждений с необходимостью выводится суждение, заключающее в себе новое знание. Суждения, из которых делается вывод, называются посылками умозаключения. Суждение, являющееся выводом умозаключения, называется заключением.

Пример:

Все жидкости - упруги.

Ртуть - жидкость.

Следовательно, ртуть - упруга.

В этом умозаключении из двух посылок «Все жидкости упруги» и «Ртуть - жидкость» выводится заключение «Ртуть упруга», в котором содержится новое знание.

Вообще умозаключение яв­ляется результатом сопоставления ряда посылок. Но есть вид умозаключений, основывающихся на одной посылке. Например, имея суждение: «ни один металл не есть сложное тело», можно сделать вывод, что «ни одно сложное тело не есть металл». Умозаключение, в котором заключение выводится из одной посылки, называется непосредственным. Непосредственные умозаключения позволяют избегать неясностей и двусмысленностей, проясняют смысл высказываний. Уточнение наших знаний происходит в таких непосредственных умозаключениях, как превращение, обращение, противопоставление предикату.

НЕПОСРЕДСТВЕННЫЕ УМОЗАКЛЮЧЕНИЯ

Превращение

Превращением называется такое непосредственное умозаключение, в котором в выводе субъектом является субъект исходного суждения, а предикатом – понятие, противоречащее предикату исходного суждения; при этом связка заменяется на противоположную.

Смысл превращения заключается в изменении формы суждений: утвердительные суждения пре­вращаются в отрицательные, и наоборот; при этом смысл суждения не изменяется.

Чтобы превратить утвердительное суждение, нaдo внести в него два отрицания: одно – в предикат (превратив его в не-Р), второе - в связку перед словом «eсть». Чтобы превратить отрицательное суждение, нужно убрать имеющееся в его связке перед «есть» отрицание и внести отрицание в предикат (превратив его в не-Р).

Примеры превращения одних суждений в другие:

1. Суждение А «все металлы суть эле­менты» превращается в суждение Е: «ни один металл не есть не­элемент»

2. Суждение Е «ни один человек не бывает совершенен» превращается в суждение А: «все люди суть несо­вершенны».

3. Суждение I «некоторые люди надёжны» превращается в суждение О: «некоторые люди не есть не­надёжны».

4. Суждение О «некоторые люди не есть надёжны» превращается в суждение I: «некоторые люди суть ненадёжны».

Обращение

Обращением называется такое непосредственное умозаключение, в котором в выводе субъектом является предикат исходного суждения, а предикатом – субъект исходного суждения, при этом связка остается неизменной.

Например, суждение «все спортсмены - здоровые люди» обращается в суждение «некоторые здоровые люди - спортсмены».

Обращение без ограничения объема называется простым или чистым обращением. Например, «некоторые школьники - шахматисты» обращается в «некоторые шахматисты - школьники».

Чтобы обратить суждение (т.е. построить новое суждение, в котором предикат станет субъектом, а объект - предикатом), нужно выяснить качество и количество этого суждения, а затем уже применять правила обращения. Нужно при этом помнить следующее: суждения типа А, как правило, обращаются с ограничением, но в тех случаях, когда субъект и предикат являются равнозначными понятиями, имеет место чистое обращение, т.е. суждение типа А обращается в А.

Например, суждение «всякая молекула воды имеет формулу H2O» обращается в «всякая молекула, имеющая формулу H2O, есть молекула воды».

Суждение типа I, как правило, чисто обращаемое, может обращать с приращением (т.е. в суждение А), если субъект суждения является родовым понятием по отношению к предикату. Например, суждение «некоторые художники - пейзажисты» обращается в суждение «все пейзажисты - художники» (но не «некоторые»).

Частноотрицательные суждения (О) - не обращаются.

Таким образом, смысл операции обращения суждений заключается в том, что в выводе субъектом является не предмет, выраженный субъектом посылки, а предмет, выраженный предикатом посылки. Обращение играет большую роль в проверке правильности определений.

Противопоставление предикату

Противопоставлением предикату называется такое непосредственное умозаключение, в котором в выводе (в новом суждении) субъектом является понятие, противоречащее предикату исходного суждения, а предикатом - субъект исходного суждения; при этом связка меняется на противоположную.

При противопоставлении предикату нужно помнить, что:

1) суждение cначала нужно превратить, а потом обратить;

2) суждение частноутвердительное (I) нельзя противопоставить предикату.

Например:

Все млекопитающие - позвоночные животные.

Превращение

Ни одно млекопитающее не является беспозвоночным животным.

Обращение

Ни одно беспозвоночное животное не является млекопитающим.

Суть преобразования посредством противопоставления предикату состоит в том, что в новом суждении предметом нашей мысли является предмет, выраженный понятием, противоречащим предикату исходного суждения. В этом смысле полученный вывод дает новое значение.

ДЕДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ.

ПРОСТОЙ КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ

Дедуктивные умозаключения принимают форму силлогизма. Силлогизм есть такая форма умозаключения, в которой из двух суждений необходимо вытекает третье, причём одно из двух данных суждений является общеутвердительным или общеотрицательным. Силлогизм, таким образом, представляет собой умозаключение от общего. Полученное суждение ни в коем случае не будет более общим, чем суждения, из которых оно выводится. Пример:

Все студенты имеют зачетные книжки.

Иванов - студент.

Следовательно, Иванов имеет зачетную книжку.

Данные суждения называются посылками, а новое суждение называется заключением. Те понятия, которые входят в заключение и посылки, называются терминами. Субъект заключения называется меньшим термином, предикат заключения называется большим термином, а термин, который не входит в заключение, называется средним термином. Самый больший объём приходится на долю предиката заключения, самый меньший — на долю меньшего термина, субъекта заключения, а средний — на долю среднего термина. Это наглядно обнаруживается, если изобразить отношение между терминами схематически.

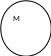
Средний термин называется средним также потому, что он служит связующим элементом между большим и меньшим терминами. Суждение, в которое входит больший термин, называется большей посылкой; суждение, в которое входит меньший термин, называется меньшей посылкой.

В силлогизме нужно отличать содержание от формы. Содержание — это термины, которые имеются налицо. Форма есть связь, которая придаётся нами терминам посылок. В силлогизме мы можем не обращать никакого внимания на истинность или ложность посылок. Для нас важно только сделать правильный вывод, совершить правильное умозаключение, правильно связать больший термин с меньшим, а это и есть форма силло-гизма. Поэтому иногда посылки могут быть ложными, а заключение будет всё-таки истинным, как это можно видеть из следующего силлогизма, посылки которого состоят из очевидно ложных суждений:

Львы суть травоядные.

Коровы суть львы.

Коровы суть травоядные.

Нахождение терминов и посылок

Чтобы найти термины и посылки в силлогизме, нужно:

1. Найти, которое из трех данных суждений является заключением (заключение обычно помещается после слов «значит», «следовательно» и т.п. или перед словами «потому что», «ибо», «так как»).

2. Найти субъект (это меньший термин) и предикат (это больший термин) заключения.

З. Найти посылку, в которой содержится больший термин; это и будет большая посылка.

4. Найти средний термин, т.е. понятие, которое содержится в каждой из посылок, но отсутствует в заключении.

Пример:

Лжедмитрий II не был воспитан иезуитами, ибо все, кто получил воспитание у иезуитов, знали хорошо латынь, а Лжедмитрий II не знал хорошо латыни.

1. Заключение находится перед словом «ибо»: «Лжедмитрий II не был воспитан иезуитами».

2. Су6ъект заключения - «Лжедмитрий II», это - меньший термин. Предикат заключения - «воспитан иезуитами», это - больший термин.

3. Большей посылкой будет суждение: «Все, кто получил воспитание у иезуитов, хорошо знали латынь», так как здесь содержится больший термин. Меньшая посылка - «Лжедмитрий не знал хорошо латыни», так как здесь содержится меньший термин («Лжедмитрий II»).

4. Понятие «знал (не знал) хорошо латыни» содержится в обеих посылках, но отсутствует в заключении; это понятие - средний термин.

Таким образом, простой категорический силлогизм - это умозаключение об отношении двух крайних терминов на основании знания их связи со средним термином.

Общие правила категорического силлогизма

Существует семь общих правил силлогизма: три правила терминов и четыре правила посылок.

Правила терминов

1. В каждом силлогизме должно быть только три термина.

Если даётся более трёх терминов, то силлогизм не получится. Например:

Все ораторы тщеславны.

Цицерон был государственным человеком.

В данных двух суждениях четыре термина, и вывода сделать нельзя. Если бы второе суждение было: «Цицерон - оратор», то можно было бы сделать вполне определённый вывод.

Иногда в силлогизме бывает четыре термина, а на первый взгляд кажется, что их только три. Это происходит вследствие двусмысленности терминов. Например:

Лук есть оружие дикарей.

Это растение есть лук.

Это растение есть оружие дикарей.

Ошибка происходит вследствие учетверения терминов, т.к. средний термин в большей посылке употреблен не в том же смысле, в каком употреблен в меньшей посылке.

2. Средний термин должен быть распределен по крайней мере в одной из посылок. Например:

Все французы суть европейцы.

Все парижане суть европейцы.

Из этих двух посылок нельзя сделать никакого заключения. Но если бы средний термин мы взяли хоть в одной посылке во всём объёме, то заключение можно было бы сделать. Напри­мер:

Все европейцы суть грамотны.

Все французы суть европейцы.

Следовательно, все французы суть грамотны.

3. Термин не может быть распределен в заключении, если он не распределен в посылке. Например:

Все преступники заслуживают наказания,

Некоторые англичане суть преступники.

Все англичане заслуживают наказания.

Очевидная ошибка в этом силлогизме получается вследствие того, что в заключении термин «англичане» распределен, между тем как в посылке этот термин взят не во всём объёме. Мы бы сделали правильное заключение, если бы сказали: «некоторые англичане заслуживают наказания».

Правила посылок

1. Из двух отрицательных посылок нельзя сделать вывода.

2. Из двух частных посылок нельзя сделать заключения.

3. Если одна из посылок отрицательная, то и заключение должно быть отрицательным.

4. Если одна из посылок частная, то и заключение должно быть частным.

Фигуры и модусы категорического силлогизма

Фигурами силлогизма называются формы силлогизма, различаемые по положению среднего термина (М) в посылках. Всего возможны 4 фигуры.

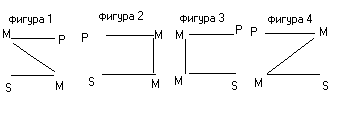
Примеры:

1. М Р

Все цветы - растения.

S M

Все розы - цветы.

S Р

Все розы - растения.

2. P М

Все рыбы дышат жабрами.

S M

Ни один кит не дышит жабрами

S Р

Ни один кит не является рыбой

3. М Р

Все углероды - простые тела.

М S

Все углероды - электропроводны.

S Р

Некоторые электропроводники - простые тела.

4. Р М

Все ужи - пресмыкающиеся.

М S

Ни одно пресмыкающееся не есть беспозвоночное.

S Р

Ни одно беспозвоночное не есть уж.

Особые правила фигур

1фигура. Большая посылка должна быть общим суждением.

Меньшая посылка - утвердительное суждение.

2 фигура. Большая посылка - общее суждение.

Одна из посылок - отрицательное суждение.

3 фигура. Меньшая посылка - утвердительное суждение.

Заключение - частное суждение.

4 фигура. Общеутвердительных заключений не дает.

Модусы категорического силлогизма.

Модусами категорического силлогизма называются разновидности силлогизма, отличающиеся друг от друга количественной и качественной характеристиками входящих в них посылок и заключения.

Всего правильных модусов в 4 фигурах 19.

1 фигура имеет правильные модусы:

ААА ЕАЕ АII EIO

2 фигура:

AEE AOO EAE EIO

3 фигура:

AAI EAO AII EIO IAI OAO

4 фигура:

AAI AEE IAI EIO EAO

СОКРАЩЕННЫЙ СИЛЛОГИЗМ (ЭНТИМЕМА)

Энтимема - в переводе с греческого языка означает «в уме», «в мыслях». Это название говорит о том, что та или иная часть силлогизма подразумевается, а не высказывается. В процессе мышления мы часто не высказываем всех частей силлогизма, а мыслим энтимемами.

Энтимемой называется силлогизм, в котором пропущена одна из посылок или заключение.

Чтобы восстановить энтимему в пoлный силлогизм, следует руководствоваться следующими правилами:

1. Найти заключение и так eго сформулировать, чтобы больший и меньший термины были четко выражены.

2. При нахождении посылок и заключения следует исходить из того, что заключение обычно помещается после слов «значит», «следовательно» и т.п. или перед словами «потому, что», «ибо», «так как».

3. Если опущена одна из посылок, а заключение наличествует, то нужно установить, какая из них (большая или меньшая) имеется. Это производится путем проверки, какой из крайних терминов содержится в данной посылке. Если больший термин, значит, имеется большая посылка, если в посылкe присутствует меньший термин, значит, меньшая посылка.

4. Зная, какая из поcылок опущена, а также зная средний термин, можно опредeлить оба термина недостающей посылки.

Например: «Собака не может лазать по портьерам, Ватсон, следовательно, это не собака» (Ш. Холмс).

Весь силлогизм можно записать в следующем виде:

Собака (P) не может лазать по портьерам (M).

Данное животное (S) может лазать по портьерам (M).

Данное животное (S) - не собака (P).

УСЛОВНЫЙ СИЛЛОГИЗМ

Силлогизм, в котором по крайней мере одна из посылок – условное суждение, называется условным. Силлогизм, в котором обе посылки являются условными, называется чисто условным или гипотетическим.

Например:

Если будет солнечный день (А), то вода в реке будет теплой (В).

Если вода в реке будет теплой (В), можно пойти купаться (С).

Если будет солнечный день, можно пойти купаться.

Чисто условный силлогизм выражается формулой:

А® В

(В® С)

А® С

Силлогизм, в котором одна из посылок – условное суждение, а другая – категорическое, называется условно-категорическим. Та часть условного суждения, которая начинается словом «если» и стоит перед знаком импликации (А), называется основанием. Та его часть, которая начинается словом «то» и находится после знака импликации (В), называется следствием.

Например:

Если взлетная полоса покрыта льдом (А), то самолеты не могут взлетать (В).

Сегодня взлетная полоса покрыта льдом (А).

Значит, сегодня самолеты не могут взлетать (В).

Условно-категорический силлогизм имеет два правильных модуса: утверждающий и отрицающий.

В утверждающем модусе (modus ponens) первая посылка представляет собой условное суждение, вторая посылка является утверждением основания, а в выводе утверждается следствие.

Если Луна в новолуние находится в узле своей орбиты (А), то происходит солнечное затмение (В).

Луна в новолуние находится в узле своей орбиты (А).

Следовательно, происходит солнечное затмение (В).

Его схема:

А® В, А

В

Вывод состоятелен, так как соответствует правильной схеме утверждающего модуса.

Утверждать можно только от основания к следствию, т.е. во второй посылке утверждающего модуса должно утверждаться основание первой посылки, а в выводе — ее следствие.

В отрицающем модусе (modus tollens) условно-категорического силлогизма первая посылка представляет собой условное суждение, вторая посылка является отрицанием следствия, а в выводе отрицается основание.

Например:

Если дождь идет (А), то трава мокрая (В).

Трава не мокрая (не-В).

Значит, дождя не было (не-А).

Этот силлогизм имеет схему:

А® В, не-В

не-А

Отрицать можно только от следствия к основанию, т.е. во второй посылке отрицающего модуса должно отрицаться следствие первой посылки, а в выводе - ее основание.

Возможны еще две разновидности условно-категорического силлогизма:

от отрицания истинности основания к отрицанию истинности следствия

А® В, не-А

не-В

и от утверждения истинности следствия к утверждению истинности основания.

А® В, В

А

Однако заключение по этим модусам будет вероятностным, а не достоверным. Основание и следствие нельзя поменять местами. Например, высказывание «Если вещество - металл, то оно электропроводно» является верным, т.к. все металлы - это электропроводники (из того, что вещество - металл, с необходимостью вытекает его электропроводность). Однако, высказывание: «Если вещество электропроводно, то он - металл», неверно, т.к. не все электропроводники являются металлами (из того, что вещество электропроводно, не вытекает то, что оно - металл). Эта особенность обуславливает два правила условно-категорического умозаключения.

РАЗДЕЛИТЕЛЬНЫЙ СИЛЛОГИЗМ

Силлогизм, в котором по крайней мере одна из посылок – разделительное суждение (дизъюнкция), называется разделительным. Каждый член разделительного суждения называется альтернативой.

Разделительно-категорические силлогизмы имеют два правильных модуса: утверждающе-отрицающий и отрицающе-утверждающий.

В утверждающе-отрицающем модусе (modus ponendo tollens) первая посылка представляет собой строгую дизъюнкцию нескольких вариантов чего-либо, во второй посылке утверждается один из них, а в выводе отрицаются все остальные (таким образом, рассуждение движется от утверждения к отрицанию).

Например:

Углы бывают либо острые, либо тупые, либо прямые.

Данный угол - oстрый.

Следовательно, данный угол не является ни тупым, ни прямым.

Этот силлогизм имеет схему:

A v B v С, A

не-B и не-С

Правило modus ponendo tollens - разделительная посылка обязательно должна быть строгой дизъюнкцией, т.е. необходимо, чтобы члены де­ления исключали друг друга. Из соединительно-разделительной посылки вывод по этому модусу с необходимостью не следует.

Например:

Это преступление совершил О., или П., или Р.

Это преступление совершил О.

Нельзя с необходимостью сказать, что это преступление не совершили ни П., ни Р. Действительно, преступление могли, например, совершить O., П. и Р. в соучастии.

В умозаключении по отрицающе-yтверждающему модусу (modus tollendo ponens) производится утверждение посредством отрицания.

Например:

Приговор суда может быть или обвинительным или оправдательным.

Приговор суда по данному делу не является обвинительным.

Следовательно, он является оправдательным.

Этот силлогизм имеет схему:

A v B, не-A

B

Во второй посылке отрицаются все члены дизъюнкции, за исключением одного, который утверждается в заключении. Правило modus tollendo ponens - в разделительной посылкe должны быть перечислены все возможные альтернативы.

Например:

Смерть могла наступить в результате убийства или в результате самоубийства.

Смерть не могла наступить в результате самоубийства.

Нельзя сказать, что смерть произошла в результате убийства, т.к. она могла произойти в результате несчастного случая.

УСЛОВНО-РАЗДЕЛИТЕЛЬНЫЙ СИЛЛОГИЗМ

В условно-разделительных силлогизмах одна посылка является условным суждением, а другая – разделительным. В зависимости от того, сколько следствий установлено в условной посылке, различают дилеммы, трилеммы, полилеммы.

Лемма – означает по-гречески предложение. В выводе такого умозаключения утверждается альтернатива, т. е. необходимость выбора только одного из всех возможных предложений.

Таким образом, дилемма – это условно-разделительное умозаключение с двумя альтернативами. Различают следующие виды дилемм: простые и сложные, конструктивные и деструктивные.

Простая конструктивная дилемма строится по схеме:

А® В

С® В

A v С

В

Например:

Если у больного болит зуб, рекомендуется принять обезболивающее.

Если у больного болит голова, также рекомендуется принять обезболивающее.

В данном случае болит либо зуб, либо голова.

Больному рекомендуется принять обезболивающее.

Сложная конструктивная дилемма отличается от простой тем, что оба следствия из условной посылки различны.

А® В

С® D

A v С

В v D

Пример (рассуждение Штирлица из книги Ю. Семенова «Семнадцать мгновений весны»):

Если я вернусь в Берлин, меня могут схватить в гестапо.

Если возвращусь в Москву, не выполню до конца задание.

Я могу либо ехать в Берлин, либо возвратиться в Москву.

Меня могут схватить в гестапо, либо я не выполню до конца задание

Простая деструктивная дилемма содержит одну посылку, состоящую из двух условных суждений, в которых из одного и того же основания вытекают два различных следствия; вторая посылка представляет собой дизъюнкцию отрицания обоих следствий; в заключении отрицается основание. Ее схема:

А® В

А® С

не-В v не-С

не-А

Например:

Если человек болен тифом, то у него будет высокая температура и появится сыпь.

У больного нет высокой температуры, либо нет сыпи.

Значит, человек не болен тифом.

Сложная деструктивная дилемма содержит одну посылку, состоящую из двух условных суждений с разными основаниями и разными следствиями; вторая посылка есть дизъюнкция отрицаний обоих следствий; заключение является дизъюнкцией отрицаний обоих оснований. Ее схема:

А® С

В® D

не-C v не-D

не-A v не-B

Например:

Если студент знает материал, то он может привести доказательства.

Если студент понимает, то сможет решить задачу.

Студент либо не может привести доказательства, либо не может решить задачу.

Значит, он либо не знает, либо не понимает материал.

Источником ошибок является чаще всего неполное пе­речисление членов деления. Двумя альтернативами иногда нельзя исчерпать всего возможного числа случаев. Весьма часто дилемму строят таким образом, что из всех возможных альтернатив берут только две альтернативы, вследствие чего и получается ошибка.

Например:

Если какой-либо ученик любит учиться, то он не нуждается ни в каком поощрении.

Если же он чувствует отвращение к учению, то всякое поощрение окажется бесполезным.

Ученик может или любить учение, или чувствовать к нему отвращение.

Следовательно, поощрение или излишне, или бесполезно в деле обучения.

Эта дилемма ложна, потому что «любовь к учению» и «отвра­щение к учению» не суть единственно возможные альтернативы, так как могут быть такие ученики, которые не питают любви к учению, но не питают и отвращения к нему; для таких учеников поощрение может быть действительным.

ДОКАЗАТЕЛЬСТВО И ОПРОВЕРЖЕНИЕ

Доказательство - логическая операция по обоснованию истинности суждения с помощью других суждений, истинность которых уже доказана.

Во всяком доказательстве различают тезис, основания (аргументы, доводы) и демонстрацию (форму доказательства).

Тезисом называется суждение, истинность которого требуется доказать.

Основаниями (аргументами, доводами) называются истинные суждения, с помощью которых обосновывается тезис. Основаниями могут быть суждения об удостоверенных фактах, определения, аксиомы, доказанные ранее положения науки (законы, теоремы и т.д.)

Демонстрация – логическая форма построения доказательства. Демонстрация может принимать форму различных умозаключений.

ВИДЫ ДОКАЗАТЕЛЬСТВА

Прямым называется доказательство, при котором истинность выдвинутого тезиса логически следует из оснований (аргументов). При прямом доказательстве берутся такие основания, которые являются достаточными для обоснования тезиса.

Косвенным называется доказательство, при котором истинность выдвинутого тезиса обосновывается путем доказательства ложности антитезиса.

Косвенные доказательства широко используются в так называемых «точных» науках, где оно носит название «доказательства от противного». Наиболее распространенными видами косвенного доказательства являются апогогическое и разделительное доказательства.

При апогогическом доказательстве ложность антитезиса устанавливается следующим образом: предполагается истинность антитезиса и из него выводятся следствия. Если хотя бы одно из полученных следствий вступает в противоречие с имеющимися суждениями, истинность которых уже установлена, то следствие признается ложным, а вслед за ним признается ложность антитезиса.

При разделительном доказательстве устанавливается ложность всех членов разделительного суждения, кроме одного, являющегося доказываемым тезисом. Разделительное доказательство строится по отрицающе-утверждающему модусу разделительно-категорического силлогизма.

Опровержение - это логический процесс обоснования ложности выдвинутого положения. Опровержение является частным случаем доказательства.

Различают следующие виды опровержения:

а) опровержение тезиса

б) опровержение аргументов

в) опровержение связи тезиса с аргументами.

ПРАВИЛА ДОКАЗАТЕЛЬСТВА И ОПРОВЕРЖЕНИЯ

Основные элементы доказательства и опровержения - тезис, аргументы, демонстрация - подчиняются логическим правилам, нарушение которых ведет к ошибкам.

Логические ошибки могут быть преднамеренными (софизмы) и непреднамеренными (паралогизмы).

Правила тезисов

1. Тезис должен быть ясно и четко сформулирован.

Ошибка:

выдвижение неопределенного, неясного, неточного тезиса. Кто слишком много доказывает, тот ничего не доказывает.

2. Тезис должен оставаться неизменным на протяжении всего доказательства.

Ошибка:

«подмена тезиса» - заключается в том, что доказывается или опровергается не выдвинутый в начале доказательства тезис, а абсолютно новое положение.

Правила аргументов

1. Аргументы должны быть истинными, доказанными суждениями.

Ошибка:

а) «ложное основание» или «основное заблуждение» - обоснование тезиса ложными аргументами;

б) «предвосхищение основания» - в качестве аргументов используются положения, которые сами нуждаются в доказательстве.

2. Аргументами доказательства и опровержения должны быть суждения, истинность которых установлена независимо от тезиса.

Ошибка:

«круг в доказательстве» или «порочный круг» - тезис обосновывается аргументами, а аргументы тезисом.

3. Аргументы должны быть достаточными для данного тезиса.

Ошибка:

а) «мнимое следование» - в качестве аргументов используются положения достоверные, но недостаточные для данного тезиса;

б) «довод к личности» - обоснование истинности или ложности выдвинутого тезиса подменяется положительной или отрицательной оценкой личностных качеств человека, выдвинувшeгo тезис;

в) «довод к публике» - вместо обоснования истинности или ложности выдвинутогo тезиса стремятся повлиять на чувства людей, чтобы они поверили в eгo истинность или ложность без доказательства по существу.