МОУ ГИМНАЗИЯ «ЛАБОРАТОРИЯ САЛАХОВА»
ФОРМАЛЬНАЯ ЛОГИКА
ПОСОБИЕ ДЛЯ УЧАЩИХСЯ 9 КЛАССА
СОСТАВИТЕЛЬ: БОБЕЙКО Т.С.
СУРГУТ
2010
ВВЕДЕНИЕ.
Логику можно называть наукой о формах мысли. В любой области деятельности, как только возникают недоразумения или споры, приходится обращаться к строгому, точному анализу, к логике. Овладеть правилами и законами логики под силу любому, если проявить достаточно упорства и настойчивости. Признаком хорошего изучения любой темы является то, что усвоенные логические операции проделываются в голове подсознательно, полуавтоматически. Поэтому при изучении данного предмета желательно делать как можно больше упражнений.
ПОНЯТИЕ
Мысли выражаются словами. Логика превращает слова в понятия. "Бытие", "живая клетка", "рекорд в парусных гонках" - все это разные понятия.
Первое, что отличает понятие от слова или выражения, - это однозначность. Многие слова имеют по несколько значений. В поэзии часто специально подыскивают слова, способные вместить в себя много разных оттенков смысла. Для логики подобное обращение со словами недопустимо. В каждое понятие должно быть вложено одно единственное значение, оно должно соответствовать только одному предмету или одному классу. Обозначение предметов требует выделения в них каких-то определенных признаков, которых в любой вещи бесконечно много. Например, квадрат можно назвать и ромбом с прямыми углами, и прямоугольником с равными сторонами. Среди всего этого многообразия надо выбирать свойства наиболее типичные, характерные для данного рода вещей.
Таким образом, понятие – это форма мысли, отражающая предметы в их существенных и общих признаках.
СОДЕРЖАНИЕ И ОБЪЕМ ПОНЯТИЙ
Каждое понятие имеет содержание и объем.
Содержание понятия - это наиболее важные признаки объекта, который обозначен этим понятием.
Например, чтобы установить содержание понятия «человек», надо указать такой признак, который является наиболее важным, главным, основным для человека, признак, который отличает его от всех других существ, объектов, предметов и вещей. Таким признаком является наличие у человека разума. Следовательно, в содержание понятия «человек» входит только один важный признак — наличие разума.
А в содержание понятия «мужчина» входит уже два важных признака: 1) наличие разума (потому что любой мужчина — это человек); 2) принадлежность к определенному полу.
А если надо установить содержание понятия «русский мужчина», то следует указать три важных признака: 1) наличие разума; 2) принадлежность к определенному полу; 3) принадлежность к определенной национальности.
Объем понятия - это количество объектов, охватываемых этим понятием.
Например, объем понятия «человек» шире, чем объем понятия «мужчина», потому что людей существует больше, чем мужчин. А объем понятия «русский мужчина» меньше, чем объем понятия «мужчина», потому что русских мужчин на свете намного меньше, чем вообще всех мужчин. И, наконец, объем понятия «первый президент России» равен единице, потому что включает в себя только одного человека.
Точно так же объем понятия «город» является очень широким в силу того, что это понятие охватывает собой все множество городов, какие только существуют на свете, а объем понятия «столица» меньше объема понятия «город», так как это понятие охватывает собой только столицы (которых намного меньше, чем городов). Объем же понятия «столица России» равен единице, потому что включает в себя один единственный город.
В логике давно было отмечена связь объема и содержания. Кратко этот закон формулируется так: чем шире содержание, тем меньше объем и наоборот.
Следует помнить: закон обратного отношения выполняется только при последовательном добавлении признаков. Простая замена их не создает указанной закономерности. Так, цепочка понятий "черная собака", "овчарка", "дрессированная собака" не образует ни линии ограничения, ни линии обобщения. Другое дело, если взять такую последовательность: "собака", "овчарка", "черная овчарка", "черная дрессированная овчарка". Здесь признаки наслаиваются один на другой, и объем шаг от шага делается меньше.
ВИДЫ ПОНЯТИЙ
В зависимости от объема понятия могут быть единичными, общими, пустыми.
Общими называются понятия, объемы которых включают множество однородных предметов (явлений, событий). Даже если в объеме только два явления или две вещи, то этого достаточно, чтобы охватывающее их понятие считать общим. Так, "полюс Земли" представляет собой общее понятие, хотя полюсов всего два - северный и южный. Тем более общими являются понятия "книга", "ракета", "морское млекопитающее" - в объеме каждого из них далеко не один предмет.
Единичными называются понятия, объемы которых включают только один предмет (явление, событие). Таковы «Атлантический океан», «атомный ледокол», «Ленин», «Эйфелева башня», «самый большой город в мире», «Царь-пушка» и другие.
Пустыми называются понятия, объемы которых не включают ни одного предмета (явления, события). Понятие «круглый квадрат», «кентавр» - пустое (или с нулевым объемом), так как в реальности мы не найдем ни одного предмета, который обладал бы признаком «быть круглым квадратом», «быть кентавром».
По объему понятия также бывают собирательными и разделительными. Собирательные понятия обозначают объект, который состоит из какого-то ограниченного набора элементов, распадается на какие-то составные части, например, «10 класс “А”», «рота солдат», «музыкальный коллектив», «волчья стая», «созвездие». Разделительные понятия обозначают объект, который является целым, а не собирается из какого-то ограниченного набора элементов, например, «человек», «растение», «звезда», «океан», «карандаш». Только у разделительных понятий то, что говорится об общем, относится к каждому в отдельности.
Если говорят: «избиратели проголосовали за такого-то кандидата в депутаты», то ясно, что отсюда нельзя делать вывод, будто за него голосовали все. Стало быть, здесь понятие «избиратели» употреблено в собирательном смысле. В другом случае то же самое слово может иметь разделительный смысл, скажем, в высказывании: «Избиратели – совершеннолетние граждане».
В зависимости от содержания понятия могут быть
конкретными и абстрактными
положительными и отрицательными
безотносительными и соотносительными
Конкретными называются понятия, которые обозначают какой-либо объект, например, «стол», «гора», «дерево», «планета».
Абстрактными называются понятия, которые обозначают не объект, а признак, свойство, например, «мужество», «глупость», «неряшливость», «темнота».
Положительными называются понятия, которые обозначают наличие какого-либо признака, например: «животное», «школа», «небоскреб», «комета».
Отрицательными называются понятия, обозначающие отсутствие признака, например: «не животное», «не школа», «неправда», «бестактность». Легко заметить, что понятие является отрицательным, когда слово, которым оно выражено, употребляется с частицей не или без, однако, если эта частица входит в состав слова, которое без нее не употребляется, например, «неряшливость», «ненастье», «нерадивость», «невежество», то понятие, выраженное таким словом, является положительным.
Безотносительные понятия описывают предметы, существующие раздельно и потому воспринимаемые вне связи с другими предметами. В содержании таких понятий нет указания на отношение к другим предметам, например: «дерево», «государство», «книга».
В соотносительных понятиях отражаются предметы, существующие только взаимосвязано и одновременно друг с другом и поэтому не мыслящиеся одно без другого, например, понятие «родители» и «дети», «начальник» и «подчиненный», «причина и следствие», «восход» и «закат», «учитель» и «ученик».
Учитель, у которого нет и не было учеников, никак не может считаться учителем; равным образом и учеников без учителя не бывает. Также нерасторжимо связаны и другие пары. Конечно, можно отвлечься от того, что у причины есть следствия, но тогда она не причина, а просто событие. И отец может, разумеется, существовать и вне связи с сыном, но тогда он не отец, а мужчина вообще.
Любому понятию можно дать логическую характеристику. Это значит охарактеризовать его по объему и содержанию.
Например, понятие «Солнце» - единичное (потому что в его объем входит только один объект, одно небесное тело), разделительное (так как Солнце не состоит ни из каких частей, не делится на них), конкретное (ведь Солнце - это объект, а не признак или свойство), положительное (потому что этим понятием обозначается наличие, а не отсутствие объекта), безотносительное.
ОТНОШЕНИЯ МЕЖДУ ОБЪЕМАМИ ПОНЯТИЙ
Классификация понятий с точки зрения взаимоотношений между ними начинается с разделения их на сравнимые, которым свойственны чисто логические связи и отношения, и несравнимые, у которых таких связей нет вообще.
К несравнимым относятся, например, "трамвай" и "треугольник", "осень" и "обратная сторона Луны", "алмаз" и "паровозный гудок". Их отличительная черта состоит в том, что ни в их содержании, ни в их объеме нет общих элементов. Они обязательно имеются у сравнимых понятий, потому что у них есть общие элементы в объеме и (или) содержании.
Сравнимые понятия делятся на два вида - совместимые и несовместимые, а каждый из этих в свою очередь распадается еще на три разновидности.
Совместимые понятия - это такие понятия, объемы которых полностью или частично совпадают. Например, понятия «спортсмен» и «американец» являются совместимыми, т.к. их объемы имеют общие объекты: есть такие спортсмены, которые являются американцами и, наоборот, есть такие американцы, которые являются спортсменами.
Несовместимые - это такие понятия, объемы которых не совпадают. Например, понятия «треугольник» и «квадрат» являются несовместимыми, потому что их объемы не имеют общих элементов: ни один треугольник не может быть квадратом, и наоборот.
Между совместимыми понятиями могут быть отношения:
тождества или равнозначности
пересечения или частичного совпадения объемов
подчинения
Между несовместимыми понятиями:
соподчинения
противоположности
противоречия
Для иллюстрации отношений между объемами понятий применяются круговые схемы, впервые введенные Эйлером.
1. В отношении равнозначности находятся понятия, в которых мыслится один и тот же предмет. Объемы этих понятий полностью совпадают. Например, «человек» и «разумное существо, умеющее абстрактно мыслить». Эти понятия равны по своему объему, так как обозначают один и тот же класс - людей. Так отношение равнозначности между понятиями «квадрат» и «равносторонний прямоугольник» изображается схемой, на которой два круга, обозначающие два равных объема, полностью совпадают:
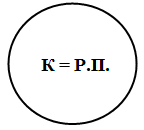
2. В отношении пересечения находятся понятия, чьи объемы совпадают только частично. Например, пересекающимися будут понятия «школьник» и «спортсмен»: есть такие школьники, которые являются спортсменами, и есть такие спортсмены, которые являются школьниками; но в то же время школьник может не быть спортсменом, так же, как и спортсмен может не быть школьником. На схеме Эйлера отношение пересечения изображается двумя пересекающимися кругами (заштрихованная часть показывает частично совпадающие объемы двух понятий):
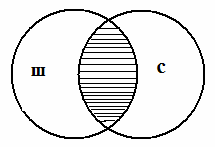
3. В отношении подчинения находятся понятия, одно из которых полностью входит в объем другого. Например, в отношении подчинения находятся понятия «карась»
и «рыба», т.к. все караси — это обязательно рыбы, но рыбами являются не только караси, есть и другие виды рыб. Таким образом, объем понятия «карась» является меньшим по отношению к объему понятия «рыба» и полностью в него включается (подчиняется ему). На схеме Эйлера отношение подчинения изображается двумя кругами, один из которых располагается внутри другого:
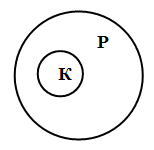
4. Понятия находятся в отношении соподчинения тогда, когда их объемы не имеют общих элементов, но в то же время входят в объем какого-то третьего понятия, родового для них (совместно ему подчиняются). Например, понятия «сосна» и «береза» являются соподчиненными: ни одна сосна не может быть березой, и наоборот, но и множество всех сосен, и множество всех берез включается в более широкий объем понятия «дерево». На схеме Эйлера отношение соподчинения изображается двумя несоприкасающимися кругами:
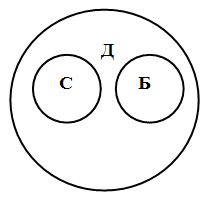
5. Понятия находятся в отношении противоположности в том случае, если они обозначают какие-то взаимоисключающие признаки, крайние состояния чего-либо, между которыми, однако, всегда есть некий средний, переходный вариант. Например, противоположными являются понятия «высокий человек» и «низкий человек» (третьим или переходным вариантом между ними будет понятие «человек среднего роста»). На схеме Эйлера отношение противоположности изображается двумя несоприкасающимся кругами, которые находятся как бы на разных «полюсах»:
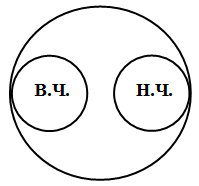
Поскольку объемы противоположных понятий не соприкасаются, это отношение отчасти похоже на соподчинение. Однако понятия, находящиеся в отношении соподчинения, обозначают просто различные объекты разных видов и одного рода, но не противоположные друг другу. Не можем же мы утверждать, что сосна является противоположностью березы, а береза — противоположностью сосны: это просто разные деревья, и не более того.
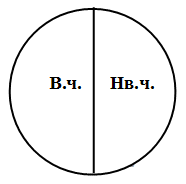
6. Понятия находятся в отношении противоречия, если одно из них представляет собой отрицание другого, причем в отличие от противоположных понятий, между противоречащими понятиями никак не может быть третьего или среднего варианта. Например, в отношении противоречия находятся понятия «высокий человек» и «невысокий человек». В том случае, когда одно понятие является отрицанием другого, третий вариант автоматически исключается: и «низкий человек», и «человек среднего роста» — это «невысокий человек». На схеме Эйлера отношение противоречия изображается одним кругом, поделенным на две части, которые обозначают противоречащие понятия:
ЛОГИЧЕСКИЕ ОПЕРАЦИИ НАД ПОНЯТИЯМИ
Логические операции над понятиями:
обобщение
ограничение
определение
деление
Обобщить понятие – значит перейти от понятия с меньшим объемом, но с большим содержанием к понятию с большим объемом, но с меньшим содержанием. Пределом обобщения являются понятия с наиболее широким объемом – категории (материя, сознание). Категории не имеют рода, поэтому их обобщить нельзя.
Ограничить понятие – значит перейти от понятия с большим объемом, но с меньшим содержанием к понятию с меньшим объемом, но с большим содержанием.
Определением называется логическая операция, позволяющая отличать изучаемый предмет от других предметов, установить значение того или иного слова или термина.
Для достижения точности и полной ясности в выводах, доказательствах, при анализе высказываний и тем более в спорах определения совершенно необходимы. Нельзя было бы создать ни одной теории без строго определенных понятий и категорий. Ими обязательно пользуется каждая наука.
Определения бывают явными и неявными. Во всяком явном определении есть определяемое понятие и определяющая часть.
В зависимости от того, что определяется, выделяются реальные и номинальные определения. Номинальное – определение, посредством которого формулируется значение некоторого термина. Например, «термином «пятиугольник» обозначается «многоугольник с пятью сторонами». Реальное – определение, с помощью которого предмет выделяется среди других предметов по некоторому отличительному признаку. Например, «человек – разумное животное». Вид реального определения – определение через род и видовое отличие, т.е. через указание на совокупность предметов, среди которых выделяется предмет и признак, при помощи которого определяемый предмет отличается от сходных с ним. Например, «барометр есть метеорологический прибор, служащий для измерения атмосферного давления». Определение, указывающее на способ образования в приведенном примере определения через «род» (родовым признаком) будет «метеорологический прибор», а видовым отличием «служащий для измерения атмосферного давления».
В практике повседневной жизни и в науке мы очень часто пользуемся так называемыми неявными определениями. Особенность их состоит в том, что определение предмета происходит посредством указания на его отношение к другим предметам.
Виды неявных определений
Семантическое - определение, в котором определенному обозначению непосредственно ставится в соответствие предмет, описанный через его отличительные признаки.
Например, выражение «домашние животные» применимо в отношении и коров, и лошадей, и кошек, и собак, и т.д.
Синтаксическим называется определение, в котором предмет определяется через правила оперирования с ним. Например, «0 - такое число, которое, будучи умножено на любое другое число, дает 0».
Остенсивными называются определения значения слов путем непосредственного показа, демонстрации предметов, которые эти слова обозначают. С таким процессом мы встречаемся в процессе обучения иностранному языку. Учитель показывает учащимся предметы, называя их.
В контекстуальных определениях определение предмета сводится к определению контекста, в котором он фигурирует. Таким способом можно определять служебные грамматические слова.
Правила определения: