2.2 Исследование функции полезности
Данная функция полезности компоненты РИС в нормированном виде имеет вид:
где
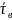и
- постоянные времени «восхода» и «заката»
компоненты системы.
Следует
заметить, что текущее время t
и параметры
,
пронормированы по средней продолжительности
жизни компоненты
,
т.е.
,
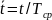и
Введём замену констант для упрощения выражения и последующих расчётов:
и
.
Тогда выражение примет вид:
Начнём наше исследование.
.
,
отсюда следует, что функция ни чётная,
ни нечётная.Горизонтальных асимптот нет.
Исследуем на экстремумы и монотонность.
В результате преобразований получаем:
Это значит, что функция не имеет точек экстремума и является монотонно возрастающей.
Исследуем на выпуклость (вогнутость).
В результате преобразований получаем:
Эти
говорит о том, что функция является
вогнутой (выпуклой вниз) на интервале
.
Наклонных асимптот нет.
Построим график при
.
Рис.
3 – График зависимости
.
Разложим функцию полезности в ряд Тейлора.
…
При
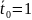получаем:
…
2.2 Исследование функции ущерба
Для начала найдём ущерб по следующей формуле:
Начнём наше исследование.
,
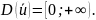
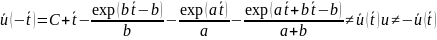отсюда следует, что функция ни чётная,
ни нечётная.Горизонтальных асимптот нет.
Исследуем на экстремумы и монотонность.
По определению интеграла получаем:
Если
возрастает, то есть больше нуля, то
.
Это значит, что функция ущерба монотонно
убывает на интервале
.
,
отсюда следует, что
имеет точку экстремума
.
значит
точка
– точка максимума.
5) Исследуем на выпуклость (вогнутость).
Так
как
Эти говорит о том, что функция является выпуклой вниз на интервале .
Наклонных асимптот нет.
Найдём крутизну K ущерба по следующей формуле:
Таким
образом, крутизна при
в
точке
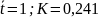
Построим график при
.
Тогда
Рис.
4 - График зависимости
.
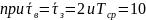Найдём
,
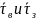при которых ущерб имеет минимальное
значение. Учтём, что
Рис.
5 - График зависимости
Рис.
6 - График зависимости
Рис.
7 - График зависимости
Рис.
8 - График зависимости
Рис.
9 - График зависимости
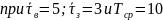
Таким
образом, мы видим, что функция ущерба
минимальна при
.
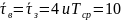Разложим функцию ущерба в ряд Тейлора.
…
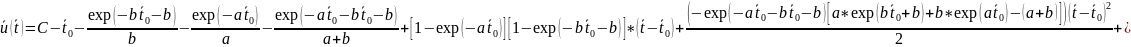При получаем:
…
Заключение
Таким образом, рассмотрев классификацию распределённых информационных систем, исследовав функцию полезности и ущерба, мы приобрели навыки в оценке безопасности систем. В данной курсовой работе также исследована зависимость ущерба от параметров восхода и заката: чем больше параметры, тем меньше ущерб, при том параметры должны быть равны.
Исследование функции полезности и ущерба играет важную роль в оценке безопасности не только РИС, но и всех информационных систем. По полученным данным можно, при известной вероятности ущерба, можно рассчитать риск компьютерно атакуемых информационных систем и технологий. На основе этого предпринимаются различные методы защиты систем.
В будущем, информационные технологии будут сопровождать нас везде, где бы мы ни были, следовательно, возникает необходимость их безопасности, надёжности и жизнестойкости, а чтобы соблюсти данные параметры необходимо провести риск-анализ систем, и наконец, исследовать функцию ущерба. Данное будущее остаётся не только за нами, но и за нашим поколением.