Вариант 21

1. Взаимное расположение прямой и плоскости.

2. Ортогональная классификация кривых 2-го порядка.

3. В аффинной системе координат пространства составить канонические и параметрические уравнения прямой, проходящей через точки 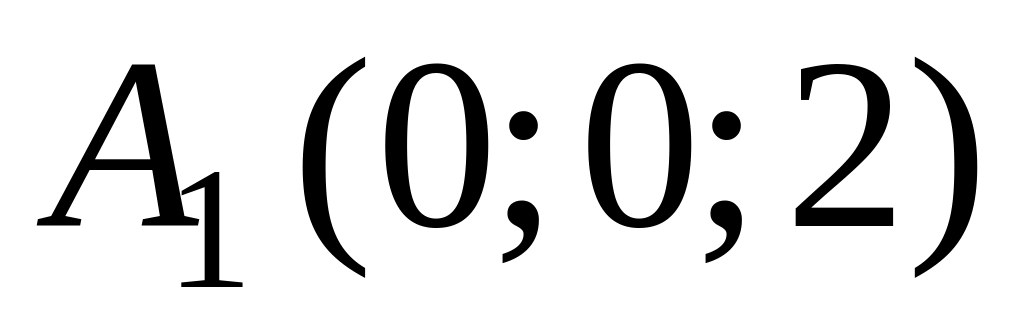и .

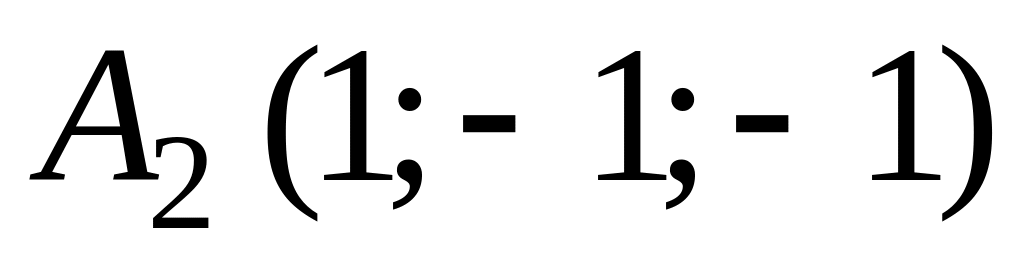4. Найти точки пересечения трех плоскостей, заданных в аффинной системе координат уравнениями , , .

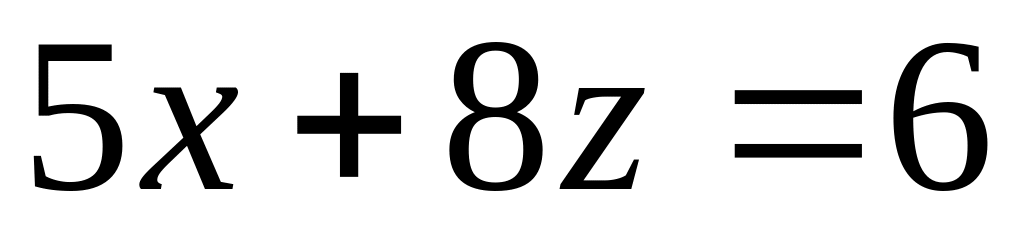5. В ортонормированной системе координат плоскости найти точки эллипса , расстояние от которых до левого фокуса эллипса равно 2,5.

Вариант 22

1. Ортогональные преобразования координат на плоскости.

2. Асимптотические направления для кривых 2-го порядка. Асимптоты гиперболы.

3. В ортонормированной системе координат пространства составить уравнение прямой, проходящей через точку 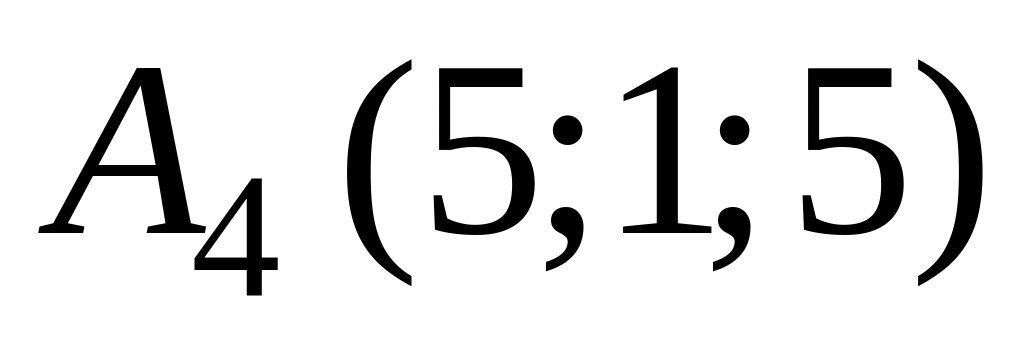перпендикулярно плоскости, содержащей точки , , .

4. Найти точки пересечения трех плоскостей, заданных в аффинной системе координат уравнениями , , .

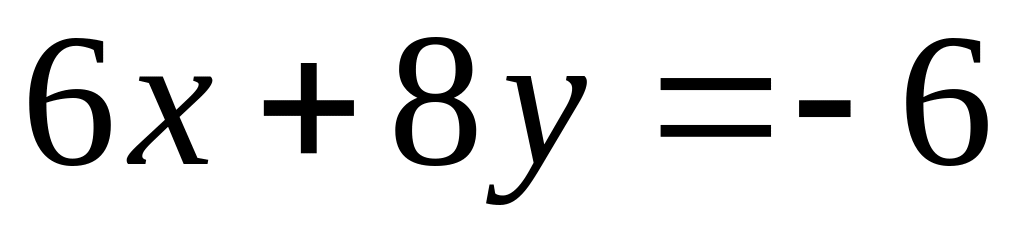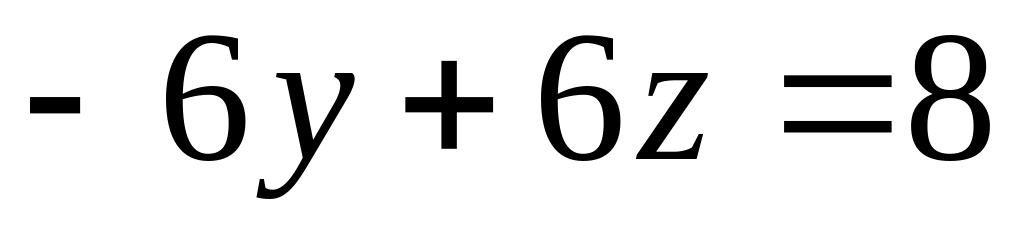5. В ортонормированной системе координат плоскости на параболе найти точки, фокальный радиус которых равен 13.

Вариант 23

1. Ортогональные преобразования координат в пространстве.

2. Центры и центры симметрии кривых 2-го порядка.

3. В ортонормированной системе координат пространства даны точки 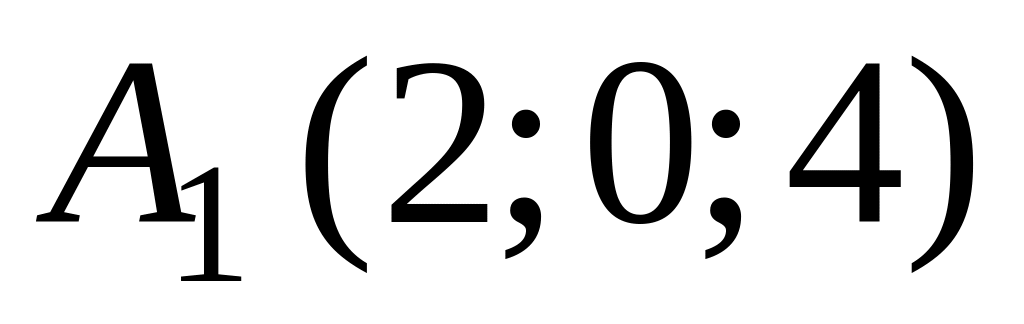, 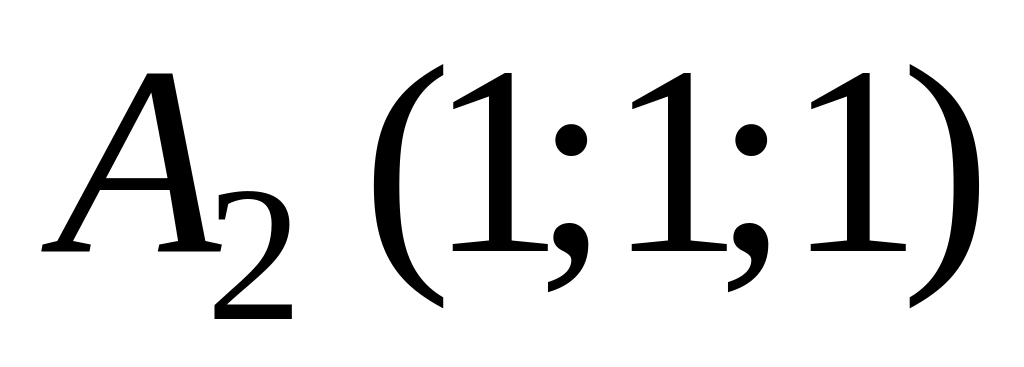. Составить уравнение плоскости, проходящей через точку перпендикулярно прямой .

4. Найти точки пересечения трех плоскостей, заданных в аффинной системе координат уравнениями , , .

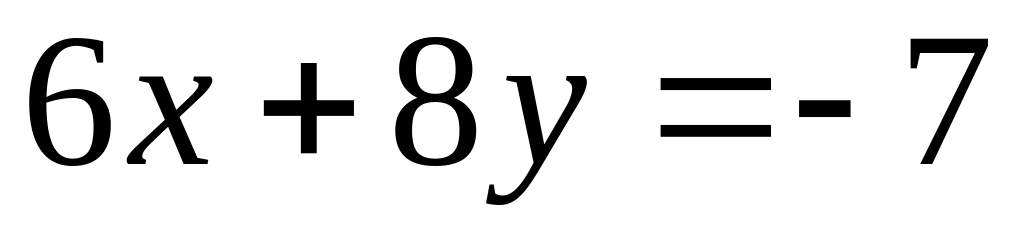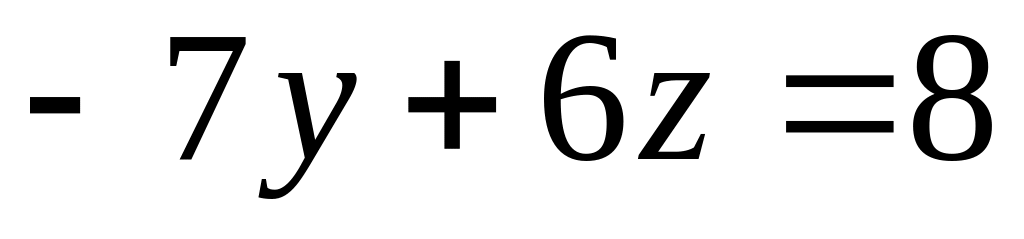5. В аффинной системе координат плоскости составить уравнения касательных к гиперболе , параллельных прямой .

Вариант 24

1. Взаимное расположение двух плоскостей.

2. Цилиндрические поверхности второго порядка.

3. В аффинной системе координат пространства составить уравнение плоскости, проходящей через точки , , .

4. Найти точки пересечения трех плоскостей, заданных в аффинной системе координат уравнениями , , .

5. В аффинной системе координат плоскости составить уравнения касательных к параболе , проведенных из точки .

Вариант 25

1. Преобразования аффинных систем координат.

2. Упрощение уравнения центрального типа кривой 2-го порядка с помощью ортогональных преобразований координат.

3. В ортонормированной системе координат пространства даны точки 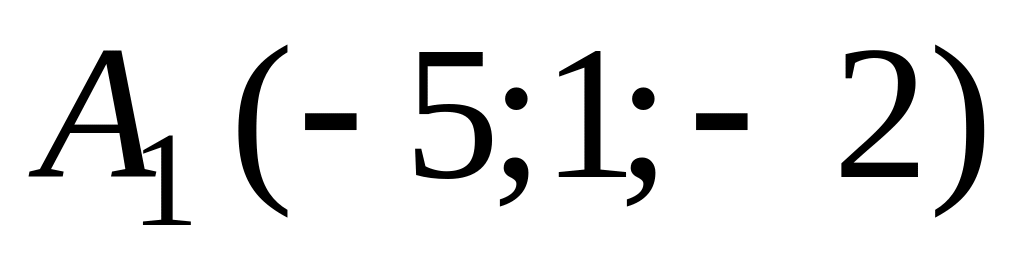, , , 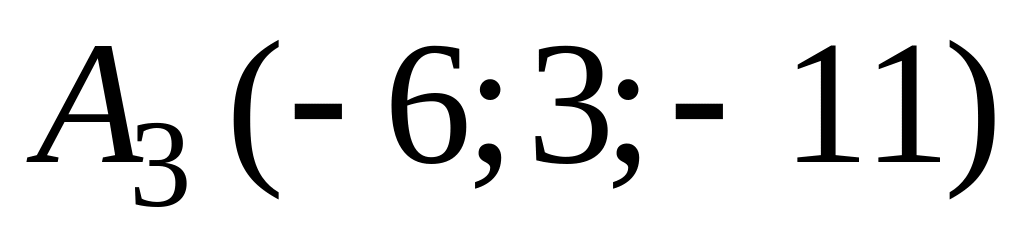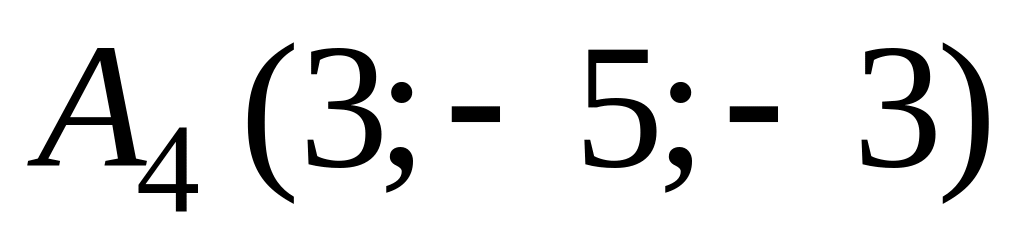. Найти угол между прямой и плоскостью .

4. Найти точки пересечения трех плоскостей, заданных в аффинной системе координат уравнениями , , .

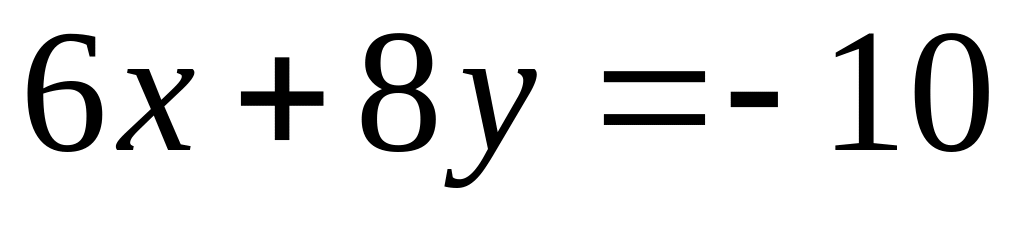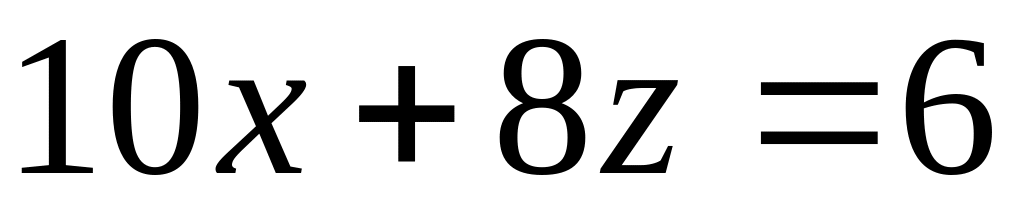5. В ортонормированной системе координат плоскости составить уравнение гиперболы, если ее эксцентриситет , а фокусы совпадают с фокусами эллипса .

Вариант 26

1. Пучок плоскостей.

2. Гиперболический параболоид.

3. В аффинной системе координат пространства составить канонические и параметрические уравнения прямой, проходящей через точки и .

4. Найти точки пересечения трех плоскостей, заданных в аффинной системе координат уравнениями , , .

5. В аффинной системе координат плоскости составить уравнения касательных к эллипсу , параллельных прямой .