МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ТАВРИЧЕСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ им. В.И. ВЕРНАДСКОГО

Факультет _____МАТЕМАТИКИ И ИНФОРМАТИКИ_____________

Кафедра _______ГЕОМЕТРИИ___________________________________

ВОПРОСЫ ВТОРОГО МОДУЛЬНОГО КОНТРОЛЯ

по дисциплине

«Алгебра и геометрия»

для студентов ___1___ курса дневной формы обучения

специальностей ____6.080200 Информатика, Прикладная математика_________

шифр, наименование

образовательно-квалификационного уровня «бакалавр»

Симферополь, 2011

ВАРИАНТ 1

1. Ортогональные преобразования координат на плоскости.

2. Оптическое свойство эллипса.

3. В аффинной системе координат пространства составить канонические и параметрические уравнения прямой, содержащей точки 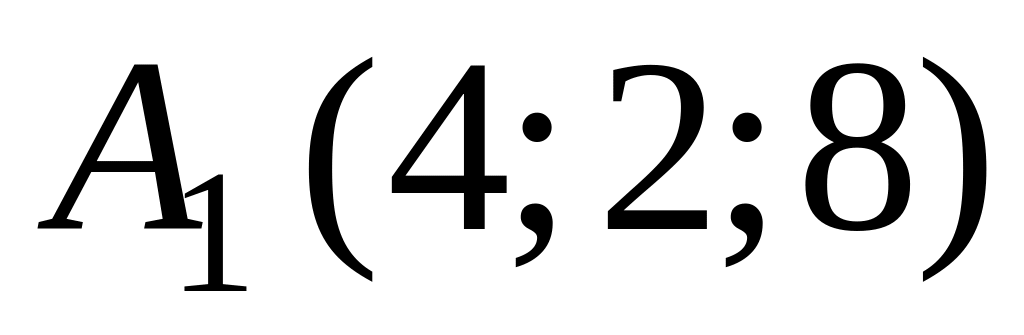и .

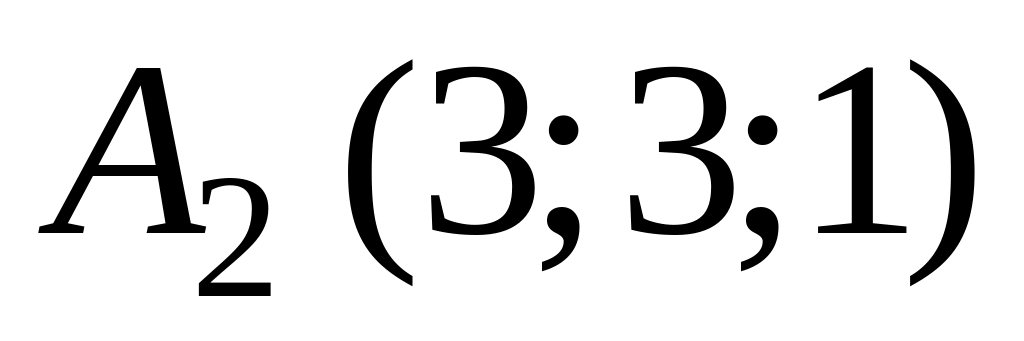4. Найти точки пересечения трех плоскостей, заданных в аффинной системе координат уравнениями , , .

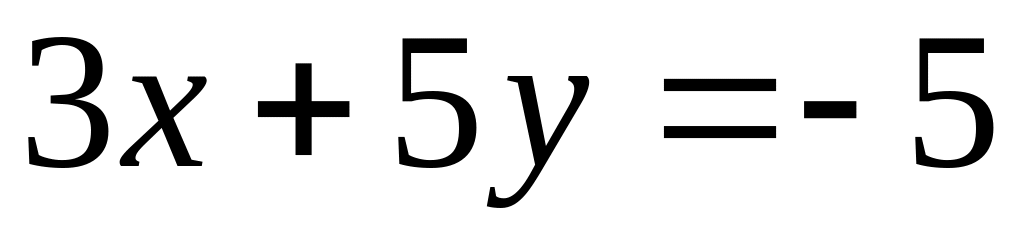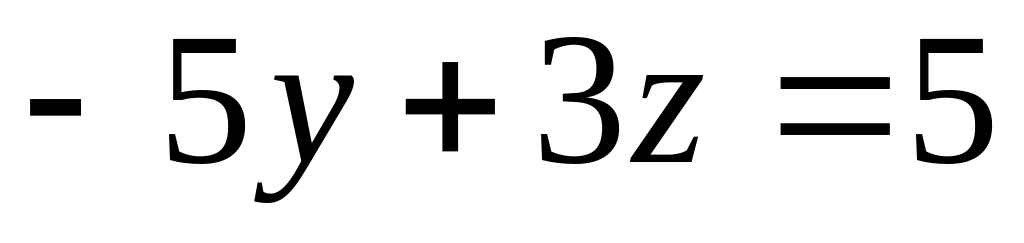5. В ортонормированной системе координат 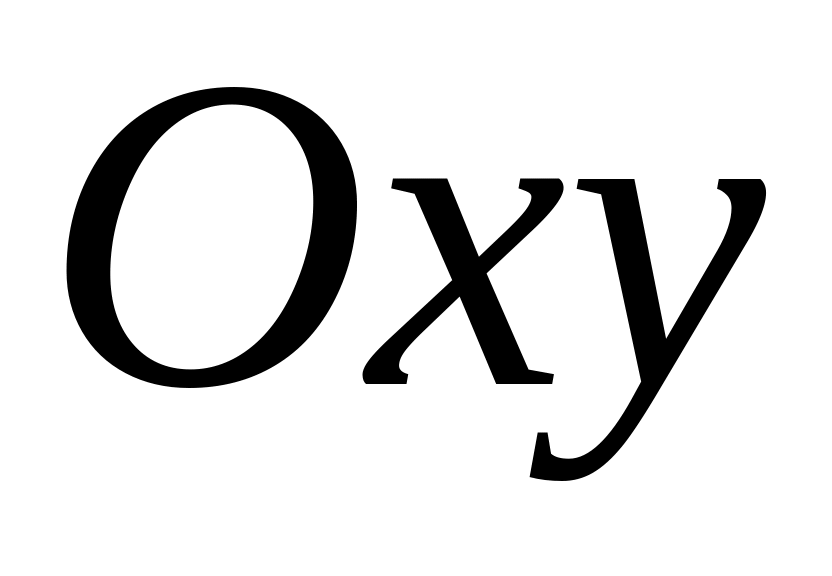плоскости определить точки эллипса 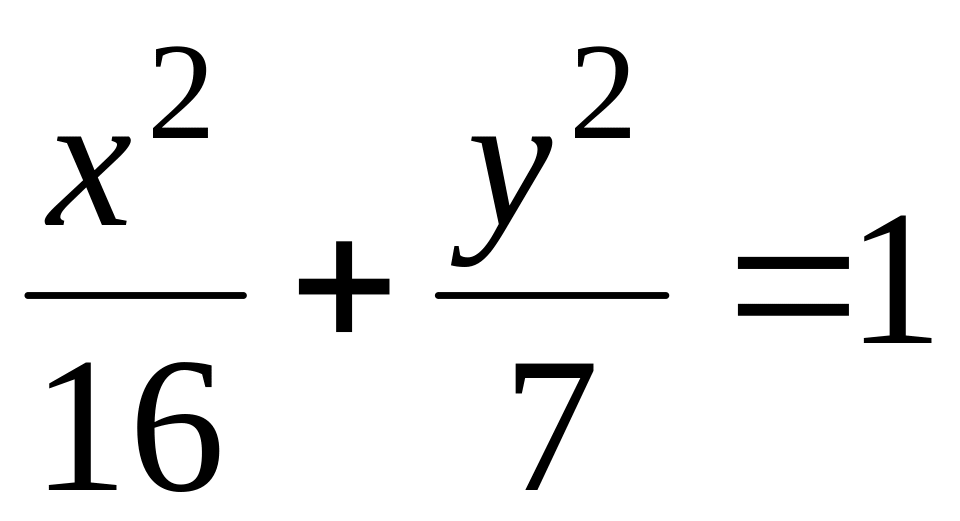, расстояния от которых до его левого фокуса равно 2,5.

Вариант 2

1. Ортогональные преобразования координат в пространстве.

2. Касательная к эллипсу.

3. В аффинной системе координат пространства составить уравнение плоскости, проходящей через точки 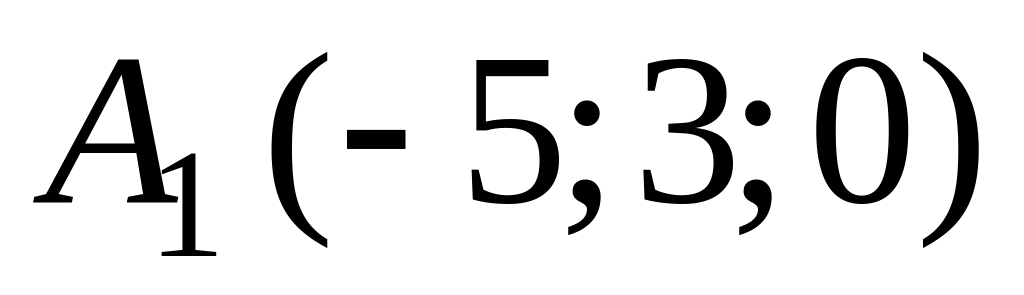, , и .

4. Найти точки пересечения трех плоскостей, заданных в аффинной системе координат уравнениями , , .

5. В ортонормированной системе координат плоскости на параболе 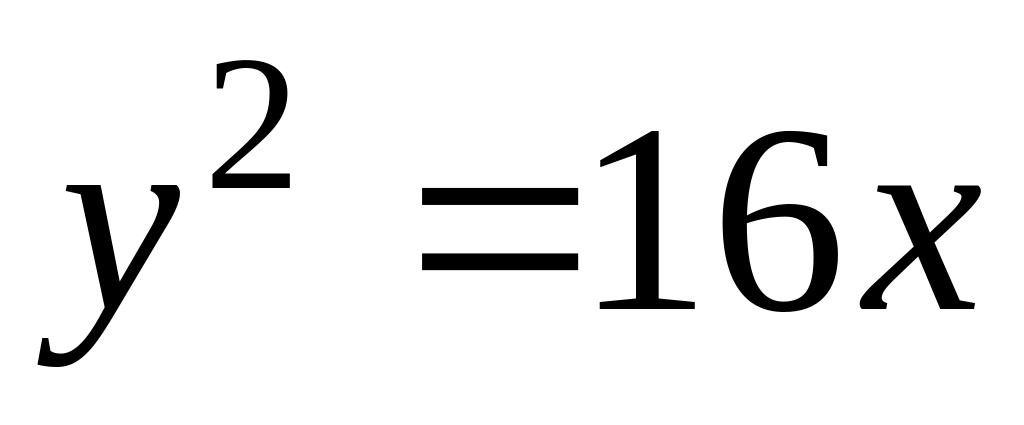найти точки, фокальные радиусы которых равны 13.

Вариант 3

1. Эллипс и его каноническое уравнение.

2. Прямая как пересечение двух плоскостей.

3. В ортонормированной системе координат 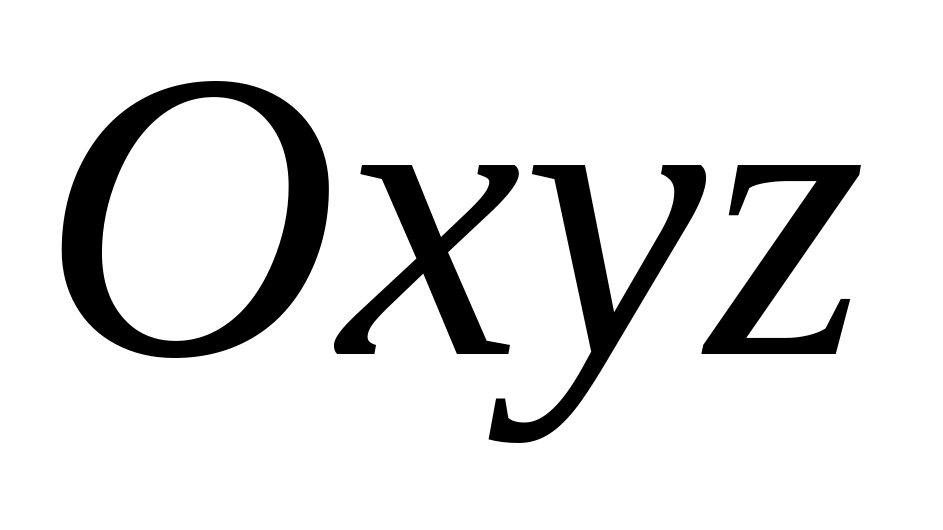пространства даны точки 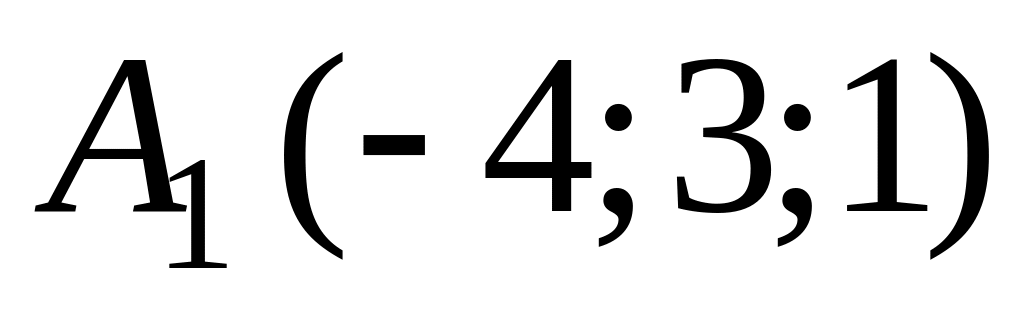, 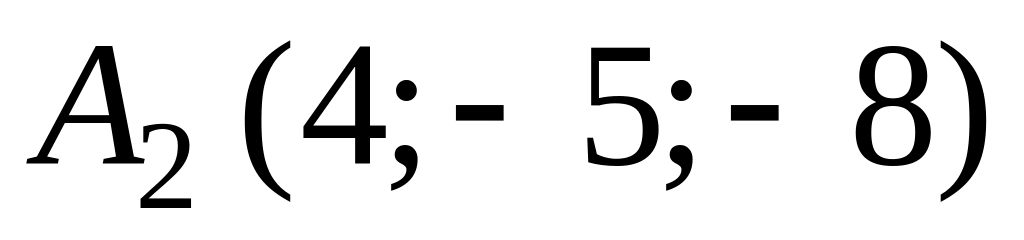. Составить уравнение плоскости, проходящей через точку перпендикулярно прямой .

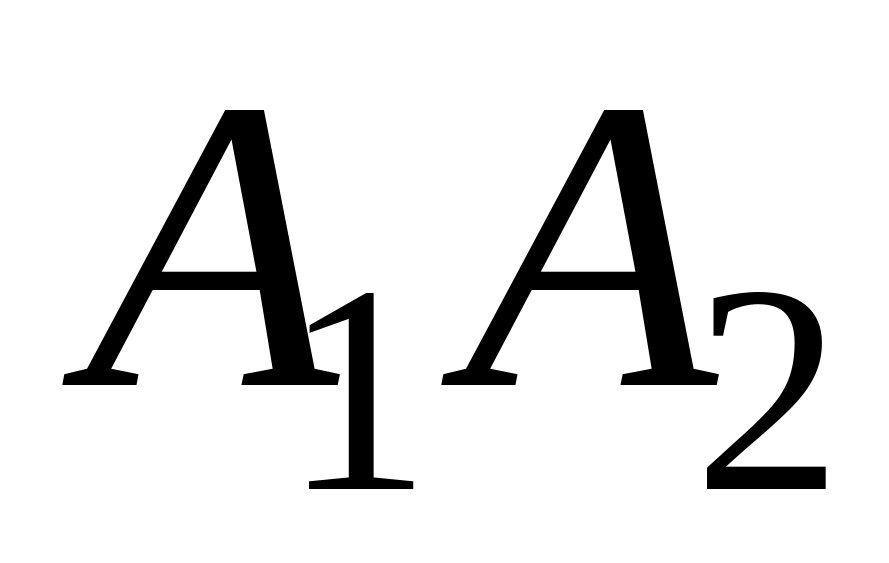4. Найти точки пересечения трех плоскостей, заданных в аффинной системе координат уравнениями , , .

5. В аффинной системе координат плоскости составить уравнения касательных к гиперболе 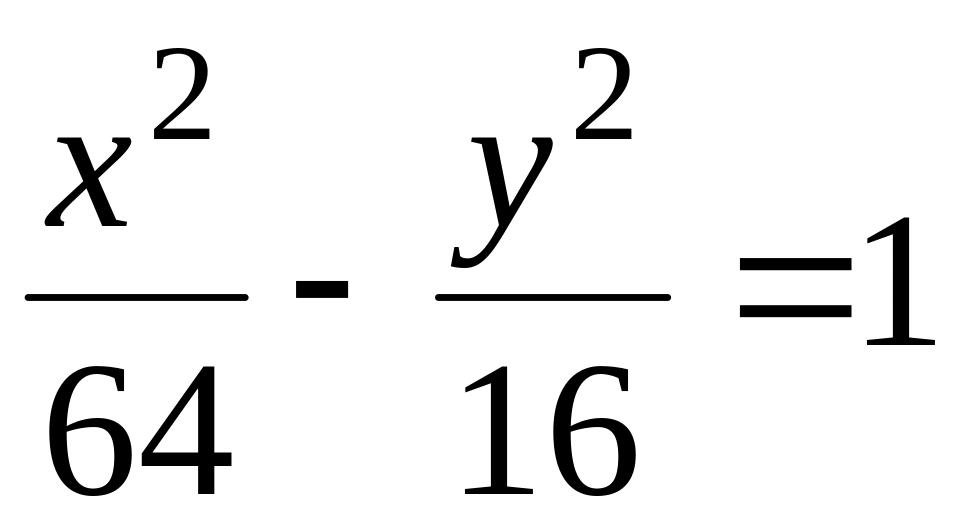, параллельных прямой .

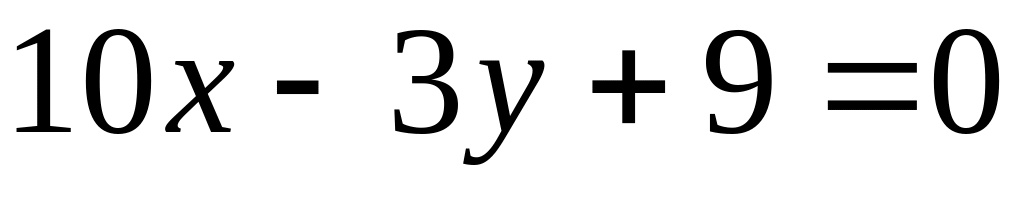Вариант 4

1. Гипербола и ее каноническое уравнение. Равнобочная гипербола.

2. Общее уравнение плоскости.

3. В ортонормированной системе координат пространства даны точки 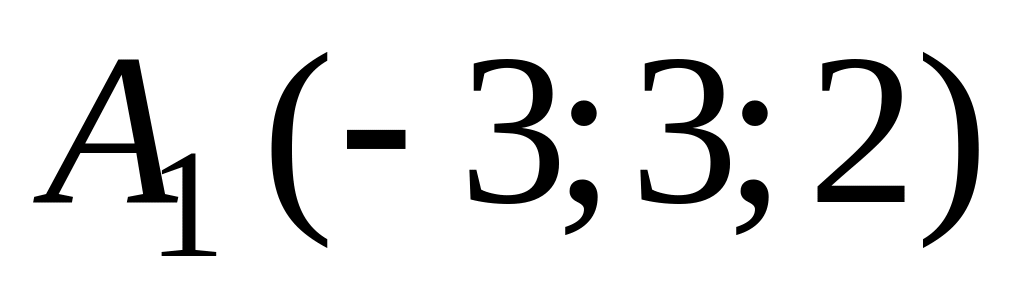, , 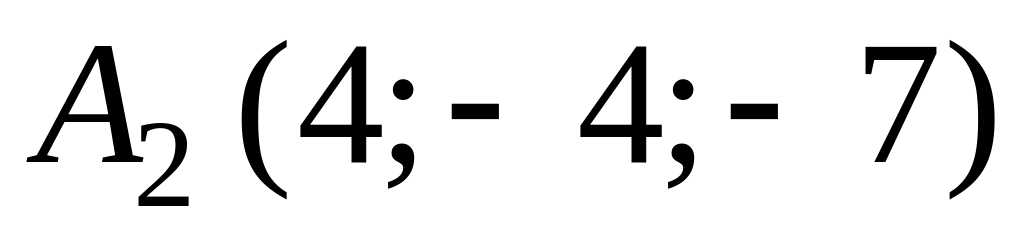, 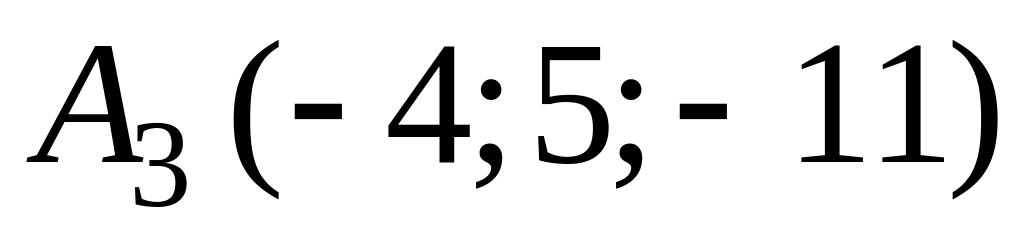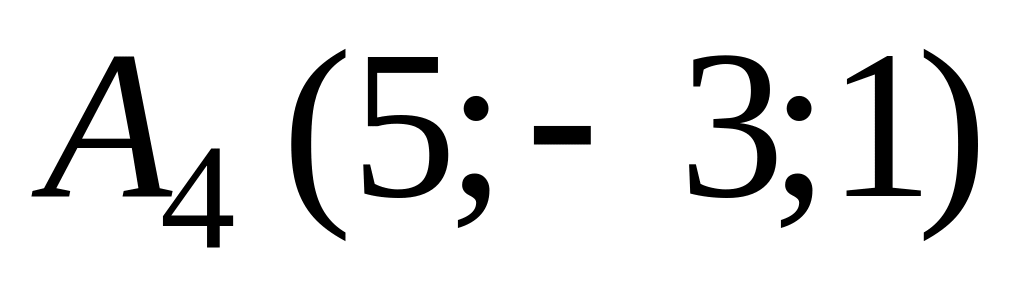. Составить уравнение плоскости, которая содержит прямую 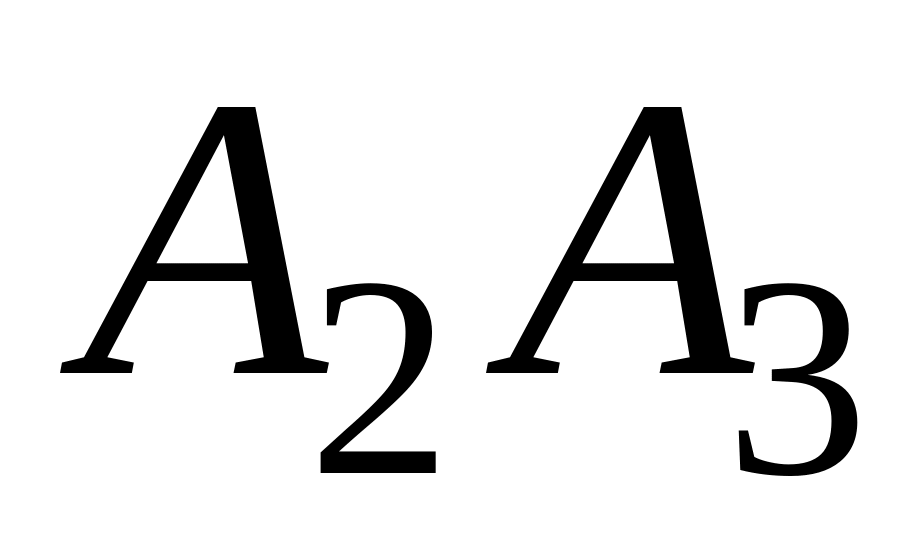и перпендикулярна плоскости .

4. Найти точки пересечения трех плоскостей, заданных в аффинной системе координат уравнениями , , .

5. В ортонормированной системе координат плоскости задан эллипс 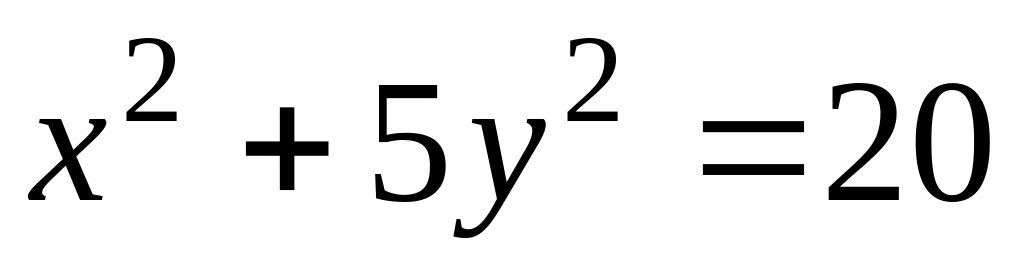. Вычислить площадь четырехугольника, две вершины которого − фокусы этого эллипса, а две другие − вершины эллипса.

Вариант 5

1. Уравнение плоскости, проходящей через данную точку параллельно двум данным векторам.

2. Ортогональные преобразования координат на плоскости.

3. В аффинной системе координат пространства составить уравнение плоскости, проходящей через точки , , .

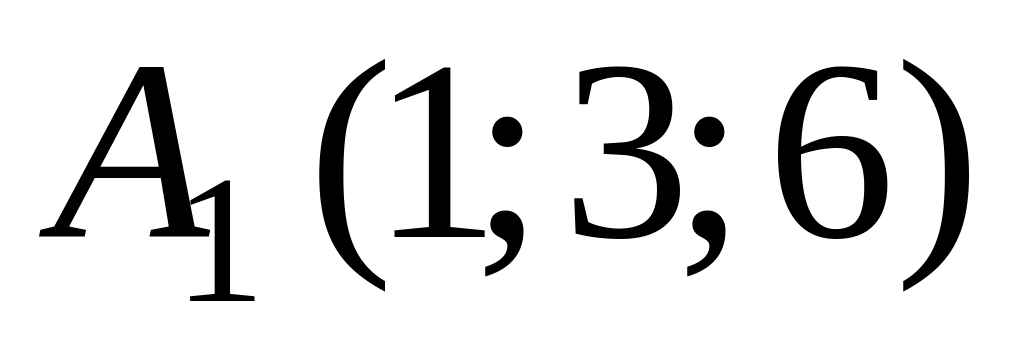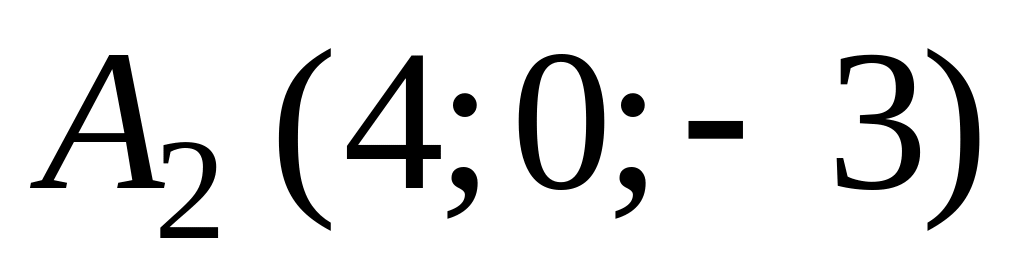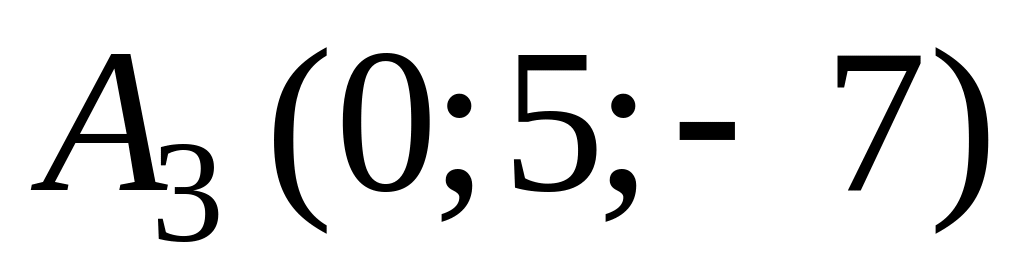4. Найти точки пересечения трех плоскостей, заданных в аффинной системе координат уравнениями , , .

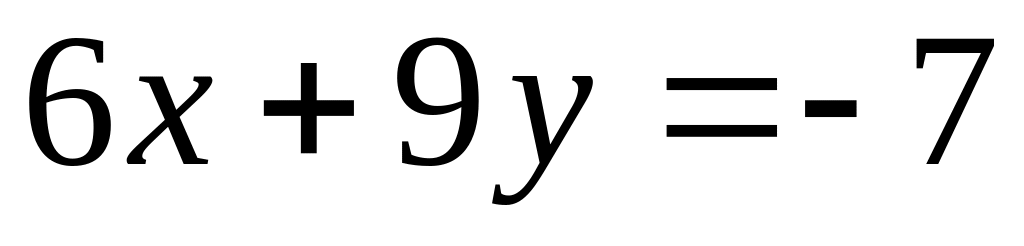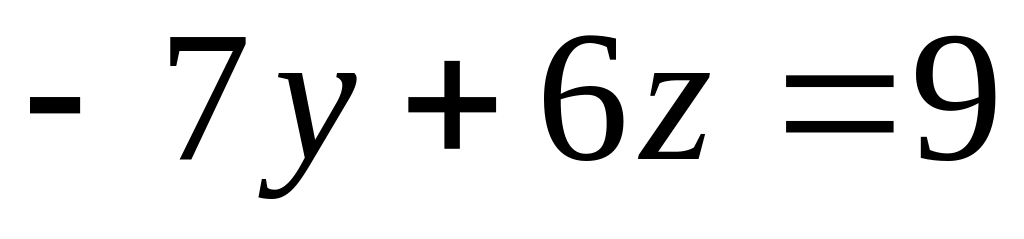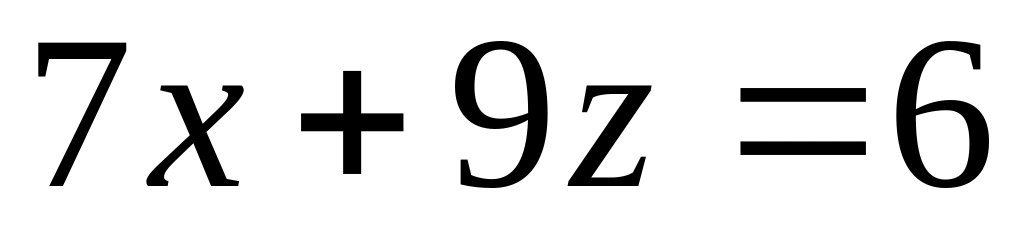5. В аффинной системе координат плоскости составить уравнения касательных к параболе 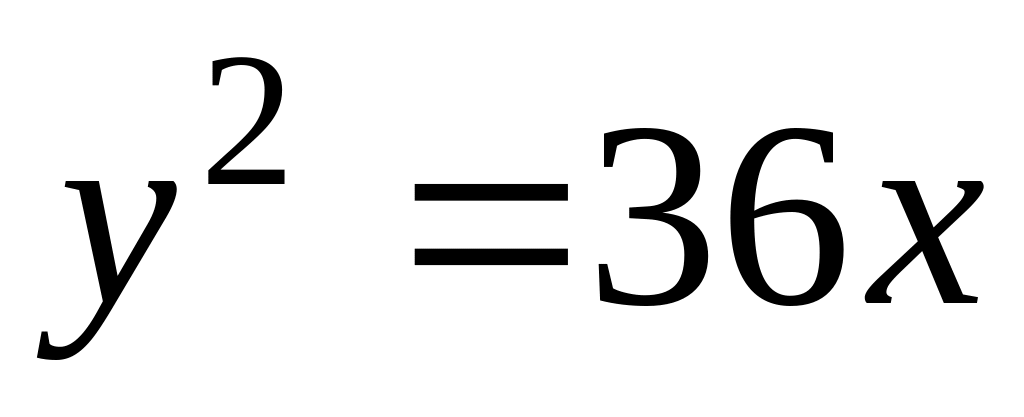, проведенных из точки .

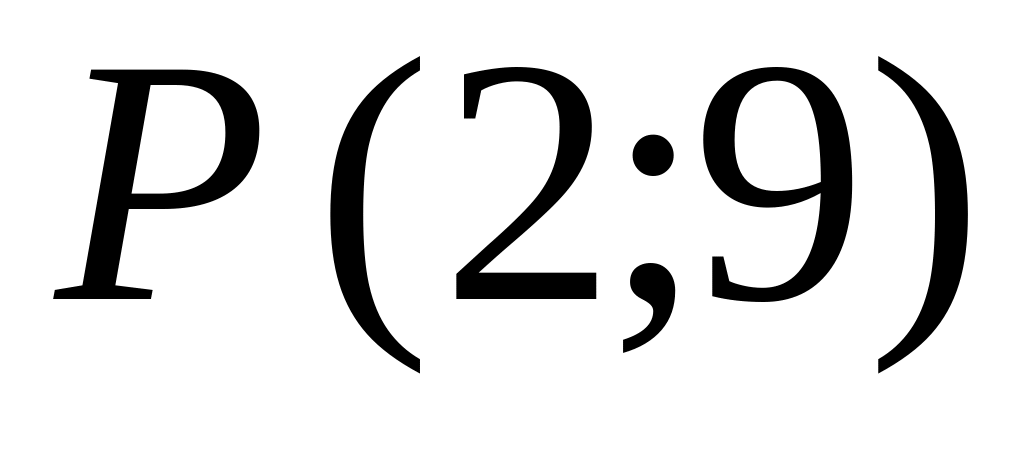Вариант 6

1. Общее уравнение плоскости.

2. Эллипс как сжатая окружность. Параметрические уравнения эллипса.

3. В аффинной системе координат пространства составить канонические и параметрические уравнения прямой, содержащей точки , .

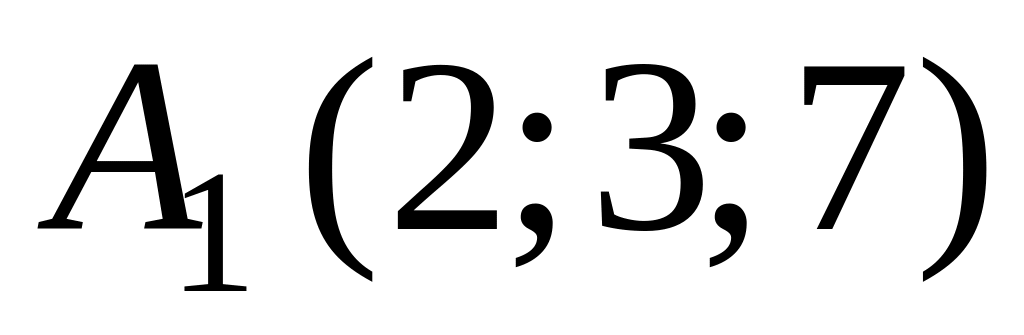4. Найти точки пересечения трех плоскостей, заданных в аффинной системе координат уравнениями , , .

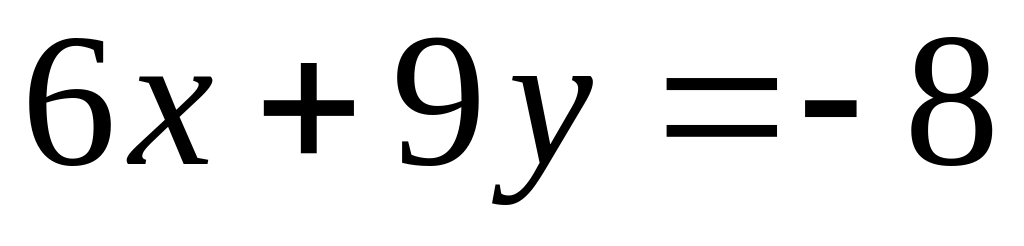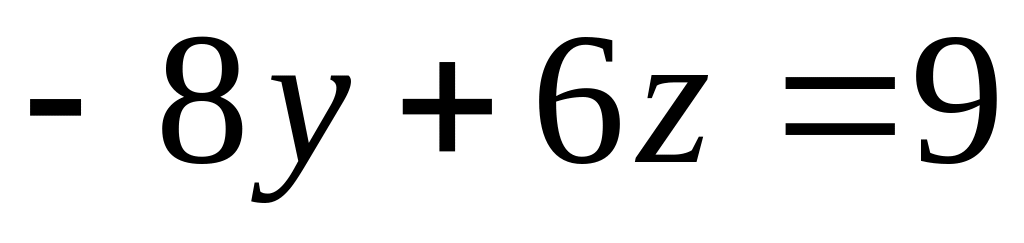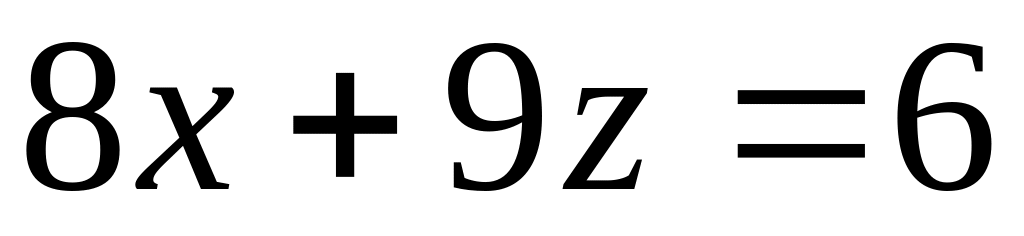5. В аффинной системе координат плоскости составить уравнения касательных к эллипсу 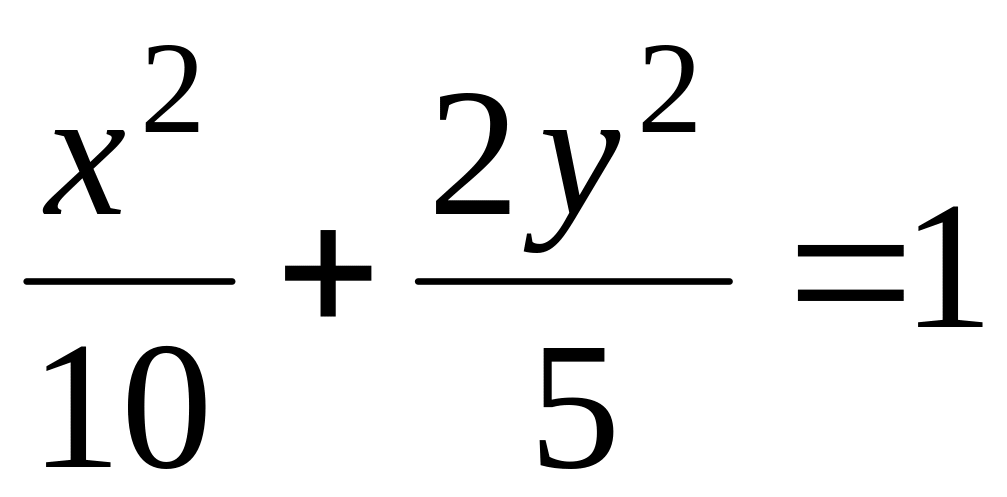, параллельных прямой .

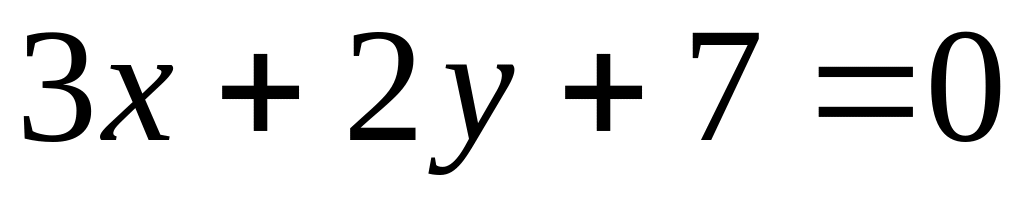Вариант 7

1. Расстояние от точки до плоскости.

2. Фокальное свойство гиперболы.

3. В аффинной_ системе координат пространства составить уравнение плоскости, проходящей через точку 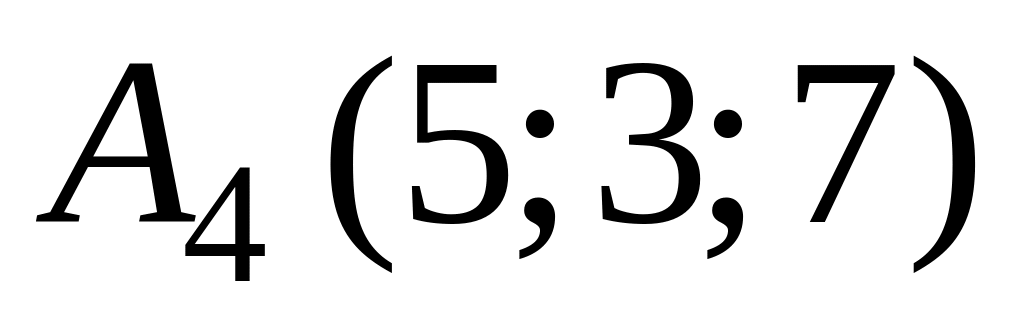и параллельной плоскости, содержащей точки , , , .

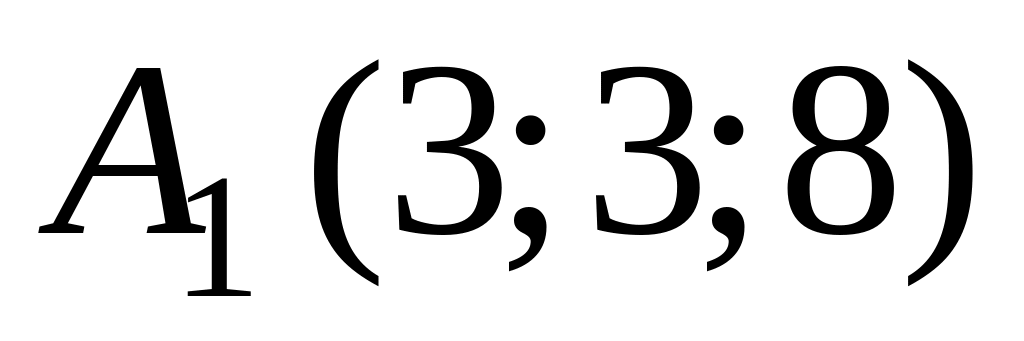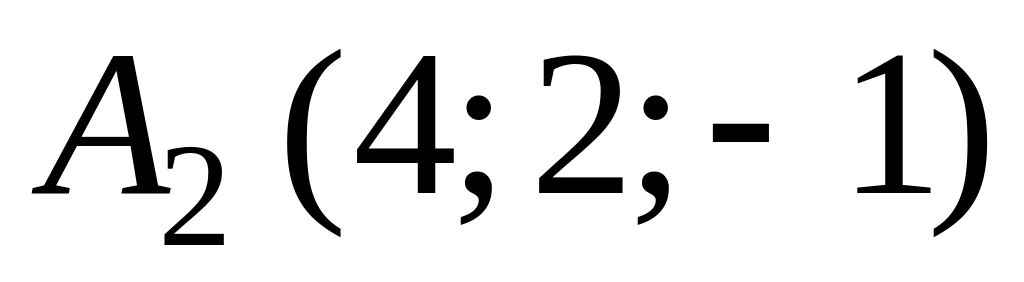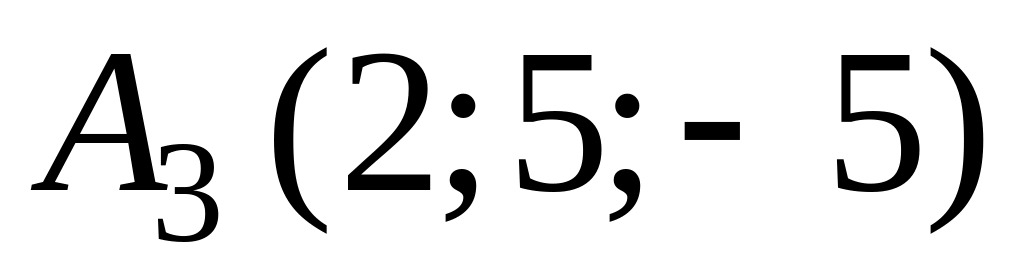4. Найти точки пересечения трех плоскостей, заданных в аффинной системе координат уравнениями , , .

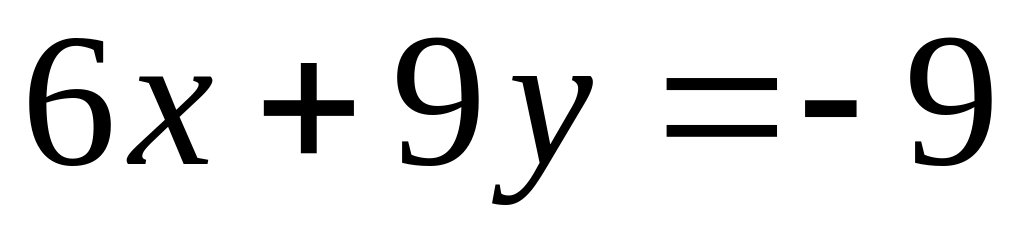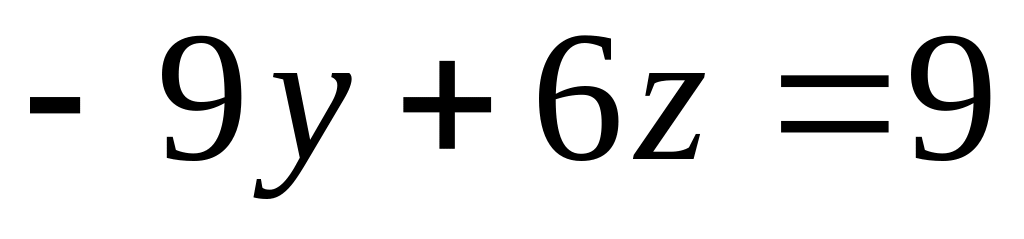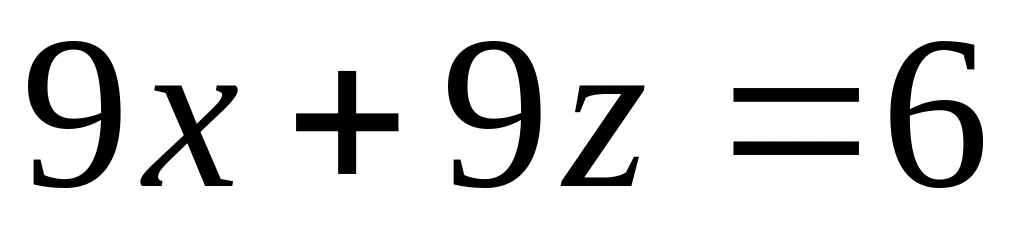5. В ортонормированной системе координат плоскости определить точки гиперболы 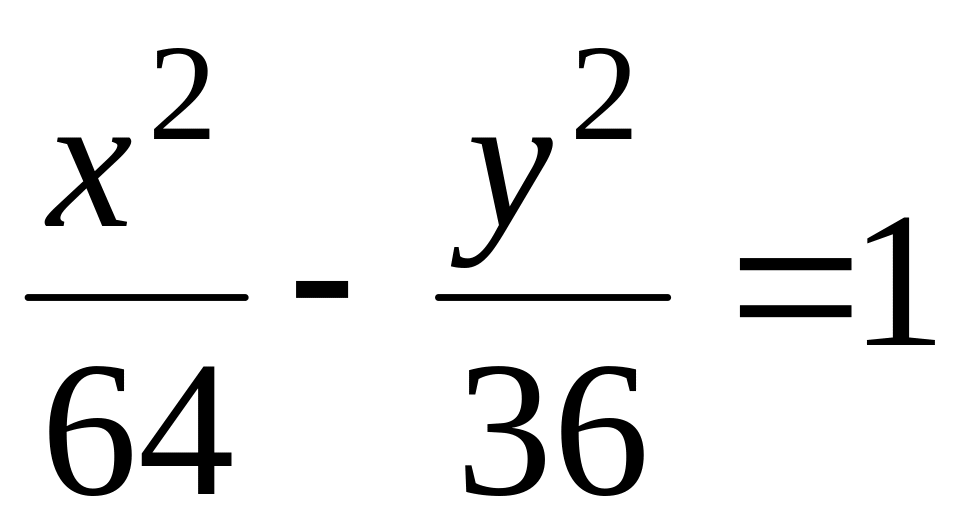, расстояния от которых до правого фокуса равно 4,5.

Вариант 8