21.Непрерывность функций в точке. Действия над непрерывными функциями.

Непрерывность функций. (в точке). Пусть функция у=f(x) определена в точке х0 и в некоторой окрестности этой точки. Функ-я у=f(x) наз-ся непрерывной в точке х0, сли сущест-т предел функции в этой точке и он равен знач-ю функ-и в этой точке, т.е. Limf(x)=f(x0) (х-->х0). Равенство означает выполнение 3х условий: 1)Функ-я f(x) определена в точке х0 и в её окрестн-ти

2)функ-я f(x) имеет предел при х->x0. 3)предел функ-и в точке х0 равен знач-ю функ-и в этой точке, т.е. выполняется равенство. Т.к. limf(x)=f(limx)=f(x0)

(под lim х->x0). Это означает, что при нахождении придела непрерывной функции f(x) можно перейти к приделу под знаком функции, т.е. в функцию f(x) вместо аргумента х подставить его предельное значение х0.

Св-ва: 1)f(x) и g(x) непрерыв. в т. х0, то их + и – также будут непрерывны. 2) функ. f(x) наз-ся непрерыв-ой на множ-ве, если она непрерывна в каждой т. этого множ-ва. 3)f(x) наз. огранич-ой сверху на множ-ве М, если сущ-т с=const такая что f(x)c, для всех хМ 4)f(x) наз-ся огранич-й снизу на множ-ве М, если сущ-т c=const, такая что f(x)-с. 5)f(x) наз-ся огран-ой на множ-ве М, если сущ-т c=const: |f(x)|<c 6)с-наз-ся верх. гран. F на множ-ве М, если f(x)c 7)c-ниж. гран. F на М, если f(x)c. 8)Если f не огр. сверху, то supf(x)=+  9)Если f не огр. снизу, то inff(x)=

22.Точка разрыва функций и их классификация.

Пусть функция y=f(x) определена в точке х₀ и в некоторой окрестности этой точки. Функция y=f(x) называется непрерывной в точке х₀, если существует предел функции в этой точке и он равен значению функции в этой точке:

Это означает:

- функция определена в точке х₀ и в ее окрестности;

- функция имеет предел при х→х₀

- предел функции в точке х₀ равен значению функции в этой точке, т.е. выполняется равенство.

Это означает, что при нахождении предела непрерывной функции f(x) можно перейти к пределу под знаком функции, то есть в функции f(x) вместо аргумента х подставить предельное значение х₀

Точки разрыва функции – это точки в которых нарушается непрерывность функции.

Точка разрыва х₀ называется точкой разрыва 1 рода функции y=f(x), если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы)

и

При этом, если:

- А₁=А₂ то точка х₀ называется точкой устранимого разрыва;

- А₁≠А₂ то точка х₀ называется точкой конечного разрыва.

|A₁ – A₂| называется скачком функции.

Точка разрыва х₀ называется точкой разрыва 2 рода функции y=f(x), если по крайней мере один из односторонних пределов (слева или справа) не существует, либо равен бесконечности.

23. Производная от функции. Её геометрический и механический смысл Связь между непрерывностью и дифференцируемостью функции.

Производной функции y=f(x) в точке х₀ называется предел отношения приращения функции к приращению аргумента, когда аргумент стремится к нулю.

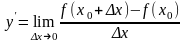
Производная функции f(x) есть некоторая функция

f ’(x), произведенная из данной функции.

Функция y=f(x), имеющая производную в каждой точке интервала (a;b) называется дифференцируемой в этом интервале.

Операция нахождения производной называется дифференцированием.

Дифференциал функции y=f(x) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dy (или df(x) ).

Иначе. Дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.

Геометрич-й смысл прпоиз-ой. Угловой коэф-т касательной k=tga=

=lim(дельтах->0)дельтау/дельтах. Это равенство перепишем в виде f’(x)=tga=k т.е. произ-ая f’(x) в точке х равна угловому коэф-ту касательной к графику у=f(x) в точке, абсцисса которой равна х.