1. Поняття симплекс методу. Запис математичної моделі симплекс методу

Симплекс-метод — метод розв'язання задачі лінійного програмування, в якому здійснюється скерований рух по опорних планах до знаходження оптимального розв'язку.

(2ой вопрос )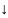

2.Загальний алгоритм рішення задачі симплекс методом, яка умова повинна виконуватись, для висновку про оптимальність рішення.

Для рішення задачі відповідним методом необхідно привести її до канонічного вигляду.

Постановка задачі:

1.Необхідно знайти оптимальне рішення за умови виконання необхідних вимог

2.Збір, обробка інформації , де

-техніко-економічні коефіцієнти при невідомих

-коефіцієнт цільової функції

-обсяги обмежень

3.Необхідно знайти вектор F ( , що задовольняє критерію оптимальності

4.Запис математичної моделі

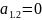
На основі одержаного завдання сформуємо вихідну симплекс-таблицю:

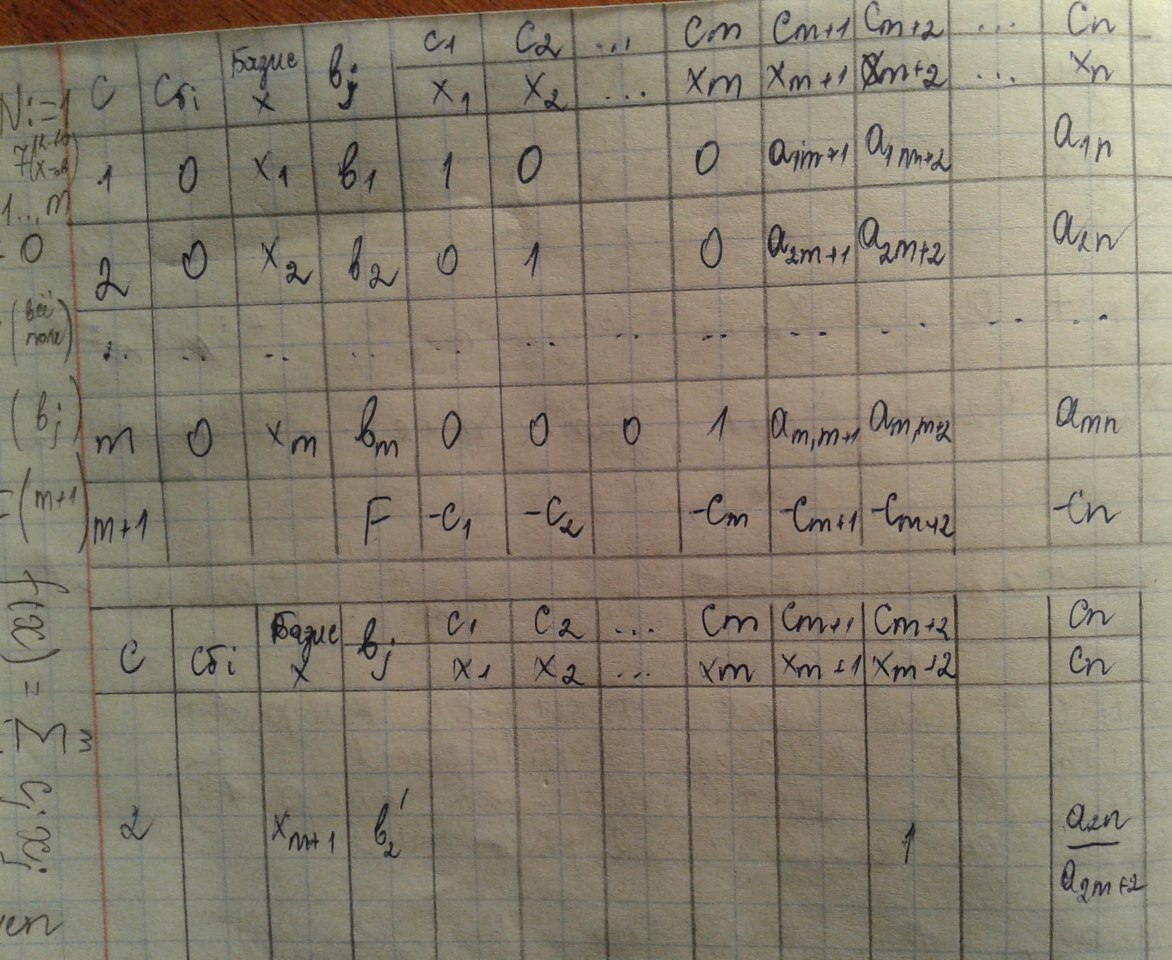
(после 1ой таблици)

5.Визначення ключового елементу:

5.1 Визначення ключового стовпця (коефіцієнт m+1 по модулю)

5.2 Визначення ключового рядка (обсяги обмежень поділити на відповідні елементи ключового стовпця, з відповідної частки вибираємо мінімальну)

На перетині ключового рядка і ключового стовпця знаходиться ключовий елемент.

6.Визначення елементів наступної таблиці

6.1Визначення початкового рядка наступної таблиці – відповідний елемент ключового рядка попер.табл.розділити на ключовий елемент попередньої таблиці.

6.2Визначення наступних елементів наступної таблиці. Від відповідного елементу попередньої таблиці відняти добуток відповідного елементу ключового стовпця попередньої таблиці та елементу початкового рядка наступної таблиці у відповідному стовпці.

Перевірка плану на оптимальність. Якщо знайдеться хоча б один коефіцієнт індексного рядка менше нуля, то план не оптимальний, і його необхідно поліпшити.

3. Перша симплексна таблиця для розв’язку задач лінійного програмування

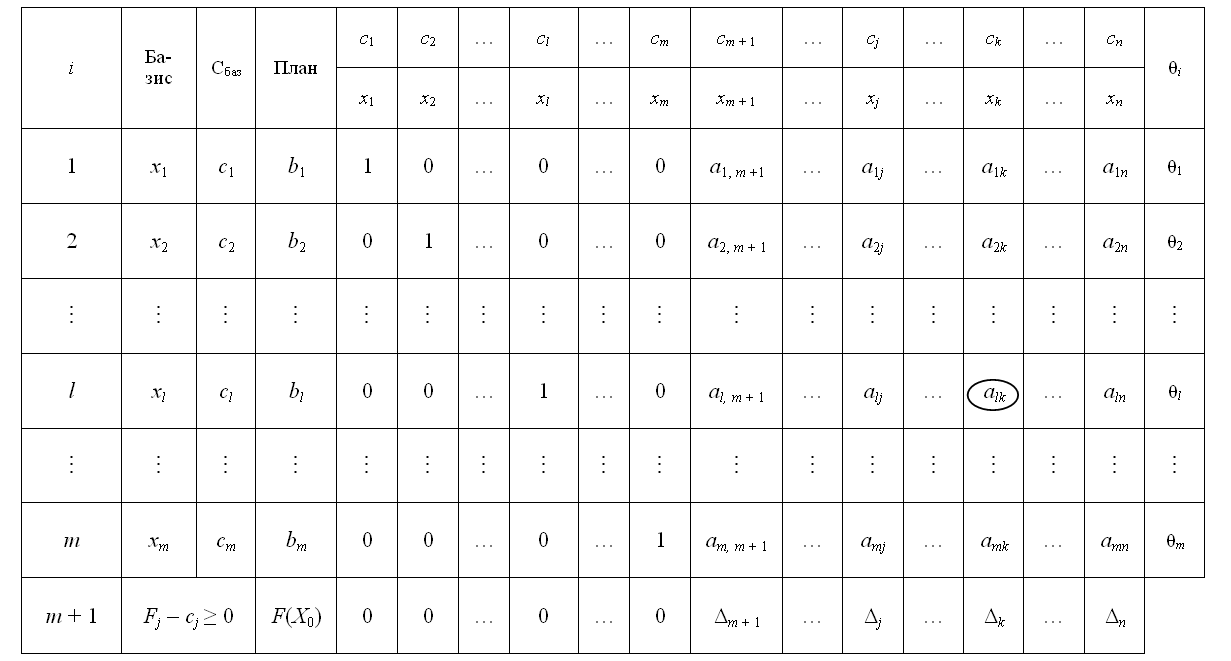Після заповнення табл.4.1 розраховують значення оцінок плану (останній рядок). Потім згідно з умовою оптимальності плану задачі лінійного програмування, якщо всі   (для задачі на максимум), то план є оптимальним. Допустимо, що одна з оцінок  , тоді план   не є оптимальним і необхідно здійснити перехід до наступного опорного плану, якому буде відповідати більше значення функціонала. Якщо від’ємних оцінок кілька, то включенню до базису підлягає вектор, який вибирається як  . Мінімум знаходять для тих індексів j, де  . Якщо існує кілька однакових значень оцінок, що відповідають  , то з відповідних їм векторів до базису включають той, якому відповідає максимальне значення функціонала.  Якщо хоча б для однієї від’ємної оцінки   всі коефіцієнти розкладу   відповідного вектора недодатні, то це означає, що функціонал є необмеженим на багатограннику розв’язків, тобто багатогранник у даному разі являє собою необмежену область і розв’язком задачі є  .

Розв’язання задачі лінійного програмування на відшукання мінімального значення функціонала відрізняється лише умовою оптимальності опорного плану. До базису включають вектор, для якого  , де максимум знаходять для тих j, яким відповідають  . Всі інші процедури симплексного методу здійснюються аналогічно, як у задачі лінійного програмування на відшукання максимального значення функціонала.