Вариант 23

1. Взаимное расположение прямих в пространстве Взаимное расположение двух прямых и пространстве характеризуется следующими тремя возможностями: 1)прямые лежат в одной плоскости и не имеют общих точек — параллельные прямые. 2)прямые лежат и одной плоскости и имеют одну общую точку — прямые пересекаются. 3)пространстве две прямые могут быть расположены еще так, что не лежат ни в одной плоскости. Такие прямые называются скрещивающимися (не пересекаются и не параллельны). Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая пересекает эту плоскость и точке, которая не лежит на первой прямой, то эти прямые скрещиваются. Теорема. Через каждую из двух скрещивающихся прямых проходит только одна плоскость, параллельная другой прямой. Примеры скрещивающихся прямых: трамвайный рельс и троллейбусный провод по пересекающейся улице, нeпересекающиеся и непараллельные ребра пирамид или призм и пр. Все три случая можно видеть еще на примере прямых, по которым встречаются стены и потолок или стены и пол комнаты.

2.Ортогональные инварианты уравнения кривой 2-го порядка.

Вариант 1 1. Ортогональное преобразование координат на пл-сти. См 1 Вариант 10 2. Оптическое св-во эллипса См 2 Вариант 28 Вариант 2 1. Пучок плоскостей Множество всех плоскостей, проходящих через одну и ту же прямую KM, называется пучком плоскостей.   Прямая KM называется осью пучка.

 Если известны уравнения двух различных плоскостей P₁ и P₂ 

  A₁x+B₁y+C₁z+D₁=0  

  А₂х+В₂у+C₂z+D₂=0  

принадлежащих пучку, то каждую плоскость пучка можно представить уравнением вида:

   m₁*(A₁x+B₁y+C₁z+D₁)+m₂*(А₂х+В₂у+C₂z+D₂)=0

  Это уравнение называется уравнением пучка плоскостей

  При P₁=0 получаем плоскость P₂ , а при P₂= 0 - плоскость P₁.  

  Когда m1≠0, мы можем разделить уравнение на m1. Обозначив m1:m1 через λ, получим уравнение:

     A₁x+B₁y+C₁z+D₁ +λ*( А₂х+В₂у+C₂z+D₂)=0 

2.Гиперболический параболоид

Вариант 3

1.Эллипс и его канонич. ур-е. См 2 Вариант 6 2.Прямая как пересечение двух плоскостей. См 1 Вариант 22

Вариант 3 1. Канонич и параметрич ур-я прямых. См 1 Вариант 22 2.Эллиптический параболоид

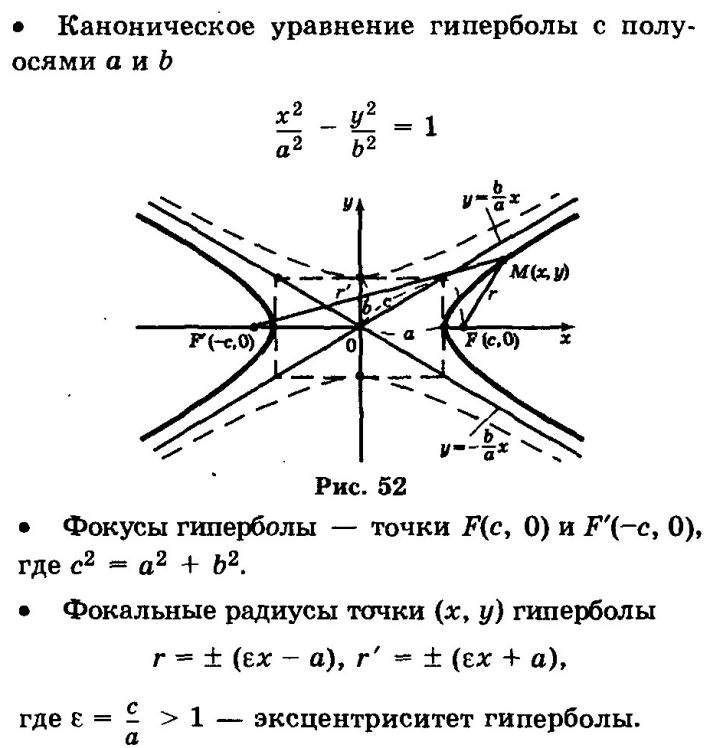
Вариант 4 1. Гипербола и ее канонич уравнение. Равнобочная гипербола Гипербола, асимптоты которой перпендикулярны, называется равнобочной.

2.Общее ур-е плоскости. См 1 Вариант 6

Вариант 5 1. Уравнение плоскости по точке параллельно двум векторам.

2.Ортогональные преобразования координат. См 1 Вариант 10

Вариант 7

1.Расстояние от точки до плоскости. Пусть плоскость   задана уравнением   и дана точка   . Тогда расстояние   от точки   до плоскости  определяется по формуле

 Доказательство.     Расстояние от точки   до плоскости   -- это, по определению, длина перпендикуляра   , опущенного из точки   на плоскость 

2. Фокальное свойство гиперболы: Гипербола является геометрическим местом точек,

разность расстояний от которых до фокусов по абсолютной величине постоянна:

|F1M − F2M| = 2a.

Вариант 8 1. Преобразование аффинных систем координат См 1 Вариант 29 2. Центры кривых второго порядка и центр симметрии. Центром кривой второго порядка называется ее центр симметрии. Кривая называется центральной, если она имеет единственный центр. Для таких кривых центр служит началом канонической системы координат. Координаты центра   определяются системой уравнений: