Вариант 6

1. Общее ур-е плоскости

2.Эллипс как сжатая окружность. Параметрические ур-я эллипса.

Эллипсом называется множество точек плоскости, для которых сумма расстояний до двух фиксированных точек F1 и F2 этой плоскости, называемых фокусами, есть величина постоянная. При совпадении точек F1 и F2 эллипс превращается в окружность. Эксцентриситетом эллипса называется величина е=с/а. Эллипс имеет две взаимно перпендикулярные оси симметрии (главные оси эллипса) и центр симметрии (центр эллипса). Если эллипс задан каноническим уравнением, то его главными осями являются оси координат, а центром – начало координат. Поскольку длины отрезков, образованных пересечением эллипса с главными осями, равны 2а и 2b (2a>2b), то главная ось, проходящая через фокусы, называется большой осью эллипса, а вторая главная ось – малой осью.

Вариант 22 1. Прямая как пересечение двух плоскостей

2.Упрощение ур-я центральной кривой 2-го порядка с помощью ортог. преобразований координат.

Вариант 21

1. Каноническое и параметрическое ур-е прямой

2.Полярное ур-е эллипса, гиперболы, параболы Полярное уравнение, общее по форме для эллипса, одной ветви гиперболы и параболы, имеет вид ,

где  ,   - полярные координаты произвольной точки линии, р - фокальный параметр (половина фокальной хорды линии, перпендикулярной к ее оси),   - эксцентриситет (в случае параболы  ). Полярная система координат при этом выбрана так, что полюс находится в фокусе, а полярная ось направлена по оси линии в сторону, противоположную ближайшей к этому фокусу директрисы.

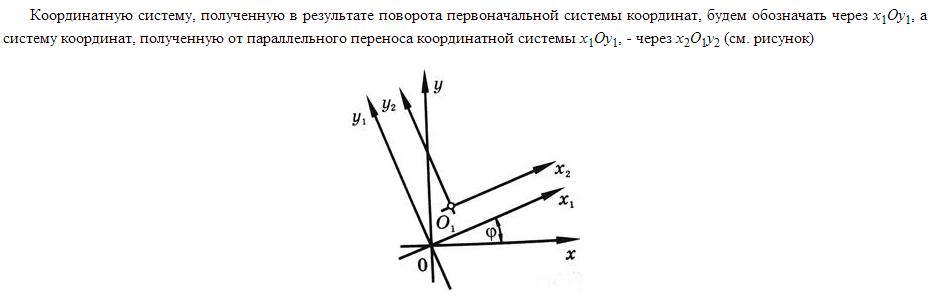
Вариант 29 1.Преобразования аффинных систем координат Рассмотрим ряд преобразований, связанных с переходом из одной системы координат в другую. Здесь ( х,  у ) и ( х',  у' ) - координаты произвольной точки Р соответственно в старой и новой системе координат.

 Параллельный перенос. Передвинем систему координат XОY в плоскости так, чтобы оси OX и OY оставались параллельны самим себе, а начало координат О сместилось в точку О' ( a, b ). Получим новую систему координат X'O'Y' . Координаты точки  Р  в новой и старой системе координат связаны соотношениями:

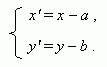
Поворот вокруг начала координат. Повернём систему координат XОY в плоскости на угол . Теперь координаты точки  Р  в новой и старой системе координат связаны соотношениями:

В частном случае    =    получим центральную симметрию относительно начала координат О :

  Гомотетия с центром  О ( a , b )  и коэффициентом  k   0 :

 

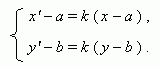
Аффинное преобразование:

 

 

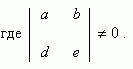
Аффинное преобразование переводит прямые в прямые, пересекающиеся прямые – в пересекающиеся прямые, параллельные прямые – в параллельные прямые. Все вышеприведенные преобразования координат являются аффинными.

 

2.Упрощение уравнения кривой параболического типа…

Вариант 24 1. Взаимное расположение прямой и плоскости. Известны три варианта взаимного расположения прямой и плоскости: 1)Прямая принадлежит плоскости 2)Прямая параллельна плоскости 3)Прямая пересекает плоскость. Теорема. Если прямая b параллельна хотя бы одной прямой а, принадлежащей плоскости  , то прямая параллельна плоскости  .

Предположим, что прямая m пересекает плоскость   в точке Q.Если m перпендикулярна каждой прямой плоскости  , проходящей через точку Q, то прямая m называется перпендикулярной к плоскости  .

Трамвайные рельсы иллюстрируют принадлежность прямых плоскости земли. Линии электропередачи параллельны плоскости земли, а стволы деревьев могут служить примерами прямых, пересекающих поверхность земли, некоторые перпендикулярные плоскости земли, другие — не перпендикулярные (наклонные).