
- •2.Геометрия, силы в зацеплении и расчет конических передач.
- •15. Геометрия, силы в зацеплении, к.П.Д. И кинематика червячных передач.
- •2.Диаграмма растяжения: характеристика зон. Основные механические характеристики материалов.
- •3.Дифференциальные зависимости при изгибе и проверка эпюр.
- •4.Диаграмма предельных напряжений. Определение коэффициента запаса при расчете на переменные напряжения.
- •1.Зубчатые передачи и их классификация. Геометрия эвольвентного зацепления.
- •1.2 Эвольвентное зацепление
- •2.Задачи кинематического анализа механизмов. Построение плана скоростей.
- •4.Исследование плоского напряженного состояния.
- •Выбор материала и допускаемых напряжений
- •Допускаемые изгибные напряжения
- •2.Классификация и обозначения подшипников качения. Расчет динамической грузоподъемности.
- •3.Кинематические пары и их классификация. Кинематические цепи и степень подвижности.
- •4.Напряженное состояние в точке и его виды. Методика исследования напряженного состояния.
- •1.Обобщенный закон Гука.
- •2.Определение касательных напряжений при изгибе (формула Журавского). Потенциальная энергия деформации.
- •6.Определение напряжений при чистом сдвиге. Условие прочности. Расчет заклепочных и сварных соединений.
- •7. Определение внутренних сил, напряжений и углов закручивания при кручении.
- •8.Определение положения главных осей и главных моментов инерции.
- •9.Определение главных напряжений и экстремальных касательных напряжений при объемном напряженном состоянии.
- •10.Общие сведения о ременных передачах. Силы и напряжения в ременной передаче. Давление на вал.
- •7. Понятие об устойчивости и критическая сила. Обобщенная формула Эйлера. Радиус инерции. Гибкость стержня.
- •8. Пределы применимости формулы Эйлера. Формула Ясинского. Проектный расчет методом последовательных приближений.
- •9. Порядок проектного расчета цилиндрических передач.
- •2. Определяют допускаемые напряжения
- •10. Порядок подбора подшипников качения.
- •12. Понятие об усталостной прочности. Характеристики цикла напряжений. Кривые усталости и предел выносливости.
- •1.2 Характеристики цикла напряжений
- •1. Расчет цилиндрических витых пружин.
- •2. Расчет цилиндрических зубчатых передач: определение сил в зацеплении, расчет по контактным напряжениям и напряжениям изгиба.
- •1.5 Расчет цилиндрических зубчатых передач
- •3. Расчет червячных передач по контактным напряжениям и напряжениям изгиба.
- •Где коэффициент нагрузки (9)
- •Допускаемые контактные напряжения - (12)
- •6. Расчет сварных соединений внахлестку. Выбор допускаемых напряжений.
- •7. Резьбовые соединения. Крепежные детали и виды резьб. Параметры метрической резьбы. Расчет резьбы.
- •9. Расчет стержня болта.
- •10. Расчет шпоночных и шлицевых соединений.
- •1.Структурная классификация плоских механизмов.
- •2. Статические моменты и центр тяжести.
- •2. Три основные задачи, решаемые из условия прочности.
- •3. Тяговый расчет ременной передачи, порядок проектного расчета.
- •2. Условие прочности и жесткости при кручении. Потенциальная энергия деформаций.
2.Диаграмма растяжения: характеристика зон. Основные механические характеристики материалов.
Опытным путем установлено, что для каждого материала существует характерные напряжения, при которых происходят качественные изменения в материале: переход от упругого в пластическое состояние, появление общей или местной текучести и т.д. Эти напряжения называются механическими характеристиками и определятся экспериментально, путем испытаний на растяжение стандартных образцов с записью диаграммы деформирования.

На рисунке 1 показана диаграмма растяжения малоуглеродистой стали.
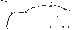
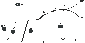
Рисунок 1.1 Диаграмма растяжения. Рисунок 1.2. Механические
лов
На этой диаграмме можно выделить четыре зоны: ОА – зона упругости; АВ – зона общей текучести; ВС – зона упрочнения; СД – зона местной текучести (разрушения).
Из
диаграммы можно определить механические
характеристики материалов, если ее
перестроить в координатах
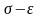 (рисунок 2). Различают следующие
механические характеристики:
(рисунок 2). Различают следующие
механические характеристики:
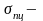 предел
пропорциональности - это наибольшее
напряжение, до которого материал
подчиняется закону Гука;
предел
пропорциональности - это наибольшее
напряжение, до которого материал
подчиняется закону Гука;
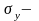 предел упругости
– это наибольшее напряжение, до которого
материал не получает остаточных
деформаций.
предел упругости
– это наибольшее напряжение, до которого
материал не получает остаточных
деформаций.
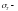 предел текучести-
это напряжение, при котором происходит
рост деформации без увеличения нагрузки;
предел текучести-
это напряжение, при котором происходит
рост деформации без увеличения нагрузки;
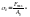 предел прочности.
предел прочности.
3.Дифференциальные зависимости при изгибе и проверка эпюр.
При изгибе справедливы следующие дифференциальные зависимости при изгибе.
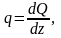
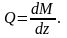
Эти выражения можно использовать для контроля полученных эпюр:
1. Если
брус загружен сосредоточенными силами
и моментами, то
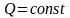 ,
эпюра
,
эпюра
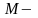 линейна (рисунок 1).
линейна (рисунок 1).
2. Если
брус загружен равномерно распределенной
нагрузкой, то эпюра
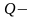 линейна,
парабола. (рисунок 2).
линейна,
парабола. (рисунок 2).
3. Если
на каком-то участке
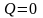 ,
то
,
то
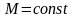 (чистый
изгиб).
(чистый
изгиб).
4. В той точке, где момент экстремален (рисунок 2).
5. В
сечениях приложения сосредоточенных
сил на эпюре
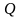 происходит скачок на величину приложенной
силы, а на эпюре М возникает излом.
происходит скачок на величину приложенной
силы, а на эпюре М возникает излом.
6. Скачок на эпюре моментов может быть только в том сечении, где приложен сосредоточенный момент. Величина скачка равна приложенному моменту.
4.Диаграмма предельных напряжений. Определение коэффициента запаса при расчете на переменные напряжения.
Диаграмма предельных напряжений
Если провести испытание стандартного образца из исследуемого материала в условиях несимметричного цикла напряжений, то получим диаграмму предельных напряжений, показанную на рисунке 3.
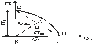
Рисунок 3. Диаграмма предельных напряжений.
Эта
диаграмма позволяет судить о близости
рабочих условий к предельным. Для этого
на диаграмму наносится рабочая точка
(В)с координатами
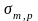 и
и
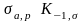 ,
где
и
,
где
и
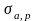 расчетные значения среднего и амплитудного
напряжения в детали. Здесь амплитуда
напряжения увеличена с учетом снижения
предела выносливости детали. По степени
близости рабочей точки к предельной
кривой судят об опасности рабочих
условий. Если рабочая точка окажется
за диаграммой, то непременно произойдет
усталостное разрушение.
расчетные значения среднего и амплитудного
напряжения в детали. Здесь амплитуда
напряжения увеличена с учетом снижения
предела выносливости детали. По степени
близости рабочей точки к предельной
кривой судят об опасности рабочих
условий. Если рабочая точка окажется
за диаграммой, то непременно произойдет
усталостное разрушение.
Построение этой диаграммы требует больших затрат времени и материальных ресурсов. Поэтому реальную диаграмму схематизируют прямой CD. Тогда эту диаграмму можно построить без проведения экспериментов.
Определение коэффициента запаса при переменных напряжениях
Коэффициент запаса очевидно равен отношению отрезка ОА к отрезку ОВ (рисунок 3). После геометрических построений получим:
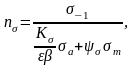
где
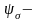 коэффициент чувствительности материала
к ассиметрии цикла.
коэффициент чувствительности материала
к ассиметрии цикла.
При действии переменных касательных напряжений
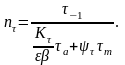
Коэффициенты
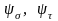 приводятся в справочниках.
приводятся в справочниках.
При одновременном действии переменных нормальных и касательных напряжений общий коэффициент запаса
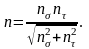
З
