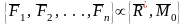- •2.Геометрия, силы в зацеплении и расчет конических передач.
- •15. Геометрия, силы в зацеплении, к.П.Д. И кинематика червячных передач.
- •2.Диаграмма растяжения: характеристика зон. Основные механические характеристики материалов.
- •3.Дифференциальные зависимости при изгибе и проверка эпюр.
- •4.Диаграмма предельных напряжений. Определение коэффициента запаса при расчете на переменные напряжения.
- •1.Зубчатые передачи и их классификация. Геометрия эвольвентного зацепления.
- •1.2 Эвольвентное зацепление
- •2.Задачи кинематического анализа механизмов. Построение плана скоростей.
- •4.Исследование плоского напряженного состояния.
- •Выбор материала и допускаемых напряжений
- •Допускаемые изгибные напряжения
- •2.Классификация и обозначения подшипников качения. Расчет динамической грузоподъемности.
- •3.Кинематические пары и их классификация. Кинематические цепи и степень подвижности.
- •4.Напряженное состояние в точке и его виды. Методика исследования напряженного состояния.
- •1.Обобщенный закон Гука.
- •2.Определение касательных напряжений при изгибе (формула Журавского). Потенциальная энергия деформации.
- •6.Определение напряжений при чистом сдвиге. Условие прочности. Расчет заклепочных и сварных соединений.
- •7. Определение внутренних сил, напряжений и углов закручивания при кручении.
- •8.Определение положения главных осей и главных моментов инерции.
- •9.Определение главных напряжений и экстремальных касательных напряжений при объемном напряженном состоянии.
- •10.Общие сведения о ременных передачах. Силы и напряжения в ременной передаче. Давление на вал.
- •7. Понятие об устойчивости и критическая сила. Обобщенная формула Эйлера. Радиус инерции. Гибкость стержня.
- •8. Пределы применимости формулы Эйлера. Формула Ясинского. Проектный расчет методом последовательных приближений.
- •9. Порядок проектного расчета цилиндрических передач.
- •2. Определяют допускаемые напряжения
- •10. Порядок подбора подшипников качения.
- •12. Понятие об усталостной прочности. Характеристики цикла напряжений. Кривые усталости и предел выносливости.
- •1.2 Характеристики цикла напряжений
- •1. Расчет цилиндрических витых пружин.
- •2. Расчет цилиндрических зубчатых передач: определение сил в зацеплении, расчет по контактным напряжениям и напряжениям изгиба.
- •1.5 Расчет цилиндрических зубчатых передач
- •3. Расчет червячных передач по контактным напряжениям и напряжениям изгиба.
- •Где коэффициент нагрузки (9)
- •Допускаемые контактные напряжения - (12)
- •6. Расчет сварных соединений внахлестку. Выбор допускаемых напряжений.
- •7. Резьбовые соединения. Крепежные детали и виды резьб. Параметры метрической резьбы. Расчет резьбы.
- •9. Расчет стержня болта.
- •10. Расчет шпоночных и шлицевых соединений.
- •1.Структурная классификация плоских механизмов.
- •2. Статические моменты и центр тяжести.
- •2. Три основные задачи, решаемые из условия прочности.
- •3. Тяговый расчет ременной передачи, порядок проектного расчета.
- •2. Условие прочности и жесткости при кручении. Потенциальная энергия деформаций.
2. Статические моменты и центр тяжести.
Статическими моментами называют следующие интегралы (рисунок 1):
Рисунок 1.
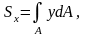
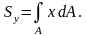
Пусть
известны статические моменты относительно
осей
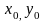 ,
параллельных осям
,
параллельных осям
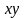 ,
но смещенных на расстояния
,
но смещенных на расстояния
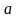 и
.
и
.
Найдем статические моменты относительно осей :
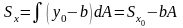 и
и
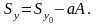
Расстояния
и
можно
подобрать так, чтобы было
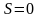 .
Ось, относительно которой статистический
момент равен нулю, называется центральной
осью.
Расстояние от произвольных осей
.
Ось, относительно которой статистический
момент равен нулю, называется центральной
осью.
Расстояние от произвольных осей
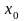 и
и
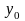 до центральных осей определяется по
формуле
до центральных осей определяется по
формуле
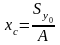 ,
,
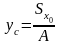 (1)
(1)
и называют координатами центра тяжести сечения. Отсюда следует, что статический момент относительно любой оси можно вычислить как произведение площади на расстояние от оси до центра тяжести сечения:
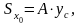
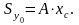 (2)
(2)
Если сечение имеет ось симметрии, то центр тяжести всегда лежит на этой оси. Для определения центра тяжести сложные сечения разбивают на простейшие фигуры.
3.Связи
и их реакции.
Материальные тела, ограничивающие
перемещение данного тела в пространстве,
называют связями.
Сила,
с которой связь действует на тело,
препятствуя его перемещениям, называется
силой
реакцией связи,
или просто реакцией
связи./
1. Гладкая
поверхность (плоскость). Реакция
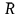 в случае гладкой поверхности направлена
по общей нормали к поверхностям связи
и тела в точке их контакта и приложена
к телу. 2. Подвижный
шарнир
(каток)
–
ограничивает движение тела в направлении
перпендикулярном плоскости опирания.
Поэтому реакция будет всегда направлена
перпендикулярно плоскости опирания.
3. Невесомый
стержень с шарнирами на концах. Реакция
прямолинейного невесомого стержня с
шарнирами на концах направлена вдоль
оси стержня. В отличие от нити такой
стержень может передавать как силы
растяжения, так и силы сжатия. Если
связью является криволинейный стержень,
то его реакция будет направлена по
прямой АВ,
соединяющий
шарниры А
и
В.
4.
Цилиндрический шарнир (подшипник).
Цилиндрический шарнир представляет
собой цилиндрическую втулку, в которой
находится ось вращения. Он не воспринимает
осевой силы, его реакция находится в
плоскости
Axy,
перпендикулярной оси шарнира. Реакция
в случае гладкой поверхности направлена
по общей нормали к поверхностям связи
и тела в точке их контакта и приложена
к телу. 2. Подвижный
шарнир
(каток)
–
ограничивает движение тела в направлении
перпендикулярном плоскости опирания.
Поэтому реакция будет всегда направлена
перпендикулярно плоскости опирания.
3. Невесомый
стержень с шарнирами на концах. Реакция
прямолинейного невесомого стержня с
шарнирами на концах направлена вдоль
оси стержня. В отличие от нити такой
стержень может передавать как силы
растяжения, так и силы сжатия. Если
связью является криволинейный стержень,
то его реакция будет направлена по
прямой АВ,
соединяющий
шарниры А
и
В.
4.
Цилиндрический шарнир (подшипник).
Цилиндрический шарнир представляет
собой цилиндрическую втулку, в которой
находится ось вращения. Он не воспринимает
осевой силы, его реакция находится в
плоскости
Axy,
перпендикулярной оси шарнира. Реакция
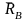 может быть направлена по любому радиусу
шарнира в плоскости Axy.
5.
Подпятник.
Он отличается от цилиндрического
шарнира тем, что кроме радиальных сил
может воспринимать и осевую силу.
Реакция подпятника, как и реакция
сферического шарнира, может иметь любое
направление в пространстве. 6. Гибкие
связи.
Этим термином обозначают цепи, тросы,
канаты, которые могут воспринимать
только силы растяжения. Их реакции
направлены вдоль этих связей.
7.
Сферический
шарнир.
Он позволяет телу поворачиваться, но
не разрешает линейные перемещения.
Реакция шарнира
может быть направлена по любому радиусу
шарнира в плоскости Axy.
5.
Подпятник.
Он отличается от цилиндрического
шарнира тем, что кроме радиальных сил
может воспринимать и осевую силу.
Реакция подпятника, как и реакция
сферического шарнира, может иметь любое
направление в пространстве. 6. Гибкие
связи.
Этим термином обозначают цепи, тросы,
канаты, которые могут воспринимать
только силы растяжения. Их реакции
направлены вдоль этих связей.
7.
Сферический
шарнир.
Он позволяет телу поворачиваться, но
не разрешает линейные перемещения.
Реакция шарнира
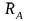 приложена к его центру и может быть
направлена по любому радиусу шарнира
приложена к его центру и может быть
направлена по любому радиусу шарнира
4.
Способы задания движения.
Закон движения может быть задан
естественным способом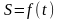 ,
координатным способом:
,
координатным способом:
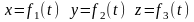 ;
и векторным способом:
;
и векторным способом:
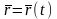 . /
Основная задача кинематики состоит в
том, чтобы, зная закон движения данного
тела (или точки) определить все
кинематические характеристики
(траектории, скорости, ускорения)
движения тела в целом и каждой его точки
в отдельности./ Естественным способом
задания движения удобно пользоваться
тогда, когда траектория движения S
известна заранее. При движении точки
по кривой полное ускорение точки удобно
раскладывать на две составляющие: по
касательной и нормали к траектории.
Касательное и нормальное ускорение
точки определяются выражениями
. /
Основная задача кинематики состоит в
том, чтобы, зная закон движения данного
тела (или точки) определить все
кинематические характеристики
(траектории, скорости, ускорения)
движения тела в целом и каждой его точки
в отдельности./ Естественным способом
задания движения удобно пользоваться
тогда, когда траектория движения S
известна заранее. При движении точки
по кривой полное ускорение точки удобно
раскладывать на две составляющие: по
касательной и нормали к траектории.
Касательное и нормальное ускорение
точки определяются выражениями
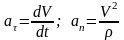 ,
где
- радиус кривизны траектории в
рассматриваемой точке./ Полная скорость
теперь будет равна
,
где
- радиус кривизны траектории в
рассматриваемой точке./ Полная скорость
теперь будет равна
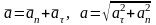 ./
При координатном способе задания
движения скорости и ускорения определяются
так
./
При координатном способе задания
движения скорости и ускорения определяются
так
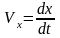 ,
,
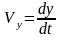 ,
,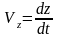 ;
;
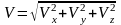 ;
;
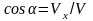 ;
;
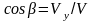 ;
;
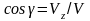 ;
;
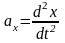 ;
;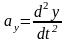 ;
;
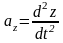 ;
;
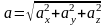 Направляющие косинусы определяются
аналогично./ При векторном способе
задания движения точки определяются
так:
Направляющие косинусы определяются
аналогично./ При векторном способе
задания движения точки определяются
так:
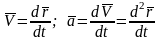 .
Вектор скорости всегда направлен по
касательной к траектории.
.
Вектор скорости всегда направлен по
касательной к траектории.
5.
Скорости и ускорения точек.
Теорема
о проекциях скоростей. Проекция
скоростей двух точек тела на прямую,
соединяющую эти точки, равны друг другу
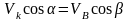 ./
Точка, скорость которой в данный момент
времени равна нулю, называется мгновенным
центром скоростей. Скорость любой точки
равна вращательной скорости вокруг
мгновенного центра скорости:
./
Точка, скорость которой в данный момент
времени равна нулю, называется мгновенным
центром скоростей. Скорость любой точки
равна вращательной скорости вокруг
мгновенного центра скорости:
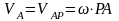 /
Скорости точек тела пропорциональны
их расстояниям до мгновенного центра
скорости
/
Скорости точек тела пропорциональны
их расстояниям до мгновенного центра
скорости
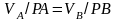 ./
Для определения мгновенного центра
скорости достаточно знать направления
скоростей каких-нибудь двух точек./
Теорема.
Ускорение любой точки тела геометрически
складывается из ускорения полюса и
ускорения этой точки относительно
полюса при вращательном движении:
./
Для определения мгновенного центра
скорости достаточно знать направления
скоростей каких-нибудь двух точек./
Теорема.
Ускорение любой точки тела геометрически
складывается из ускорения полюса и
ускорения этой точки относительно
полюса при вращательном движении:
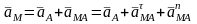 .
Если полюс движется не прямолинейно,
то
.
Если полюс движется не прямолинейно,
то
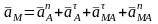 .
.
Т
1.Теоремы
статики: Вариньона, о переносе сил,
приведение сил к одному центру.
Теорема Вариньона: момент равнодействующей
плоской системы сходящихся сил
относительно любого центра равен
алгебраической сумме моментов слагаемых
сил относительно того же центра. Эта
теорема справедлива и для моментов
относительно любой оси
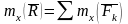 ./
Теорема о параллельном переносе в
другую точку тела (лемма статики). Силу,
приложенную к твердому телу, можно, не
изменяя ее действия, перенести параллельно
самой себе в любую точку тела, прибавляя
при этом пару с моментом, равным моменту
переносимой силы относительно точки,
в которую она переносится./ Точку,
к которой приводят систему сил, называют
центром
приведения
данной системы сил./
Теорема.
Произвольную систему сил, действующих
на твердое тело, можно привести к
какому-либо центру, заменив все
действующие силы одной силой, равной
главному вектору системы сил, приложенному
в этом центре, и одной парой сил с
моментом, равным главному моменту
системы сил относительно того же центра
(теорема Пуансо).
./
Теорема о параллельном переносе в
другую точку тела (лемма статики). Силу,
приложенную к твердому телу, можно, не
изменяя ее действия, перенести параллельно
самой себе в любую точку тела, прибавляя
при этом пару с моментом, равным моменту
переносимой силы относительно точки,
в которую она переносится./ Точку,
к которой приводят систему сил, называют
центром
приведения
данной системы сил./
Теорема.
Произвольную систему сил, действующих
на твердое тело, можно привести к
какому-либо центру, заменив все
действующие силы одной силой, равной
главному вектору системы сил, приложенному
в этом центре, и одной парой сил с
моментом, равным главному моменту
системы сил относительно того же центра
(теорема Пуансо).