
- •2.Геометрия, силы в зацеплении и расчет конических передач.
- •15. Геометрия, силы в зацеплении, к.П.Д. И кинематика червячных передач.
- •2.Диаграмма растяжения: характеристика зон. Основные механические характеристики материалов.
- •3.Дифференциальные зависимости при изгибе и проверка эпюр.
- •4.Диаграмма предельных напряжений. Определение коэффициента запаса при расчете на переменные напряжения.
- •1.Зубчатые передачи и их классификация. Геометрия эвольвентного зацепления.
- •1.2 Эвольвентное зацепление
- •2.Задачи кинематического анализа механизмов. Построение плана скоростей.
- •4.Исследование плоского напряженного состояния.
- •Выбор материала и допускаемых напряжений
- •Допускаемые изгибные напряжения
- •2.Классификация и обозначения подшипников качения. Расчет динамической грузоподъемности.
- •3.Кинематические пары и их классификация. Кинематические цепи и степень подвижности.
- •4.Напряженное состояние в точке и его виды. Методика исследования напряженного состояния.
- •1.Обобщенный закон Гука.
- •2.Определение касательных напряжений при изгибе (формула Журавского). Потенциальная энергия деформации.
- •6.Определение напряжений при чистом сдвиге. Условие прочности. Расчет заклепочных и сварных соединений.
- •7. Определение внутренних сил, напряжений и углов закручивания при кручении.
- •8.Определение положения главных осей и главных моментов инерции.
- •9.Определение главных напряжений и экстремальных касательных напряжений при объемном напряженном состоянии.
- •10.Общие сведения о ременных передачах. Силы и напряжения в ременной передаче. Давление на вал.
- •7. Понятие об устойчивости и критическая сила. Обобщенная формула Эйлера. Радиус инерции. Гибкость стержня.
- •8. Пределы применимости формулы Эйлера. Формула Ясинского. Проектный расчет методом последовательных приближений.
- •9. Порядок проектного расчета цилиндрических передач.
- •2. Определяют допускаемые напряжения
- •10. Порядок подбора подшипников качения.
- •12. Понятие об усталостной прочности. Характеристики цикла напряжений. Кривые усталости и предел выносливости.
- •1.2 Характеристики цикла напряжений
- •1. Расчет цилиндрических витых пружин.
- •2. Расчет цилиндрических зубчатых передач: определение сил в зацеплении, расчет по контактным напряжениям и напряжениям изгиба.
- •1.5 Расчет цилиндрических зубчатых передач
- •3. Расчет червячных передач по контактным напряжениям и напряжениям изгиба.
- •Где коэффициент нагрузки (9)
- •Допускаемые контактные напряжения - (12)
- •6. Расчет сварных соединений внахлестку. Выбор допускаемых напряжений.
- •7. Резьбовые соединения. Крепежные детали и виды резьб. Параметры метрической резьбы. Расчет резьбы.
- •9. Расчет стержня болта.
- •10. Расчет шпоночных и шлицевых соединений.
- •1.Структурная классификация плоских механизмов.
- •2. Статические моменты и центр тяжести.
- •2. Три основные задачи, решаемые из условия прочности.
- •3. Тяговый расчет ременной передачи, порядок проектного расчета.
- •2. Условие прочности и жесткости при кручении. Потенциальная энергия деформаций.
3. Расчет червячных передач по контактным напряжениям и напряжениям изгиба.
Проверенный расчет по контактным напряжениям проводится по формуле
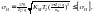
Где коэффициент нагрузки (9)
Коэффициент
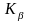 учитывает неравномерность нагрузки
по длине контактной линии:
учитывает неравномерность нагрузки
по длине контактной линии:
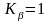 - для постоянной нагрузки и
- для постоянной нагрузки и
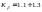 - для переменной нагрузки. Коэффициент
динамичности
- для переменной нагрузки. Коэффициент
динамичности
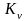 берется из таблиц в зависимости от
скорости скольжения и степени точности.
берется из таблиц в зависимости от
скорости скольжения и степени точности.
Проектный расчет по контактным напряжениям производится по формуле, полупрямой из (8):
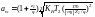 . (10)
. (10)
Проверку по напряжениям изгиба проводят по формуле:
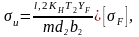 (11)
(11)
где
коэффициент формы зуба
берется из таблиц в зависимости от
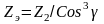 .
.
Тело червяка рассчитывается как вал на изгиб с кручением (см. тему 11).
Материалы и допускаемые напряжения
Червяки изготавливают из среднеуглеродистых и легированных сталей (40Х, 40ХН, 35ХГСА) с поверхностной или объемной закалкой до HRC 45-55 или цементируемых сталей (15Х, 20Х, 12ХНЗА) с последующей закалкой до HRC 56-62. Термообработанные червяки шлифуются. Для тихоходных передач могут применяться нешлифованные червяки с НВ 280-300. Материал червячных колес выбирают с учетом скорости скольжения, он должен обладать хорошими антишлифовочными свойствами. Лучшими антишлифовочными свойствами обладают оловянно-фосфоритные бронзы (Бр 0101щ).
Часто применяют оловянно-цинково-свинцовые бронзы (Бр 05 Ц5 C5). Они дороги и их применяют при Vs=625м/с.
При Vs=26м/с применяют менее дорогие алюминиевые бронзы (Бр А9 Ж3 Л). При этом из бронзы изготавливают венец, а колесный центр делают из чугуна.
При Vs 2м/с колеса изготавливаются из серого чугуна С4-15-32.
Допускаемые напряжения определяют умножением табличных значений на коэффициенты долговечности:
Допускаемые контактные напряжения - (12)
допускаемые изгибные напряжения при симметричном цикле (реверсивные передачи) –
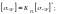 (13)
(13)
допускаемые изгибные напряжения при пульсирующем цикле (нереверсивные передачи)-
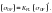
Штрихами обозначены их табличные величины, выбираемые в зависимости от материала и способа литья.
Коэффициент
долговечности: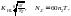
где
n
в об/мин, Т - срок службы в часах. Для
реверсивных передач
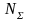 уменьшить вдвое. Должно быть
уменьшить вдвое. Должно быть
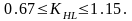 Если он окажется за указанными пределами,
то принять соответствующие предельные
значения.
Если он окажется за указанными пределами,
то принять соответствующие предельные
значения.
Коэффициент:
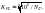 Должно быть:
Должно быть:
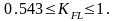
4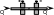 .
Растяжение – сжатие. Определение
продольных сил и напряжений в поперечных
и наклонных сечениях. Закон Гука.
Растяжение-сжатие
– это такой вид нагружения, когда в
поперечном сечении возникают только
продольные силы
.
Это возможно тогда, когда все внешние
силы действуют вдоль оси бруса.
Определение
напряжений и деформации.
Согласно методу сечений продольная
сила равна сумме проекций на ось бруса
всех внешних сил, действующих на
отсеченную (рассматриваемую) часть
бруса:
.
Растяжение – сжатие. Определение
продольных сил и напряжений в поперечных
и наклонных сечениях. Закон Гука.
Растяжение-сжатие
– это такой вид нагружения, когда в
поперечном сечении возникают только
продольные силы
.
Это возможно тогда, когда все внешние
силы действуют вдоль оси бруса.
Определение
напряжений и деформации.
Согласно методу сечений продольная
сила равна сумме проекций на ось бруса
всех внешних сил, действующих на
отсеченную (рассматриваемую) часть
бруса:
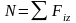 . При этом
рекомендуется направлять на растяжение./
Часто бывает полезным строить графики
изменения внутренних сил и перемещений
вдоль оси бруса. Эти графики называются
эпюрами. Эпюры продольных сил. / В
поперечном сечении бруса возникают
нормальные напряжения.
. При этом
рекомендуется направлять на растяжение./
Часто бывает полезным строить графики
изменения внутренних сил и перемещений
вдоль оси бруса. Эти графики называются
эпюрами. Эпюры продольных сил. / В
поперечном сечении бруса возникают
нормальные напряжения.
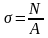 , где
, где
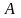 - площадь сечения./ Относительная
продольная деформация равна среднему
значению
- площадь сечения./ Относительная
продольная деформация равна среднему
значению
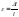 , где
- длина бруса (участка);
- абсолютное удлинение./ В пределах
малых деформаций для всех материалов
справедлив закон Гука:
, где
- длина бруса (участка);
- абсолютное удлинение./ В пределах
малых деформаций для всех материалов
справедлив закон Гука:
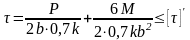 ,
где
,
где
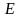 - модуль упругости материала, определяемый
экспериментально. Абсолютное удлинение
,
где
- модуль упругости материала, определяемый
экспериментально. Абсолютное удлинение
,
где
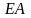 - жесткость бруса при растяжении-сжатии./
При расчетах брус разбивают на участки,
границами которых являются: - сечения,
где приложены силы, - сечения, где
меняется площадь, - сечения, где меняется
материал./ Если брус состоит из нескольких
участков, то общее удлинение находится
суммированием по участкам. Эпюра осевых
перемещений./ Если кроме нагрузок
действует температура, то общее удлинение
по принципу наложения равно
- жесткость бруса при растяжении-сжатии./
При расчетах брус разбивают на участки,
границами которых являются: - сечения,
где приложены силы, - сечения, где
меняется площадь, - сечения, где меняется
материал./ Если брус состоит из нескольких
участков, то общее удлинение находится
суммированием по участкам. Эпюра осевых
перемещений./ Если кроме нагрузок
действует температура, то общее удлинение
по принципу наложения равно
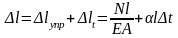 ,
где
- коэффициент теплового расширения
тела (для стали
,
где
- коэффициент теплового расширения
тела (для стали
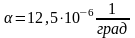 );
);
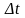 -
изменение температуры.
-
изменение температуры.
5. Расчет валов на изгиб с кручением.
Методика расчета валов
При расчете валов на изгиб и кручение по гипотезам прочности мы будем учитывать только крутящий и изгибающие моменты, действующие в опасном поперечном сечении, и не будем принимать во внимание поперечные силы, так как соответствующие им касательные напряжения относительно невелики.
Максимальные нормальные () и касательные () напряжения у круглых валов вычисляют по формулам:
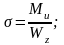
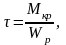
причем
для круглых валов выполняется
условие: 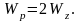 (2)
(2)
При сочетании изгиба и кручения опасными будут точки поперечного сечения вала, наиболее удаленные от нейтральной оси.
Применив III гипотезу прочности, получим
. (3)
Выражение, стоящее в числителе, назовем эквивалентным моментом
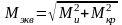 ,
,
тогда расчетная формула для круглых валов принимает вид
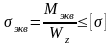 .
.
По этой формуле расчет валов ведут, как на изгиб, но не по изгибающему, а по эквивалентному моменту.
Применив V гипотезу прочности, получим
, (6)
тогда по энергетической теории прочности
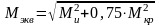 .
.
Выполненный проектный расчет вала по гипотезам прочности проверяется расчетом на прочность при напряжениях, переменных во времени - динамических нагрузках.
В проектном расчете не учитывалось то, что напряжения в сечениях вала изменяются во времени по циклическому закону, поперечные сечения вала имеют очаги концентрации напряжений (шпоночные канавки), а так же не учитывался масштабный фактор, качество поверхности и пр.
Проверочный расчет выполняется для определения коэффициента запаса прочности с учетом всех факторов риска и сравнения найденного значения с принятым нормативным значением.
Условие прочности имеет вид
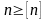 ,
,
где [п] – нормальный коэффициент запаса прочности;
п – фактический коэффициент запаса прочности данной детали при данном цикле напряжений.
При сложном напряженном состоянии общий коэффициент запаса прочности определяют по эмпирической формуле:
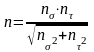
где nσ - коэффициент запаса прочности по нормальным напряжениям определяется по формулам:
при
симметричном цикле напряжений
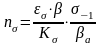 ;
;
при
асимметричном цикле напряжений
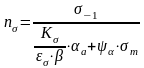 . (11)
. (11)
В приведенных формулах коэффициента запаса прочности:
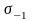 – предел выносливости
стандартного лабораторного образца
при изгибе или растяжении-сжатии при
симметричном цикле напряжений;
– предел выносливости
стандартного лабораторного образца
при изгибе или растяжении-сжатии при
симметричном цикле напряжений;
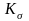 – эффективный
коэффициент концентрации напряжений;
– эффективный
коэффициент концентрации напряжений;
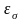 –
масштабный
фактор;
–
масштабный
фактор;
β – коэффициент качества поверхности;
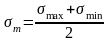 – среднее напряжение
цикла;
– среднее напряжение
цикла;
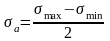 – амплитуда цикла
напряжения;
– амплитуда цикла
напряжения;
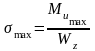 –
максимальное
нормальное напряжение цикла;
–
максимальное
нормальное напряжение цикла;
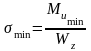 – минимальное
нормальное напряжение цикла;
– минимальное
нормальное напряжение цикла;
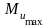 – максимальный
изгибающий момент;
– максимальный
изгибающий момент;
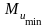 – минимальный
изгибающий момент;
– минимальный
изгибающий момент;
Wz = 0,1 d3 – осевой момент сопротивления вала;
d – диаметр поперечного сечения вала;
Ψσ
–
коэффициент, учитывающий влияние
асимметрии цикла на предел выносливости,
который при
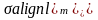 <
0 принимает нулевое значение (Ψσ
= 0).
<
0 принимает нулевое значение (Ψσ
= 0).
Напряжения
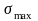 ;
;
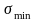 ;
;
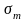 могут быть положительными, отрицательными
и равными нулю. Амплитуда
могут быть положительными, отрицательными
и равными нулю. Амплитуда
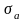 всегда
положительна.
всегда
положительна.
Безразмерная величина называется коэффициентом асимметрии цикла.
