7. Понятие об устойчивости и критическая сила. Обобщенная формула Эйлера. Радиус инерции. Гибкость стержня.

Понятие об устойчивости

Известно, что равновесие АТТ может быть устойчивым, неустойчивым и безразличным. Пример: равновесие шарика на гладкой вогнутой, выпуклой поверхности и на плоскости. Аналогичные явления наблюдаются и для деформируемых тонкостенных конструкций. Пример с сжатой линейкой: если сила меньше некоторого критического значения, линейка устойчива, 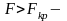неустойчива, 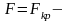безразличное равновесие.

Критическая сила – это максимальная сжимаемая сила, до которой стержень сохраняет прямолинейную форму равновесия или минимальная сжимающая сила, при которой возможна искривленная форма равновесия.

Обобщенная формула Эйлера.

Для классификации других многогранников используется обобщенная формула Эйлера. Если у некоторого многогранника 16 вершин, 32 ребра и 16 граней, то его эйлерова характеристика равна 16 – 32 + 16 = 0. Это позволяет утверждать, что данный многогранник принадлежит классу многогранников, гомеоморфных тору. Отличительной особенностью этого класса является эйлерова характеристика, равная нулю. Более общо, пусть Р – многогранник с N0 вершинами, N1 ребрами и N2 гранями. Говорят, что данный многогранник гомеоморфен поверхности рода n в том и только в том случае, если

Часто момент инерции тела определяют выражением

,

где _u – радиус инерции.

8. Пределы применимости формулы Эйлера. Формула Ясинского. Проектный расчет методом последовательных приближений.

Пределы применимости формулы Эйлера

Формула Эйлера основана на соотношениях, вытекающих из закона Гука. Следовательно, она справедлива при напряжениях меньших предела пропорциональности 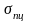. Введем обозначения:

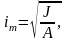
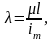(4)

где 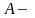площадь сечения, 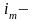минимальный радиус инерции сечения. Безразмерная величина 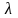зависит от размеров стержня и способа его закрепления и называется гибкостью стержня.

Пределы применимости формулы Эйлера теперь находятся из условия:

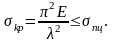
Обозначим

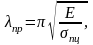
где 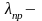предельная гибкость зависит только от свойств материала.

Теперь условие применимости формулы Эйлера примет вид

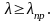
Формула Ясинского

Когда формула Эйлера неприменима (за приделом упругости) для определения критической силы можно воспользоваться эмпирической формулой Ясинского П.Ф.

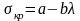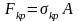, (7)

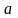Здесь и 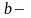коэффициенты, зависящие от материала стержня, измеряются в МПа, приводятся в справочниках: для ст. 3

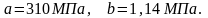
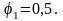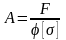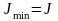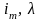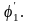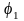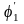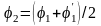Метод последовательных приближений. Задаются Вычисляют по . и в зависимости от формы сечения . Далее по определяют и по таблице Если разница между и большая, то следует повторить расчет, задавшись . Так продолжают до тех пор пока разница между и не будет меньше 3%. Расчет заканчивают проверкой условия прочности