А

Аксиомы статики. Статика базируется на основных законах, принимаемых без математических доказательств и называемых аксиомами статики. Аксиома 1. Если на свободное твердое тело действуют две силы, то тело может находиться в равновесии только тогда, когда эти силы равны по модулю, действуют по одной прямой в противоположные стороны. Аксиома 2. Действие данной системы сил на абсолютно твердое тело не изменяется, если к ней добавить или от нее отнять уравновешенную систему сил. Аксиома 3. При всяком действии одного материального тела на другое со стороны другого тела имеется противодействие, такое же по величине, но противоположное по направлению. Аксиома 4. Две силы, приложенные к твердому телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, построенного на этих силах как на сторонах. Аксиома 5. Механическое состояние не изменится, если освободить ее от связей, приложив к точкам системы силы, равные реакциям связей. Эту аксиому называют аксиомой о связях.

Г

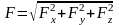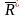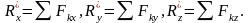1.Графический способ сложения сходящихся сил. Аналитический способ задания и сложения сил. Аналитический способ задания силы заключается в задании координат точек приложения и проекции на оси координат. В этом случае модуль силы равен , а углы между силой и осями координат определяются из выражений Геометрическую сумму системы сил называют главным вектором этой системы – . В проекциях на оси: Тогда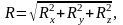

2.Геометрия, силы в зацеплении и расчет конических передач.

Конические передачи применяются для передачи вращения между валами оси которых пересекаются под некоторым углом (обычно 90º). Для нарезания колес необходимы специальные станки и инструменты.

Геометрия передачи и усилия в зацеплении

Рисунок 1

Геометрические параметры передачи:

средний диаметр делительной окружности ;

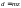внешний диаметр делительной окружности ;

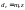внешний диаметр окружности выступов ; (1)

внешнее конусное расстояние;

среднее конусное расстояние ;

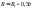b - ширина венца;

- угол делительного конуса,

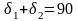º ; .

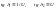Усилия в передаче определяются по формулам

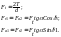
Расчет на контактную и изгибную выносливость

П роверочный расчет конических передач по контактным напряжениям проводится по формуле

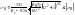, (2)

где коэффициент нагрузки 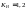при НВ350 и при НВ350.

Проектный расчет по контактным напряжениям производится по формуле, получаемой из (2):

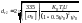, (3)

где _R=в/R_e – коэффициент ширины зубчатого венца; рекомендуется _R=0,285.

Диаметр d_e2 округляется по ГОСТу.

Проверку по напряжениям изгиба проводят по формуле

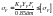, (4)

где коэффициент нагрузки К_F выбирается также, как и для цилиндрических передач, а коэффициент формы зуба Y_F выбирается в зависимости от эквивалентного числа зубьев z_э=z/cos; 0,85 – опытный коэффициент, учитывающий понижение нагрузочной способности конической передачи по сравнению с цилиндрической; m – средний модуль.

Для колес с высокой твердостью поверхности зубьев проектный расчет проводится по напряжениям изгиба:

, (5)

где .

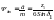Порядок проектного расчета аналогичен

цилиндрическим передачам

15. Геометрия, силы в зацеплении, к.П.Д. И кинематика червячных передач.

Червячная передача применяется для передачи вращения между валами перекрещивающимися в пространстве (обычно под 90º). Она состоит из червяка и червячного колеса. Червячные передачи используются как кинематические (в приборах) и как силовые (в редукторах).

Достоинства:

а) плавность и бесшумность работы;

б) возможность передачи больших мощностей и осуществление большого передаточного

отношения ;

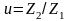в) компактность.

Недостатки:

а) низкий КПД 0.70.9 (износ, трение);

б) высокая стоимость изготовления.

Червячные передачи делятся на передачи с цилиндрическими и глобоидными червяками. По профилю червяка различают червяки с архимедовым (трапециадальным) и эвольвентным профилем. По заходности червяка на 1, 2 и 4 заходные (число винтовых линий).

Геометрия передачи и силы в зацеплении

а) б)

Рисунок 2

Геометрия передачи.

Диаметры делительных окружностей:

,

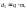
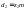где m= q-коэффициент диаметра червяка.

Диаметры окружностей выступов и впадин:

Наибольший диаметр червячного колеса:

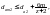
где z₁ - заходность червяка.

Межцентровое расстояние

Длинна нарезной части червяка и ширина венца колеса:

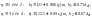
Условный угол обхвата червяка колесом

Угол подъема витка червяка

.

Скорость скольжения

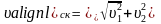или

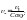
КПД червячного редуктора

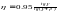, (6)

где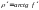 - приведенный угол трения;

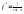- приведенный коэффициент трения.

Силы в передаче:

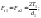
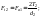(7)

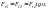
Д

1.Деформации и перемещения при растяжении - сжатии. Коэффициент Пуассона. Потенциальная энергия деформации. При изменении длины бруса изменяются и поперечные размеры сечения. Из опыта установлено, что относительная деформация в поперечном направлении 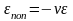, где - коэффициент Пуассона, упругая постоянная материала, определяемая экспериментально. Потенциальная энергия деформации: Из закона сохранения энергии потенциальная энергия деформации 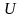равна работе продольных сил на перемещение : .

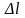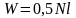Используя формулу 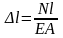, получаем .