Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет пищевых технологий

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Titulka_zmis_vstup_-_kopia 111.doc

Скачиваний:

Добавлен:

01.05.2025

Размер:

613.38 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 87 8 > Следующая >>>

2.3.Розробка і побудова моделей

За наявними даними побудовано графіки залежності показника від кожного фактора, а також побудовано лінію тренда, але тільки для парних моделей.

Лінія тренда – це уявна лінія, навколо якої групуються дослідні дані.

Подальший аналіз кожної моделі виконується за допомогою лінійної функції.

Спочатку розглядається вплив кожного фактора окремо (парні моделі у-х₁; у-х₂; у-х₃), потім двох факторів разом (моделі у-х₁, х₂; у-х₂, х₃; у-х₁, х₃).

Також знаходимо ще одну характеристику тісноти зв’язку між показником і фактором, який називається індексом кореляції – R.

За своїм значенням індекс кореляції збігається з кореляційним відношенням. Тобто, чим ближче R до одиниці, тим тісніший зв’язок між ознаками.

Для оцінки надійності кореляційних характеристик використовується критерій Фішера, який визначається за формулою:

F = ∂² k₂/ ϭ² k₁

де k₁= К - 1; k₂ = n – K – ступені вільності для міжгрупової і середньої з групових дисперсій;

n – кількість елементів досліджуваної сукупності;

К – число груп, на які поділена сукупність.

Фішер знайшов розподіл відношень дисперсій і розробив відповідні математичні таблиці, в яких наводиться F-критерій теоретичний F теоретичний при ймовірностях 0,95 і 0,99. Якщо розрахунковий критерій Фішера більший за табличний з даною ступінню довіри, значить між показником і фактором існує зв’язок з цією ступінню довіри. Якщо ж розрахунковий критерій менший табличного, то різниця між дисперсіями зумовлена впливом випадкових факторів.

2.4. Побудова парних моделей

Парна модель є базовою моделлю впливу кожного фактора.

Побудова виконується двома способами на кожну модель:

за побудовою лінії тренда;
за допомогою статистичної функції Лінійна (глибокий статистичний аналіз).

Загальне рівняння: y = ax + b;

∂y / ∂x = a.

а – коефіцієнт, що визначає швидкість зміни показника від фактора (тобто визначає силу впливу фактора на показник).

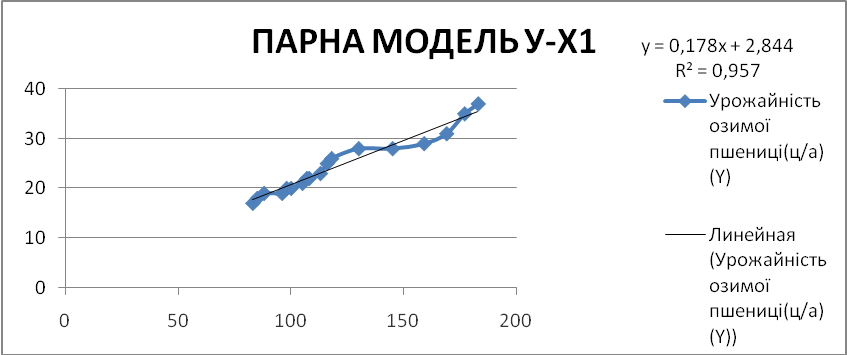
ПАРНА МОДЕЛЬ У-Х1
Роки	Фосфорні добрива (Х1)	Урожайність озимої пшениці(ц/a) (Y)	ТРЕНД	ЛІНІЙНА
1996	83	17	17,618	17,647
1997	85	18	17,974	18,004
1998	88	19	18,508	18,539
1999	96	19	19,932	19,966
2000	98	20	20,288	20,323
2001	100	20	20,644	20,679
2002	105	21	21,534	21,571
2003	107	22	21,89	21,928
2004	108	22	22,068	22,106
2005	113	23	22,958	22,998
2006	116	25	23,492	23,533
2007	118	26	23,848	23,890
2008	130	28	25,984	26,030
2009	145	28	28,654	28,705
2010	159	29	31,146	31,202
2011	169	31	32,926	32,986
2012	177	35	34,35	34,412
2013	183	37	35,418	35,482
			R² = 0,968	0,957

	ФУНКЦІЯ ЛІНІЙНА У-Х1
	а₁	а₀
коеф. Моделі	0,178	2,844
δ	0,009	1,178
R2	0,957	1,247
F,f	358,309	16
Si	557,548	24,897
Фішер табличне	246,464
Оцінка адекватності моделі	модель адекватна

За проведеними розрахунками отримано рівняння y-x₁; y=0,178x+2,844.

За розрахунком критерію Фішера встановлено ступінь адекватності моделі – модель адекватна, оскільки розрахунковий критерій більший за табличного.

Коефіцієнт кореляції становить 0,978, а отже, зв’язок між впливаючим фактором та показником є досить тісним.

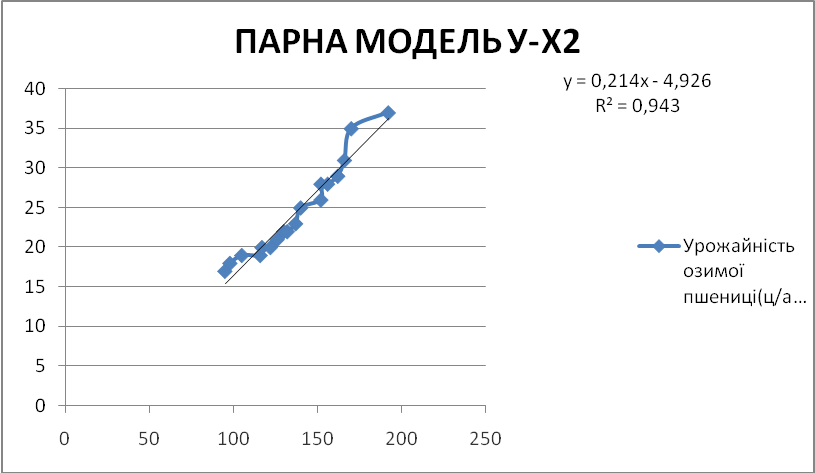
ПАРНА МОДЕЛЬ У-Х2
Роки	Калійні добрива (Х2)	Урожайність озимої пшениці(ц/a) (Y)	ТРЕНД	ЛІНІЙНА
1996	95	17	15,404	15,424
1997	98	18	16,046	16,066
1998	105	19	17,544	17,566
1999	116	19	19,898	19,922
2000	117	20	20,112	20,136
2001	122	20	21,182	21,207
2002	126	21	22,038	22,064
2003	130	22	22,894	22,921
2004	132	22	23,322	23,350
2005	137	23	24,392	24,421
2006	140	25	25,034	25,063
2007	152	26	27,602	27,634
2008	152	28	27,602	27,634
2009	156	28	28,458	28,491
2010	162	29	29,742	29,776
2011	166	31	30,598	30,633
2012	170	35	31,454	31,490
2013	192	37	36,162	36,202
			R² = 0,943	0,943

	ФУНКЦІЯ ЛІНІЙНА У-Х2
	а₂	а₀
коеф. Моделі	0,214	-4,927
δ	0,013	1,836
R2	0,943	1,440
F,f	264,931	16
Si	549,272	33,172
Фішер табличне	246,464
Оцінка адекватності моделі	модель адекватна

За проведеними розрахунками отримано рівняння y-x₂; y=0.214x₂- 4.926.

Коефіцієнт кореляції становить 0,971, а отже, зв’язок між впливаючим фактором та показником є досить тісним.

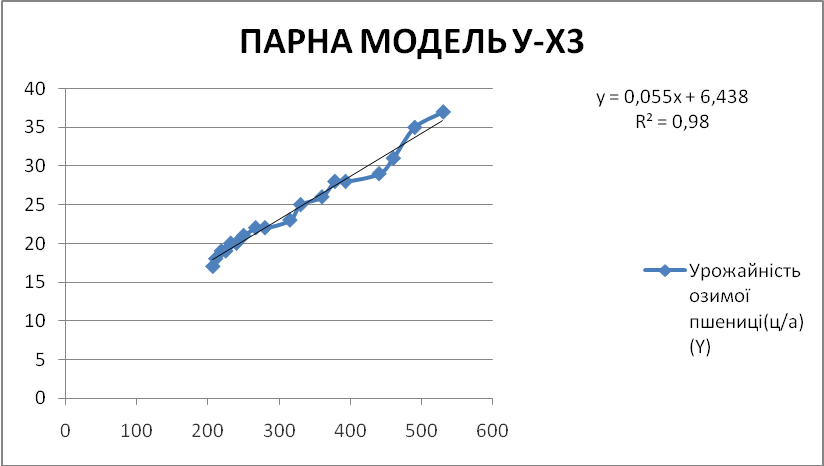
ПАРНА МОДЕЛЬ У-Х3
Роки	Азотні добрива (Х3)	Урожайність озимої пшениці(ц/a) (Y)	ТРЕНД	ЛІНІЙНА
1996	207	17	17,947	17,952
1997	211	18	18,170	18,175
1998	219	19	18,615	18,620
1999	225	19	18,948	18,953
2000	232	20	19,337	19,343
2001	240	20	19,782	19,788
2002	250	21	20,338	20,344
2003	267	22	21,283	21,289
2004	280	22	22,006	22,013
2005	315	23	23,952	23,959
2006	330	25	24,786	24,794
2007	360	26	26,454	26,462
2008	378	28	27,455	27,464
2009	393	28	28,289	28,298
2010	440	29	30,902	30,912
2011	460	31	32,014	32,025
2012	490	35	33,682	33,693
2013	530	37	35,906	35,918
			R² = 0,98	0,980

	ФУНКЦІЯ ЛІНІЙНА У-Х3
	а₃	а₀
коеф. Моделі	0,056	6,438
δ	0,002	0,673
R2	0,980	0,853
F,f	785,039	16
Si	570,811	11,634
Фішер табличне	246,464
Оцінка адекватності моделі	модель адекватна

За проведеними розрахунками отримано рівняння y-x₃; y=0,055x₃+6,438.

За розрахунком критерія Фішера встановлено ступінь адекватності моделі – модель адекватна, оскільки розрахунковий критерій більший за табличного.

Коефіцієнт кореляції становить 0,99, а отже, зв’язок між впливаючим фактором та показником є досить тісним.

Рейтингова таблиця множинних моделей
Моделі	Математична форма	Кореляція	R²	Фішер F	аі	Оцінка впливу фактора	місце у рейтингу якості моделі
Модель У-Х1	y = 0,178x + 2,844	0,978393879	0,957254583	358,309137	0,178351823	рейтинг впливу фактора Х1	добре
Модель У-Х2	y = 0,214x - 4,926	0,971105789	0,943046454	264,9307079	0,214215431	рейтинг впливу фактора Х2	добре
Модель У-Х3	y = 0,055x + 6,438	0,9899626	0,980025949	785,0393219	0,055622521	рейтинг впливу фактора Х3	відмінно

	Місце у рейтингу впливу факторів на показник
	MAX
модель Y-X1	0,980025949	0	місце 2	0
модель Y-X2	0,957254583	0	0	місце 3
модель Y-X3	0,943046454	місце 1	0	0

Найкращою моделю є У-Х3 як має найвищий коефіцієнт детермінації R2. Інші моделі мають також високу якість. Всі моделі є адекватними так як коефіцієнти фішера розрахункові більші за табличне значення. Найкращий вплив фактора прослідковеється в Х3.

2.5.

Побудова множиних моделей

Побудова даних моделей проводиться лише на основі функції Лінійна.

Загальне рівняння має вигляд: y = a₁x₁ + a₂x₂ + b;

∂y / ∂x₁ = a₁;

∂y / ∂x₂ = a₂.

МНОЖИННА-2 МОДЕЛЬ У-Х1-Х2
Роки	Урожайність озимої пшениці (ц/a) (Y)	Фосфорні добрива (Х1)	Калійні добрива (Х2)	Y-розрах
1996	17	83	95	16,535
1997	18	85	98	17,023
1998	19	88	105	17,986
1999	19	96	116	19,845
2000	20	98	117	20,149
2001	20	100	122	20,822
2002	21	105	126	21,718
2003	22	107	130	22,299
2004	22	108	132	22,589
2005	23	113	137	23,578
2006	25	116	140	24,172
2007	26	118	152	25,491
2008	28	130	152	26,757
2009	28	145	156	28,709
2010	29	159	162	30,741
2011	31	169	166	32,165
2012	35	177	170	33,379
2013	37	183	192	36,043

	ФУНККЦІЯ ЛІНІЙНА Y-X1-X2
	а₂	а₁	а₀
коеф. Моделі	0,092	0,106	-0,995
δ	0,031	0,026	1,630
R2	0,973	1,027	#Н/Д
F,f	268,561	15	#Н/Д
Si	566,621	15,824	#Н/Д
Фішер табличне	19,429
Оцінка адекватності моделі	модель адекватна

Отримано рівняння у-х₁, х₂;

y=-1.00+0.11*Х1=0.09*Х2. За R^2 модель – точна. За критерієм Фішера модель адекватна.

МНОЖИННА-2 МОДЕЛЬ У-Х1-Х3
Роки	Урожайність озимої пшениці (ц/a) (Y)	Фосфорні добрива (Х1)	Азотні добрива (Х3)	Y-розрах
1996	17	83	207	17,888
1997	18	85	211	18,129
1998	19	88	219	18,588
1999	19	96	225	19,068
2000	20	98	232	19,454
2001	20	100	240	19,889
2002	21	105	250	20,492
2003	22	107	267	21,363
2004	22	108	280	22,016
2005	23	113	315	23,830
2006	25	116	330	24,628
2007	26	118	360	26,128
2008	28	130	378	27,284
2009	28	145	393	28,366
2010	29	159	440	30,974
2011	31	169	460	32,180
2012	35	177	490	33,822
2013	37	183	530	35,902

	ФУНККЦІЯ ЛІНІЙНА Y-X1-X3
	а₃	а₁	а₀
коеф. Моделі	0,048	0,024	5,896
δ	0,011	0,037	1,092
R2	0,981	0,869	#Н/Д
F,f	378,184	15	#Н/Д
Si	571,118	11,326	#Н/Д
Фішер табличне	19,429
Оцінка адекватності моделі	модель адекватна

Отримано рівняння у-х₁, х₃;

y=5.90+0.02x₁+0.05 x₃.

За критерієм Фішера модель адекватна.

МНОЖИННА-2 МОДЕЛЬ У-Х2-Х3
Роки	Урожайність озимої пшениці (ц/a) (Y)	Калійні добрива (Х2)	Азотні добрива (Х3)	Y-розрах
1996	17	95	207	17,444
1997	18	98	211	17,744
1998	19	105	219	18,381
1999	19	116	225	19,080
2000	20	117	232	19,441
2001	20	122	240	20,002
2002	21	126	250	20,617
2003	22	130	267	21,555
2004	22	132	280	22,231
2005	23	137	315	24,038
2006	25	140	330	24,845
2007	26	152	360	26,689
2008	28	152	378	27,520
2009	28	156	393	28,365
2010	29	162	440	30,764
2011	31	166	460	31,840
2012	35	170	490	33,378
2013	37	192	530	36,067

	ФУНККЦІЯ ЛІНІЙНА Y-X2-X3
	а₃	а₂	а₀
коеф. Моделі	0,046	0,038	4,250
δ	0,008	0,032	1,948
R2	0,982	0,842	#Н/Д
F,f	403,721	15	#Н/Д
Si	571,822	10,623	#Н/Д
Фішер табличне	19,429
Оцінка адекватності моделі	модель адекватна

Отримано рівняння у-х₂-х₃;

y=4.25+0.04*x₂+0.05 x₃.

За критерієм Фішера модель адекватна

Рейтингова таблиця множинних-2 моделей
Номер моделі	Моделі	Математична форма	Кореляція моделі і процесу	R²	Фишер F	a_i	a_j	Оцінка синергізму факторів для a_i	Оцінка синергізму факторів для a_j	Місце у рейтингу впливу факторів на показник	Місце у рейтингу якості моделі
1	Модель У-Х1-Х2	у=-1+0,11Х1+0,09Х2	0,986	0,973	268,561	0,106	0,092	дія Х1 послаблюється	дія Х2 послаблюється	X1 сильніше за Х2	добре
2	Модель У-Х1-Х3	у=5,9+0,02Х1+0,05Х3	0,990	0,981	378,184	0,024	0,048	дія Х1 послаблюється	дія Х3 підсилюється	Х1 слабше за Х3	добре
3	Модель У-Х2-Х3	у=4,25+0,04Х2+0,05Х3	0,991	0,982	403,721	0,038	0,046	дія Х2 послаблюється	дія Х3 послаблюється	Х2 слабше за Х3	відмінно

Автоматичне визначення рейтингу якості моделі
	Max
Модель 1	0,982	0	0	місце 3
Модель 2	0,981	0	місце 2	0
Модель 3	0,973	місце 1	0	0

Модель У-Х1-Х3 є найякіснішою бо має найвищий коефіцієнт детермінації R². Інші моделі також є якісними. Всі моделі є адекватними так як коефіцієнти фішера розрахункові більші за значення фішера табличного. Найсильніша дія фактора спостерігається у фактора Х3 в моделі У-Х2-Х3, також трішки менше в моделі У-Х1-Х3. Інші фактори мають значно менший вплив. Всі фактори взаємопослаблюють одне одного.

Побудова моделей за впливом на показник відразу трьох факторів.

Загальне рівняння: у = а₁х₁ + а₂х₂ + а₃х₃ + b;

∂y / ∂x₁ = a₁;

∂y / ∂x₂ = a₂;

∂y / ∂x₃ = a₃.

	МНОЖИННА-2 МОДЕЛЬ У-Х1-Х2-Х3
Роки	Урожайність(ц/a) (Y)	Фосфорні (Х1)	Калійні (Х2)	Азотні (Х3)	Y-розрах
1996	17	83	95	207	17,37021649
1997	18	85	98	211	17,69032619
1998	19	88	105	219	18,34472366
1999	19	96	116	225	19,20115236
2000	20	98	117	232	19,55903421
2001	20	100	122	240	20,11096075
2002	21	105	126	250	20,77514452
2003	22	107	130	267	21,63480247
2004	22	108	132	280	22,23793864
2005	23	113	137	315	23,9038232
2006	25	116	140	330	24,67227767
2007	26	118	152	360	26,34366482
2008	28	130	152	378	27,33335286
2009	28	145	156	393	28,43714956
2010	29	159	162	440	30,82641408
2011	31	169	166	460	31,99924965
2012	35	177	170	490	33,50780246
2013	37	183	192	530	36,05196642

	ФУНККЦІЯ ЛІНІЙНА У-Х1-Х2-Х3
	а₃	а₂	а₁	а₀
коеф. Моделі	0,039	0,039	0,025	3,654
δ	0,014	0,033	0,037	2,172
R2	0,982	0,857	#Н/Д	#Н/Д
F,f	259,538	14	#Н/Д	#Н/Д
Si	572,157	10,288	#Н/Д	#Н/Д
Фішер табличне	8,715
Оцінка адекватності моделі	модель адекватна

Отримано рівняння у-х₁,х₂,х₃; y=3.65+0.02*х₁+0.04*х₂+0.04 *х₃.

Модель адекватна, оскільки розрахунковий критерій Фішера більший за табличний.

Автоматичне визначення рейтингу якості моделі
	Max
Модель 1	0,982	0	0	місце 3
Модель 2	0,981	0	місце 2	0
Модель 3	0,973	місце 1	0	0

Модель У-Х1-Х3 є найякіснішою бо має найвищий коефіцієнт детермінації R2. Інші моделі також є якісними. Всі моделі є адекватними так як коефіцієнти фішера розрахункові більші за значення фішера табличного. Найсильніша дія фактора спостерігається у фактора Х3 в моделі У-Х2-Х3, також трішки менше в моделі У-Х1-Х3. Інші фактори мають значно менший вплив. Всі фактори взаємопослаблюють одне одного.

ВИСНОВКИ ТА РЕКОМЕНДАЦІЇ

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

Джигирей В . С . Екологія та охорона навколишнього природного середовища: навч . посібн . / В . С . Джигирей. – 2007
Технологія вирощування озимої пшениці / [Електронний ресурс] - Режим доступу до статті:

http://apk-group.com.ua/index.php?option=content&task=view&id=128

<<< < Предыдущая 1 2 3 4 5 67 / 87 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
11.02.20163.53 Mб99teoriya.doc
#
25.11.2019731.65 Кб4Testovi_pitannya_do_ekzamenu_z_istoriyi_Ukrayin...doc
#
01.05.2025130.56 Кб0tez_dopovidey.doc
#
22.11.2019136.19 Кб10The Media.doc
#
20.09.20191.44 Mб5This is FINALE.doc
#
01.05.2025613.38 Кб0Titulka_zmis_vstup_-_kopia 111.doc
#
11.02.20164.43 Mб29TMO_zavershene.doc
#
11.02.201647.1 Кб17TM_GRS.doc
#
11.02.20161.2 Mб72TOV-VO_kharch_prod_L_R_Shulga_Grigorenko_Chor.doc
#
20.09.2019338.04 Кб103tovaroznavstvo.docx
#
01.05.20251.46 Mб0TPRG.doc