2.3.2 Предварительные основные размеры колеса

• делительный диаметр:

;

.

Вычисленный диаметр округляем до стандартного значения /1, таблица 24.1/

• ширина:

Вычисленную ширину колеса округляем до стандартного значения /1, таблица 24.1/

2.3.3 Модуль передачи

Максимально допустимый модуль m_max, мм, определяют из условия неподрезания зубьев у основания:

Минимальное значения модуля m_min, мм, определяют из условия прочности:

где коэффициент К_т=2,810³ для косозубых передач /1, с. 20/;

[]_F=247^.10⁶ Па – допускаемое напряжение изгиба.

Коэффициент нагрузки при расчете по напряжениям изгиба рассчитывается по формуле:

где К_Fυ=1,01 – коэффициент учитывает внутреннюю динамику нагружения по /1, таблица 2.9/.

Коэффициент, учитывающий неравномерность распределения напряжений у основания зубьев по ширине зубчатого венца рассчитывается по формуле:

Коэффициент, учитывающий влияние погрешностей изготовления шестерни и колеса на распределение нагрузки между зубьями равен:

Тогда К_F равен:

Вычислим минимальное значение модуля:

Полученный модуль округляем до стандартного значения /1, с. 21/ m=3.

2.3.4 Суммарное число зубьев и угол наклона

Минимальный угол наклона зубьев косозубых колес

/1, с. 21/.

Суммарное число зубьев

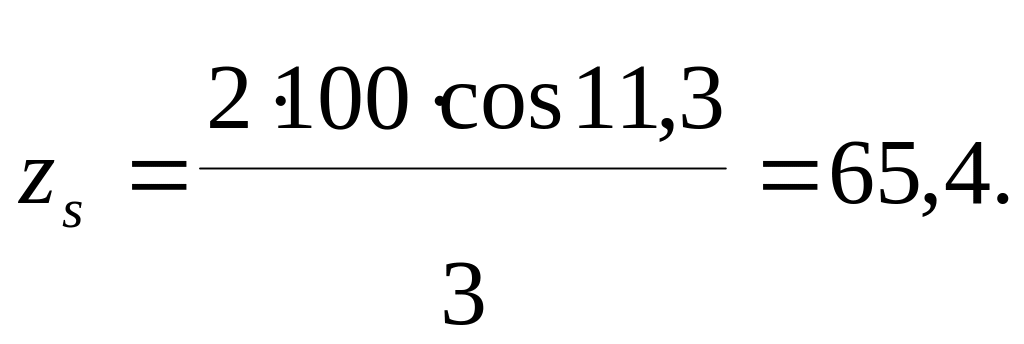
Полученное значение округляем в меньшую сторону до целого числа Z_S=65 и определяем действительное значение угла:

2.3.5 Число зубьев шестерни и колеса

Число зубьев шестерни

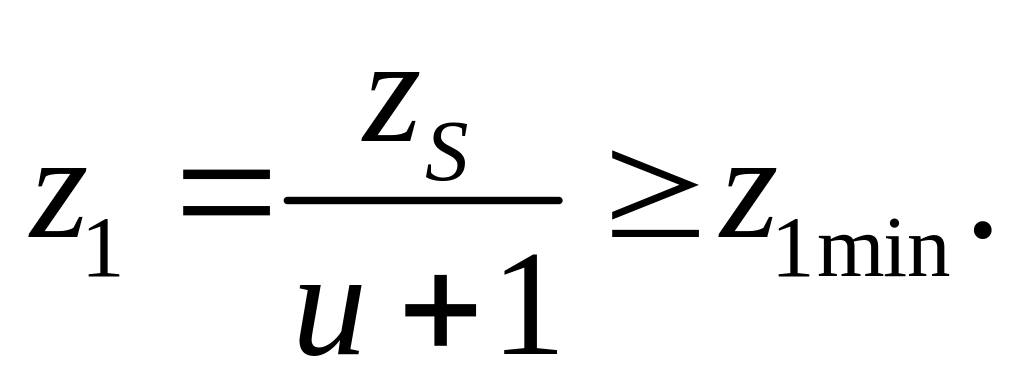
Для косозубых колес z_1min=17cos³ =17 cos³(12,8)=15 [1, с. 21].

Число зубьев колеса внешнего зацепления

2.3.6 Фактическое передаточное число

Отклонение от заданного передаточного числа и=3 составляет 0%, что меньше допускаемому отклонению 4% [1, с. 22].

2.3.7 Диаметры колес

Делительные диаметры d:

• шестерни

• колеса

Диаметры окружностей вершин d_a и впадин d_f зубьев:

• шестерни

- колеса

2.3.8 Проверка зубьев колес по контактным напряжениям

Расчетное контактное напряжение

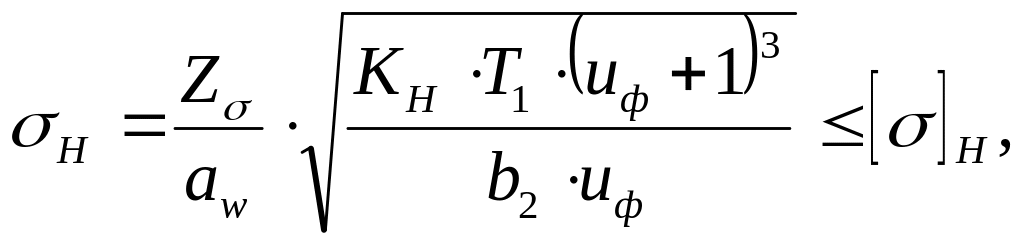
где Z_σ=8400 МПа^1/2 /1, с. 23/.

Расчетное напряжение больше допускаемого в пределах 5%, поэтому ранее принятые параметры передачи принимаем за окончательные.

2.3.9 Силы в зацеплении

• окружная сила

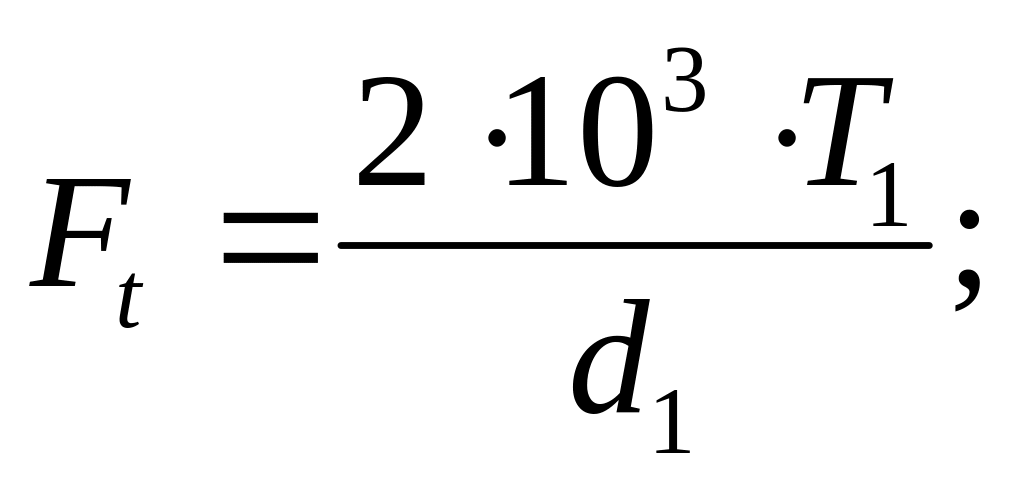
где Т₁ – момент на шестерне, Нм;

• радиальная сила

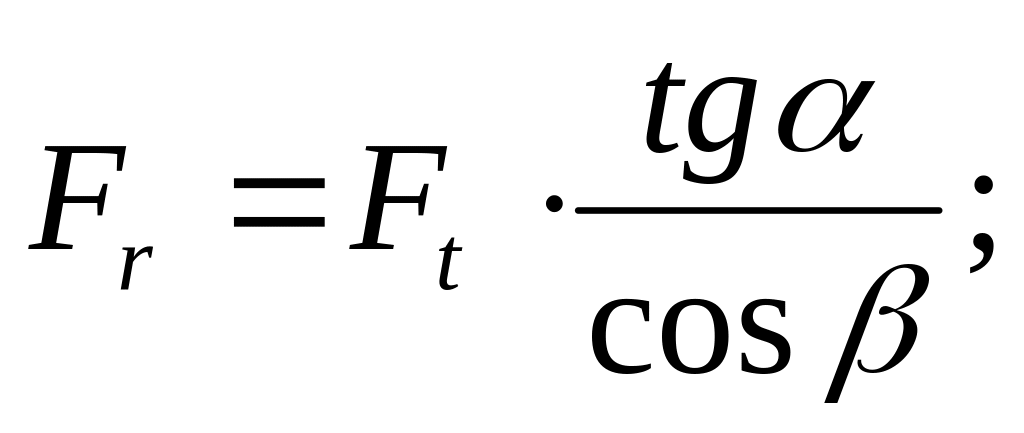
где =20^о для стандартного угла /1, с. 23/;

• осевая сила

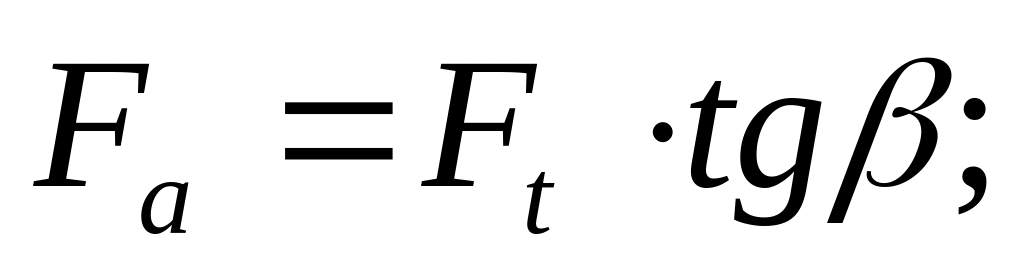
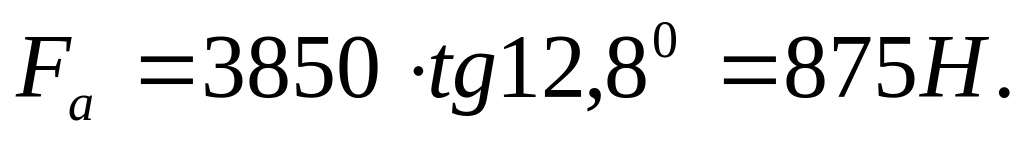
2.3.10 Проверка зубьев колес по напряжениям изгиба

Расчетное напряжение изгиба в зубьях колеса

где - приведенное число зубьев колеса;

Y_Fs2=3,60 [1, таблица 2.10];

- коэффициент, учитывающий угол наклона зуба в косозубой передаче;

Y_ =0,65 – коэффициент, учитывающий перекрытие зубьев /1, с. 24/.

23МПа

Расчетное напряжение изгиба в зубьях шестерни

где приведенное число зубьев шестерни;

Y_Fs1=4,08 /1, таблица 2.10/;

	Ручной счет	Расчет на ЭВМ	Погрешность, %
Межосевое расстояние, мм	100	110	4,8
Передаточное число	3	4,3	17,8
Модуль зацепления	3	2,5	9
Ширина венца колеса, мм	42	48	6,6
Угол наклона зубьев	12,8	12,2	2,4
Окружная сила, Н	3850	3853	0,04
Радиальная сила, Н	1437	1435	0,07
Осевая сила, Н	875	835,8	2,28
Число зубьев: шестерни колеса	16,25 76	16 77	0,77 0,65
Делительный диаметр, мм: шестерни колеса	49,1 150,9	40,9 179,07	9,1 9,08
Диаметр вершин, мм: шестерни колеса	55,1 157	47,43 182,57	7,5 7,53
Диаметр впадин, мм: шестерни колеса	41,6 143,4	36,18 171,32	7 8,9

2.3.11 Сравнительная таблица расчета вручную и на ЭВМ

Таблица 1 – Таблица сравнений.

Расхождения значений передаточного числа при ручном счете и расчете на ЭВМ составили 17,8%. Это связано с тем, что программа ПДМ вела расчет корригированных колес, а ручной счет был рассчитан для некорригированных колес. В связи с этим произошли расхождения в остальных параметрах.

Уточненный расчет тихоходной и быстроходной ступеней выполнен на ЭВМ (приложение А).