Міністерство освіти і науки, молоді та спорту України
Житомирський державний технологічний університет
Кафедра екології
Група ЕО-24м
Реферат
із дисципліни «Системний аналіз якості навколишнього середовища»
на тему: «Статистичний аналіз результатів екологічного досліджень»
Виконала: Гуменюк О. В.
Перевірив: Парфеюк Г. І.
Житомир 2013
Зміст
1. Визначення статистичних характеристик вибіркової сукупності за результатами екологічного спостереження
2. Кореляційний та регресійний аналіз взаємозв’язку між результуючими та факторіальними ознаками
1. Визначення статистичних характеристик вибіркової сукупності за результатами екологічного спостереження
Вибіркова сукупність проведена за результатами екологічних спостережень характеризується наступними показниками.
Варіанта (Х) – окреме значення варіюючої ознаки.
Частота (f) – число варіант (випадків), які мають однакове значення.
Чисельність ряду або об’єм вибірки (n) – сума всіх частот, число об’єктів ряду (n=∑f).
Розмах варіювання – інтервал між найбільшими (xmax) і найменшим (xmin) варіантом ряду (xmax- xmin).
Відхилення
окремих значень варіант від середнього
арифметичного прийнятого позначати
(х-
),
квадрати відхилень
,
суму відхилень і суму квадратів відхилень
і
.
Основними статистичними характеристиками (параметрами) кількісного варіаційного ряду є:
1.
Середня арифметична (
.
2. Дисперсія (S2).
3. Стандартне відхилення (S).
4. Коефіцієнт варіації (v).
5. Похибка середньої арифметичної (S ).
6. Інтервальна оцінка середньої арифметичної генеральної сукупності (довірний інтервал).
7. Відносна похибка вибіркової середньої (точність).
Виконання роботи.
Обробка результатів варіаційного ряду кількісної мінливості зводиться до наступних етапів:
1. Визначення розмаху варіювання (R).
2. Групування вибіркової сукупності із визначенням кількості груп (К).
3. Обчислення групового інтервалу (і).
4. Групове аранжування.
5.
Визначення середнього значення групи
(
).
6. Побудова варіаційного ряду.
7. Розробка допоміжної таблиці.
8. Визначення з допомогою допоміжної таблиці статистичних характеристик (параметрів) кількісного варіаційного ряду.
Вибіркову сукупність кількісної мінливості характеризує 48 варіант довжини колоса озимої пшениці. Зведені показники вибіркової сукупності записують в таблицю:
Таблиця 1
Довжина колосу озимої пшениці
7,4 |
7,8 |
8,2 |
7,7 |
8,4 |
6,3 |
7,8 |
8,3 |
9,4 |
8,5 |
8,3 |
7,2 |
7,1 |
10,5 |
8,4 |
7,3 |
9,6 |
8,5 |
7,1 |
7,5 |
8,2 |
9,1 |
7,6 |
8,4 |
5,5 |
9 |
8,7 |
7,3 |
7,5 |
8,2 |
8,7 |
7,1 |
7,5 |
7,7 |
7,5 |
5,5 |
9,5 |
7,1 |
7,8 |
7,9 |
8,5 |
10,4 |
7,1 |
5,2 |
6,4 |
6,8 |
5,3 |
6,4 |
Послідовність розрахунку.
Аналіз даних вибіркової сукупності ведеться в такій послідовності:
1. Серед 48 показників (варіант) знаходимо мінімальне і максимальне значення довжини колоса:
xmin=5,2 см
xmax=10,5 см
2. Визначити розмах варіювання (R):
см
3. Встановити кількість груп (k):
груп
4. Обчислити груповий інтервал (і):
см
5. Виписати групи за наростанням їх значення:
- початок першої групи встановлюється, виходячи з мінімального значення варіанти – 5,2 см;
- кінець першої групи, або їх верхня межа встановлюється шляхом додавання значення інтервалу групи (і) до нижньої межі групи: 5,2см+0,8см=6см.
Для уникнення суб’єктивних похибок при рознесенні необхідно значення верхніх меж кожної групи зменшити на величину, що показує, з якою точністю виміряна ознака. В нашому прикладі ознака визначалася з точністю 0,1 см враховуючи це, межі груп записують так:
5,2 см -5,9 см
6 см – 6,7 см
6,8 см – 7,5 см
7,6 см – 8,3 см
8,4 см – 9,1 см
9,2 см – 9,9 см
10 см – 10,5 см
6. Наступним етапом є визначення середнього значення групи ( ). Воно дорівнює напівсухі меж груп. Так, для першої групи складає:
см
Подібно визначають середнє значення інших груп.
см
см
см
см
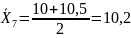см
см
7. Встановивши межі груп і їх середнє значення, приступають до рознесення кожної із 48 варіант до певної груп. Так, в таблиці 1 першою варіантою є 7,4 см. Вона за значенням належить до третьої групи, друга варіанта – 7,8 см, вона відноситься до четвертої групи, третя варіанта – 8,2 см, яка за величиною також відноситься до четвертої групи. Так ведуть рознесення усіх інших варіант. Для спрощення підрахунків кількості спостережень в межах кожної групи користуються позначенням «конверт»:
Схема запису кількості спостережень в групі
Рознесення варіант по групах та визначення частоти групи (f) ведеться за такою таблицею:
Таблиця 2
Рознесення варіант по групах
Група, см |
Середина групи, Х |
Кількість спостережень в формі « конверта» |
Частота, f |
5,2-5,9 |
5,5 |
|
4 |
6-6,7 |
6,3 |
|
3 |
6,8-7,5 |
7,1 |
|
14 |
7,6-8,3 |
7,9 |
|
11 |
8,4-9,1 |
8,7 |
|
10 |
9,2-9,9 |
9,5 |
|
4 |
10-10,5 |
10,2 |
|
2 |
|
|||
8. На підставі середніх значень груп (Х) та їх частот (f) будують варіаційний ряд, в якому вказують значення варіюючої величини (Х) та відповідним її частоти (f).
х |
5,5 |
6,3 |
7,1 |
7,9 |
8,7 |
9,5 |
10,2 |
f |
4 |
3 |
14 |
11 |
10 |
4 |
2 |
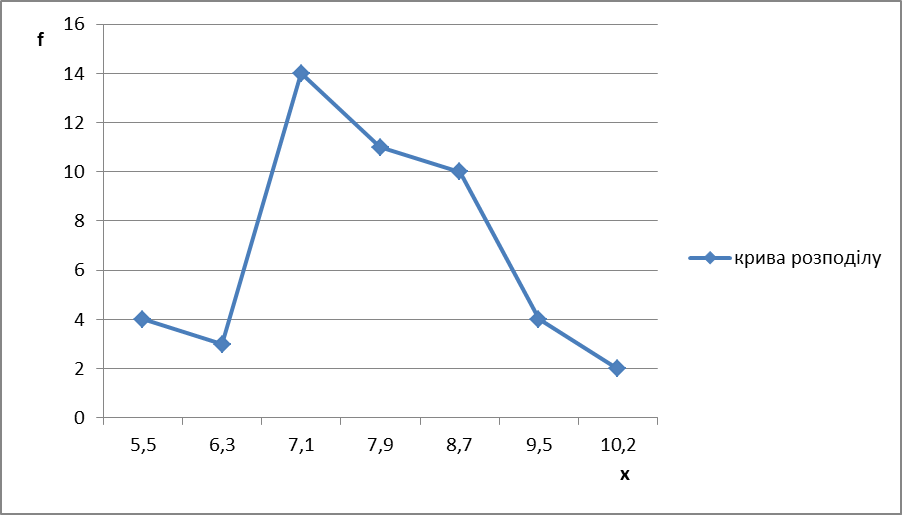
9. Особливості варіаційного ряду можна зобразити графічно. Координатами такого графіка є вісь абсцис, на якій відкладають в довільному масштабі значення середини груп (Х) та вісь ординат, на якій відкладають частоти (f).
На місцях перетину значення Х і f ставлять крапки, які потім з’єднують лініями.
Рисунок 1
Крива Гауса
Рисунок 2
Гістограма
Крім вище наведеної загальної оцінки вибіркової сукупності ведеться також і більш детальний аналіз варіаційного ряду з обчисленням таких статистичних характеристик:
- середньої арифметичної
- дисперсії S2
- стандартного відхилення S
- помилки середньої арифметичної S
- коефіцієнта варіації v
-
інтервальної оцінки середньої арифметичної
генеральної сукупності (довірчий
інтервал)
