Геометрия - ФГОС - 1 семестр - 2012-2013 у.г.
1.Укажите верное определение коллинеарных векторов
(один ответ)
1) равны по длине и сонаправлены
2) лежат на параллельных прямых или на одной прямой
3) равны по длине и противоположны по направлению
4) параллельны некоторой плоскости
2.Укажите верное определение компланарных векторов
(один ответ)
1) Равны по длине и сонаправлены
2) лежат на параллельных прямых или на одной прямой
3) равны по длине и противоположны по направлению
4) параллельны некоторой плоскости
3.Укажите верное определение равных векторов
(один ответ)
1) Равны по длине и сонаправлены
2) лежат на параллельных прямых или на одной прямой
3) равны по длине и противоположны по направлению
4) параллельны некоторой плоскости
4.Укажите верное определение противоположных векторов
(один ответ)
1) равны по длине и совпадают по направлению
2) лежат на параллельных прямых или на одной прямой
3) равны по длине и противоположны по направлению
4) параллельны некоторой плоскости
5.Каким из перечисленных свойств нуль-вектор НЕ обладает:
(один ответ)
1) имеет нулевую длину
2) коллинеарен любому вектору
3) перпендикулярен любому вектору
4) линейно зависимая система не может содержать нулевого вектора
6.Свойством коммутативности НЕ обладает
(один ответ)
1) сложение векторов
2) скалярное произведение
3) умножение вектора на число
4) векторное призведение
7.
Вектор
при
l<0:
(один ответ)
1)
больше
по длине
2) сонаправлен вектору
3) меньше вектора по длине
4) противоположно направлен вектору
8.Вектор при l>0
(один ответ)
1) Больше по длине
2) сонаправлен вектору
3) меньше вектора по длине
4) противоположно направлен вектору
9.Скалярное произведение векторов равно нулю тогда и только тогда, когда векторы
(один ответ)
1) коллинеарны
2) взаимно перпендикулярны
3) компланарны
4) нулевые
10.Векторное произведение векторов равно нулю тогда и только тогда, когда векторы:
(один ответ)
1) Коллинеарны
2) взаимно перпендикулярны
3) компланарны
4) нулевые
11.Смешанное произведение векторов равно нулю тогда и только тогда, когда векторы:
(один ответ)
1) Коллинеарны
2) взаимно перпендикулярны
3) компланарны
4) нулевые
12.Система
векторов
является линейно зависимой, если:
(один ответ)
1)
существуют числа
хотя
бы одно из которых ненулевое, что
выполняется равенство:
;
2) не один из векторов системы нельзя представить в виде линейной комбинации остальных;
3) линейная комбинация векторов этой системы равна нуль-вектору только при равенстве всех коэффициентов нулю;
4) эта система не содержит нулевого вектора.
13.Система векторов является линейно НЕзависимой, если:
(один ответ)
1) Существуют числа хотя бы одно из которых ненулевое, что выполняется равенство: ;
2) хотя бы один из векторов системы можно представить в виде линейной комбинации остальных;
3) линейная комбинация векторов этой системы равна нуль-вектору только при равенстве всех коэффициентов нулю;
4) эта система содержит нулевой вектор.
14.Упорядоченная линейно независимая система векторов, такая что любой вектор пространства является линейной комбинацией векторов этой системы, называется
(один ответ)
1) ортогональной системой;
2) системой координат;
3) базисом
4) репером
15.Размерностью пространства называется
(один ответ)
1) его длина, ширина и высота;
2) количество векторов в базисе;
3) количество векторов в пространстве;
4) количество базисов пространства.
16.Коэффиценты в разложении вектора по базису называются
(один ответ)
1) координатами
2) скалярами
3) ортами
4) определителями
17.Векторы ортонормированного базиса:
(один ответ)
1) равные и взаимно перпендикулярные;
2) компланарные
3) единичные и взаимно перпендикулярные;
4) единичные и коллинеарные.
18.Длина
вектора
,
заданного своими координатами (а1,а2,а3)
в ортонормированном базисе, вычисляется
по формуле:
(один ответ)
1)
=
2)
3)
4)
19.Модуль векторного произведения векторов равен:
(один ответ)
1)
;
2)
;
3)
;
4)
20.Если
векторы
заданы
своими координатами в ортонормированном
базисе, то скалярное произведение можно
найти по формуле:
(один ответ)
1)
;
2)
;
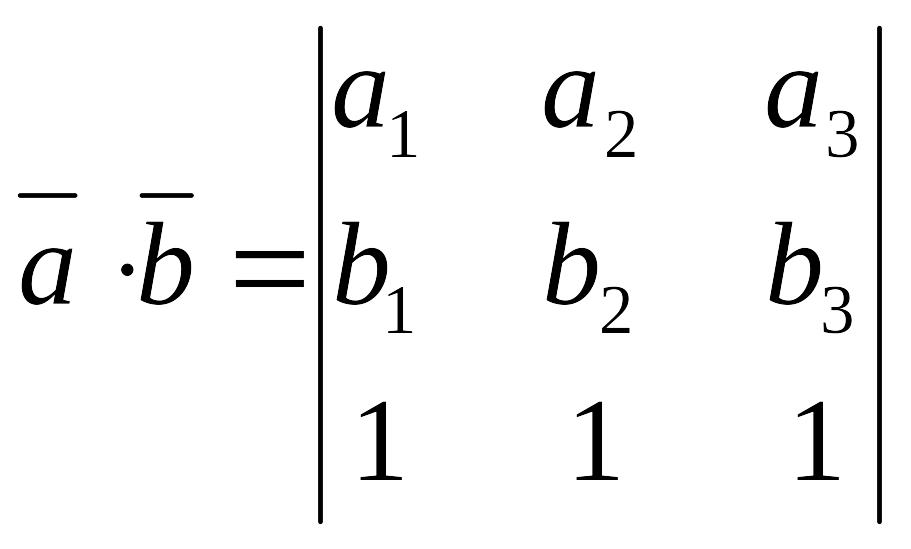3)
;
4)
.
21.Если
векторы
заданы
своими координатами в ортонормированном
базисе, то координаты векторного
произведения.
можно найти по формуле:
(один ответ)
1)
(
);
2)
;
3)
;
4)
22.Направляющие косинусы вектора удовлетворяют следующему соотношению.
(один ответ)
1)
2)
;
3)
;
4)
.
23.Тройка векторов является правой, если:
(один ответ)
1) смешанное произведение векторов положительно;
2) базисные векторы единичны и взаимно перпендикулярны;
3) смешанное произведение векторов отрицательно;
4) векторы компланарны.
24.Векторное произведение векторов применяют для вычисления:
(один ответ)
1) площади параллелограмма и треугольника;
2) площади круга и длины окружности ;
3) объема параллелепипеда и тетраэдра;
4) величины многогранного угла.
25.Смешанное произведение векторов применяют для вычисления:
(один ответ)