Поверхности 2 порядка.

74. Составить уравнение сферы, если она проходит через точку и имеет центр в точке .

75. Составить уравнение сферы, если она имеет центр в точке и касается плоскости .

76. По какой линии пересекается конус с плоскостями:

1) у=3;

2) z=1;

3) x=0?

77. Какую поверхность определяет уравнение

1) ; 2) ; 3) ; 4) ; 5) ;

6) ; 7) ; 8) ; 9) ; 10) ?

Построить эти поверхности.

78. Установить, какие поверхности определяются следующими уравнениями, и построить эти поверхности:

а). б)

в). г).

79. Составить уравнение поверхности, полученной от вращения прямой

линии вокруг оси Ох.

80. Составить уравнение поверхности, полученной от вращения кривой

линии вокруг оси Ох.

81. Составить уравнение поверхности, полученной от вращения прямой

линии вокруг оси Оy.

82. Перейдя к параметрическому заданию прямой, найти точки пересечения поверхности и прямой:

1) и ;

2) и ;

3) и .

83. Приведите уравнение поверхности 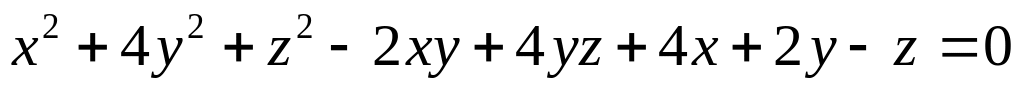к каноническому виду.

Модуль 3 Раздел 4 – Комплексные числа.

84. Изобразить на плоскости комплексного переменного область, заданную неравенствами

85. Представьте в тригонометрической и показательной формах числа, заданные в алгебраической форме: а) , б) .

86. Пусть , 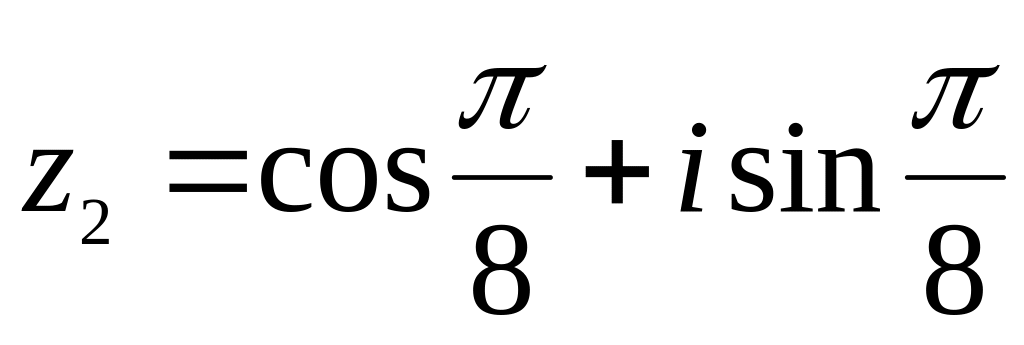. Вычислите , .

87. Изобразите на рисунке множество точек комплексной плоскости, удовлетворяющих условию .

88. Решить уравнение, изобразить все корни на комплексной плоскости.

89. Найти , если .

90. Решите в комплексных числах уравнение .

91. Изобразите на комплексной плоскости числа: , , , , , .

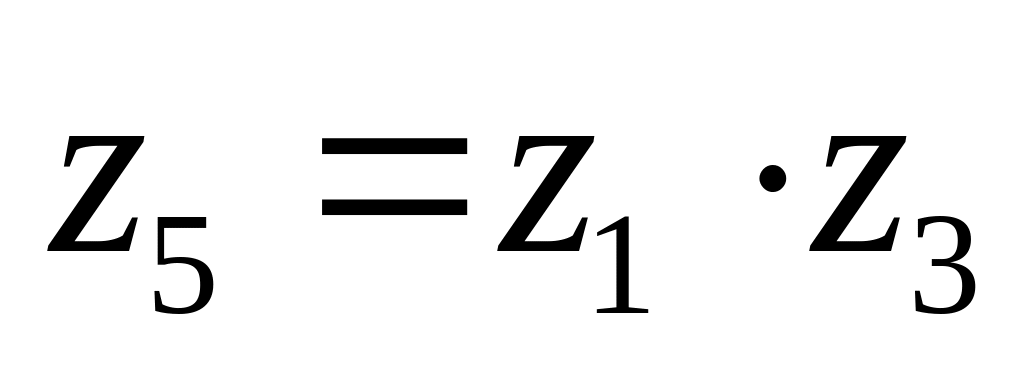92. Дано: , .

Найти: а) ; б) .

93. Решите уравнение .

94. При каких и числа и будут равными?

95. Найдите значения .

Математический анализ

Тренировочные задачи и упражнения

Модуль 1. Дифференциальное исчисление функции одной и нескольких переменных.

Теория пределов.

1.1 Доказать, что предел последовательности lim .

Решение. Пусть при n > N верно , т.е. . Это верно при , таким образом, если за N взять целую часть от , то утверждение, приведенное выше, выполняется.

1.2 Доказать, что последовательность {x_n}= монотонная возрастающая.

Решение. Найдем член последовательности {x_n+1}=

Найдем знак разности: {x_n}-{x_n+1}=

, т.к. nN, то знаменатель положительный при любом n.

Таким образом, x_n+1 > x_n. Последовательность возрастающая, что и следовало доказать.

1.3 Найти предел .

Решение. При подстановке значения х, получаем неопределенность . Разделим каждое слагаемое числителя и знаменателя на х⁴:

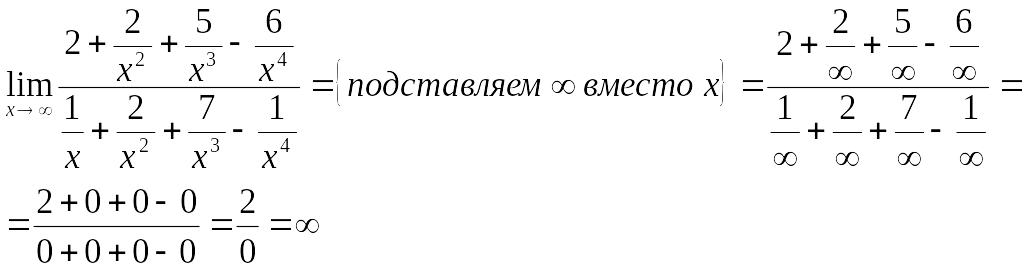
1.4 Найти предел .

Решение. При подстановке значения х, получаем неопределенность . Для нахождения этого предела разложим на множители числитель и знаменатель данной дроби.

x² – 6x + 8 = 0; x² – 8x + 12 = 0;

D = 36 – 32 = 4; D = 64 – 48 = 16;

x₁ = (6 + 2)/2 = 4; x₁ = (8 + 4)/2 = 6;

x₂ = (6 – 2)/2 = 2 ; x₂ = (8 – 4)/2 = 2;

Тогда

1.5 Найти предел

Решение. При подстановке значения х, получаем неопределенность . Умножим числитель и знаменатель дроби на сопряженное выражение: =

= .

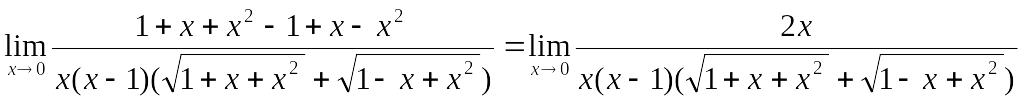6. Найти предел .

Решение. Для вычисления предела воспользуемся Первым замечательным пределом

1.7 Найти предел .

Решение. Для вычисления предела воспользуемся Вторым замечательным пределом

1.8 Найти предел

Решение. Так как tg5x ~ 5x и sin7x ~ 7x при х  0, то, заменив функции эквивалентными бесконечно малыми, получим:

1.9 Найти предел .

Решение.

Так как 1 – cosx = при х0, то .

1.10 Найти предел .

Решение. Так как ~ при , то

1.11 Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.

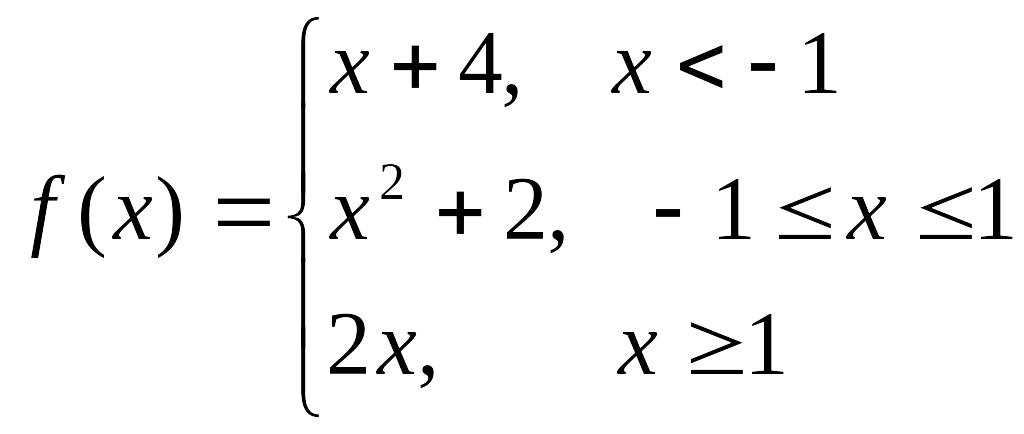
Решение.

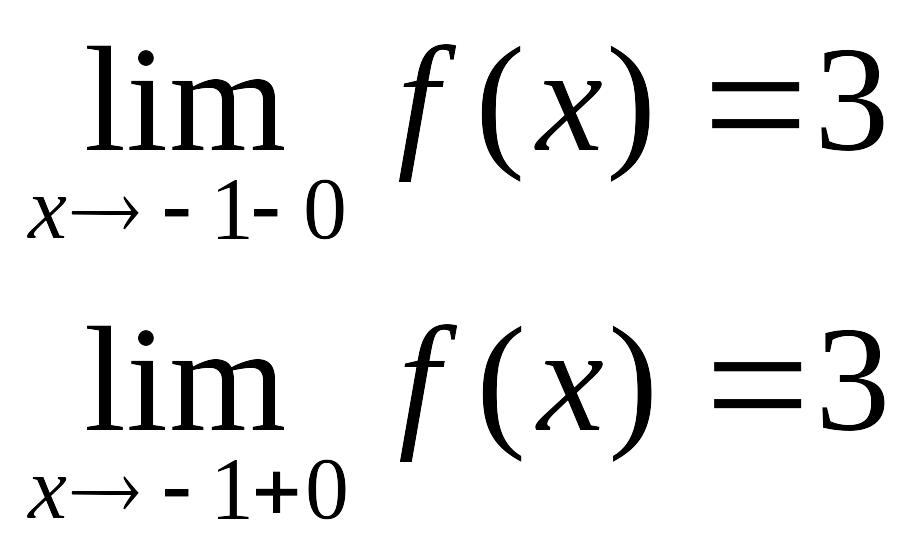
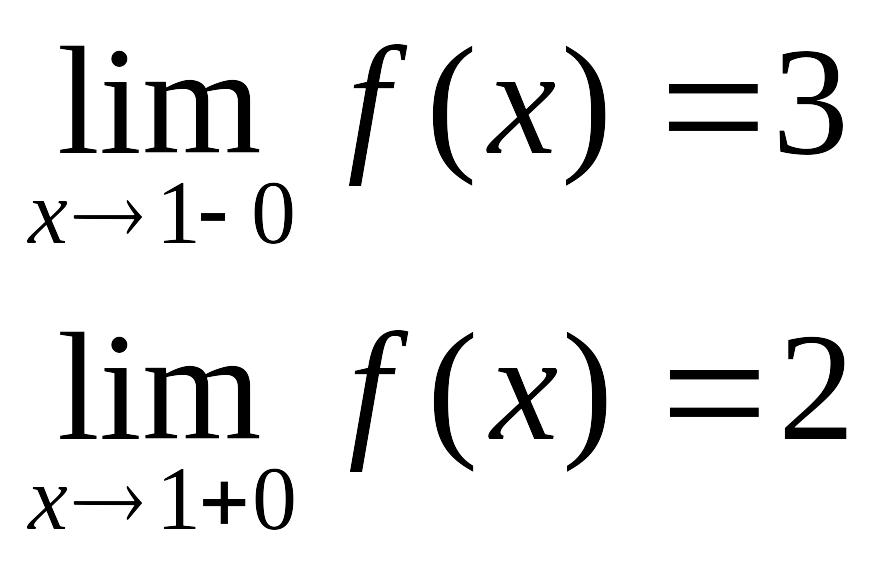
в точке х = -1 функция непрерывна в точке х = 1 точка разрыва 1 – го рода