4. Для заданных множеств А и В найти : а) б) в) г) А= 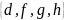В=

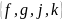
5. Упростить формулу

Билет № 16

Дисциплина «Дискретная математика»

1. Бинарные отношения , способы задания, обратное отношение, примеры.

2. Комбинаторика. Сочетания, примеры использования сочетаний при решении комбинаторных задач..

3. Заданное множество записать через характеристическое свойство.

M=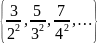

4. Опираясь на определение равенства двух множеств через блок-схемы доказать равенство: AÈ(BÇC)=(AÈB)Ç(AÈC)

5. Упростить формулу:

Билет № 17

Дисциплина «Дискретная математика»

1. Дополнение отношений, равные отношения.примеры.

2. Размещения и перестановки, примеры применения.

3. Какими из свойств соответствия ( инъекция, биекция, сюръекция) обладают заданные соответствия:

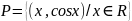Q=

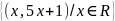
4. Будет ли отношение R рефлексивным, симметричным, транзитивным

M={1; 2; 3; 4} – основное множество

R=

5. Упростить формулу

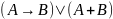
Билет № 18

Дисциплина «Дискретная математика»

1. Операции над бинарными отношениями.

2. Размещения с повторениями, перестановки с повторениями. Примеры.

3. Заданное множество записать через его элементы.

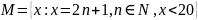
4. Какими из свойств соответствия ( инъекция, биекция, сюръекция) обладают заданные соответствия:

Q=

5. Упростить формулу

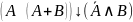
Билет № 19

Дисциплина «Дискретная математика»

1. Бинарные отношения, свойства отношений ( рефлексивность, симметричность, транзитивность). Примеры.

2. Операции вычитания и дополнения между множествами. Примеры.

3. Для данного множества 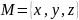: а) составить булеан ( т.е., множество всех подмножеств);б) какое-нибудь покрытие; в) какое – нибудь разбиение.

4. Будет ли отношение R рефлексивным, симметричным, транзитивным

M={1; 2; 3; 4} – основное множество

R=

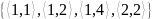
5. Упростить формулу :

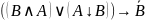
Билет № 20

Дисциплина «Дискретная математика»

1. Отношение эквивалентности, эквивалентные классы.Примеры.

2. Графы. Определение.Свойства.

3. Данное множество записать через характеристичекое свойство:

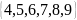
4. Доказать равенство множеств с помощью построения блок-схемы:

AÈ(BÇC)=(AÈB)Ç(AÈC)

5. Упростить формулу

Билет № 21

Дисциплина «Дискретная математика»

1. Отношения порядка, примеры.

2. Основные типы графов.

3. Заданное множество записать через его элементы.

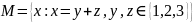
4. Будет ли отношение R рефлексивным, симметричным, транзитивным?

M={1; 2; 3; 4} – основное множество

R=

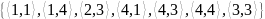
5. Упростить формулу:

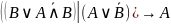
Билет № 22

Дисциплина «Дискретная математика»

1. Высказывания и опреации над высказываниями.

2. Путь в графе (цепь), контуры (циклы).

3. Для данного множества M= 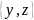: а) составить булеан ( т.е., множество всех подмножеств);б) какое-нибудь покрытие в) какое – нибудь разбиение

4. Будет ли отношение R рефлексивным, симметричным, транзитивным?

M={1; 2; 3; 4} – основное множество

R=

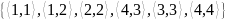
5. Все операции в формуле записать через стрелку Пирса:

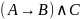
Билет № 23 Дисциплина «Дискретная математика»

1. Конъюнкция, дизъюнкция, отрицание высказывания, свойства данных операций.

2. Представление графа через матрицы. Матрицы смежности и инцидентности. Примеры.

3. Записать данное множество через характеристическое свойство:

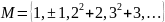
4. Будет ли отношение R рефлексивным, симметричным,

транзитивным ? M={1; 2; 3; 4} – основное множество

R=

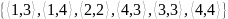
5. Представить запись эквивалентной формулы через операцию штриха Шеффера:

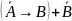
Билет № 24

Дисциплина «Дискретная математика»