
- •Билет № 1 Дисциплина «Дискретная математика»
- •Билет № 2 Дисциплина «Дискретная математика»
- •Для заданных множеств а и в найти : а) б) в)
- •Билет № 3 Дисциплина «Дискретная математика»
- •С помощью эквивалентных преобразований определить сднф для
- •Билет № 6 Дисциплина «Дискретная математика»
- •Построить таблицу истинности для формулы:
- •Билет №9 Дисциплина «Дискретная математика»
- •Билет № 14 Дисциплина «Дискретная математика»
- •Упростить формулу
- •Билет № 23 Дисциплина «Дискретная математика»
- •Заданное множество записать через его элементы.
- •Какими из свойств соответствия ( инъекция, биекция, сюръекция) обладают заданные соответствия:
- •Какими из свойств соответствия ( инъекция, биекция, сюръекция) обладают заданные соответствия:
Билет № 1 Дисциплина «Дискретная математика»
Множества и способы их задания. Примеры.
Операции штриха Шеффера и стрелка Пирса, свойства данных опреаций.
С помощью эквивалентных преоразований определить СДНФ для формулы
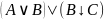
Для заданных множеств А и В найти : а)
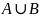 б)
б)
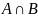 в)
в)
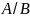
г)
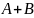 .
А=
.
А= ; В=
; В=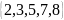
Построить таблицу истинности для заданной формулы.
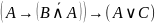
---------------------------------------------------------------------------------------------------------------------------------
Билет № 2 Дисциплина «Дискретная математика»
Подмножества, булеан. Примеры.
Опреация сложения по модулю 2 между высказыванями, свойства данной операции, определить связь с другими операциями.
Задать данное множество через характеристическое свойство.
M=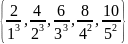
Для заданных множеств а и в найти : а) б) в)
г)
. А=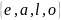 В=
В=
С помощью эквивалентных преобразований определить СДНФ для
формулы

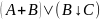
Билет № 3 Дисциплина «Дискретная математика»
Равные множества. Методы доказательства равенства множеств. Примеры.
Построение таблиц истинности для формул от двух и трех переменных, доказательство эквивалентности формул. Привести примеры.
Записать заданное множество поэлементно.
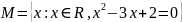
Доказать равенство множеств через построение блок-схем, опираясь на определения, свойства :
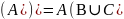
Построить таблицу истинности для формулы: ((A∨B) →
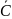 )
→A
)
→A
------------------------------------------------------------------------------------------------
Билет № 4
Дисциплина «Дискретная математика»
Конечные и бесконечные множества. Примеры.
Алгебра Буля. Основные формулы эквивалентности.
Записать множество через характеристическое свойство:
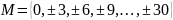
Для заданных множеств А и В найти : а) б) в) г) . А=
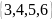 В=
В=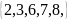
С помощью эквивалентных преобразований определить сднф для
формулы
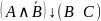
Билет № 5
Дисциплина «Дискретная математика»
Операции над множествами. Законы, связанные с операциями пересечения и объединения. Доказательство одного из законов.
Эквивалентные преобразования формул высказываний.
Для данного множество: а) составить булеан ( т.е., множество всех подмножеств);б) какое-нибудь покрытие в) какое – нибудь разбиение для
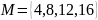
Для заданных множеств А и В найти : а) б) в) г) . А=
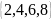 В=
В=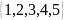
Построить таблицу истинности для формулы:
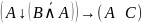
Билет № 6 Дисциплина «Дискретная математика»
Операции вычитания, дополнения и симметричного вычитания над множествами. Примеры.
Упрощение формул с помощью эквивалентных преобразований. Привести примеры.
Записать данное множество через его элементы.
Опираясь на определение равенства двух множеств через блок-схемы доказать равенство:
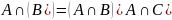
С помощью эквивалентных преоразований определить СДНФ для
Формулы:
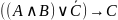
Билет № 7
Дисциплина «Дискретная математика»
Свойства операций над множествами. Доказать одно из свойств.
Булевы функции от одной и двух пременных.
Задать множество через характеристическое свойство:

