Атом ядросы. Ядролық күштер.Альфа, бета, гамма сәуле шығаруының пайда болуы мен заңдылықтары. Атом ядроларының радиоактивті айналуы.

Атом ядросы оң зарядталған протонннан және заряды жоқ нейтроннан тұрады. Бұл бөлшектерді нуклондар деп атайды.

Протон. Протонның массасы mp =938,26 МэВ немесе mp=1836mэ. Спині s=1/2. Магнит моменті мр= +2,79мя, мұндағы мя ядролық магнетон.

Нейтрон. Нейтронның массасы mn=939.26 МэВ. Спині s=1/2. Магнит моменті мn= -1,91 мя. «-» таңбасы механикалық моменті мугнит моментіне қарама-қарсы екенін көрсетеді. Ядролық бөлшектерін массасы массалық атомдық бірлігімен өлшенеді. 1м.а.б.= 1,66*10-27 кг. Мұндағы протондар саны атом қабықшасындағы электрондар манына тең. Олай болса ядродағы протондар саны Менделеев кестесіндегі z элементінің атомдың нөміріне тең. Заряды +ze. Массалық саны A=Z+N, N – нейтрондар саны. Химиялық белгісі ZXA7 Егер атом ядросының зарядтар саны бірдей, ал массаларының саны әртүрлі болса, ядролар изотоптар деп аталады. Керісінше массалар саны бірдей болып, арядтар саны әр түрлі болса изобаралар д.а. Нейтрондары бірдей болса изотоптар қатарын түзейді. Z пен A бірдей, бірақ жартылай ыдырау периодтары әр түрлі ядроларды изомерлық ядролар д.а. Ядро радиосы шамамен 10-15 м.

Ядролық күш. Атом ядросындағы нуклондар арасындағы тартылыс күштерін ядролық күш д.а. Олардың мынадай қасиеттері болады:

1.Я.К-дің әсер ету арақашықтығы шамамен r=10-15м.

2.Бұл күштер қанығу қасиетіне ие болады. Бір нуклон белгілі нуклондармен ғана әсерлеседі.

3.Я.К. нуклондардың зарядына байланысты емес.

4.Бұл күштер табиғатта кездесетін күштердің ең қуаттысы, электромагниттік күштерден 100 есе артық.

5.Я.К-тер центрлік күштер қатарына жатпайды. Я.К-тер, нуклондардың спиндерінің бағытына тәуелді.

Радиактивті құбылыс – атомдардың өздігінен сәуле шығаруы. Радиоактивті сәуле шығаратын заттар қасиеті радиоактивтік д.а. Радиактивтік элементтердің (уран, радий, торий т.б.) атомдары альфа, бета, гамма – сәулелерін шығара отырып, басқа бір элемент атомына айналады. Орнықсыз ядролардың белгілі уақыт аралығында орнықты күйге келіп үлгеретін шамасын көрсететін заңдылықты радиоактивтік заңдылықты радиоактивтік ыдырау заңы д.а.

Альфа, бета, гамма-сәулелері

альфа-бөлшектер ағыны. Альфа-бөлшек гелий ядросы ботып табылады. Заряды 2е, жылдамдығы (1,5-2)*107 м/с. Энергиясы Е=4 2 МэВ. Ыдырау формуласы

Өтімділік қабілеті өте аз. Спектрлері дискретті. Ядродан шығатын а-бөлшек энергиясы жоғары потенциал тосқауылдан жарып өтеді.

2. В-бөлшек ағыны. В-бөлшек электрондар ағыны. Жылдамдығы жарық жылдамдығына жуық. Энергиясы Е=0,001 3МэВ. Ыдырау формуласы Өтімділік қабілеті жоғары.

3. г-бөлшектер ағыны. Г-жиілігі өте жоғары квант ағыны (10-10). Заряды жоқ. Спектрі сызықты. Энергиясы Е= 10КэВ 10МэВ. Заттан өту қабілеті өте жоғары.г-сәулелері зат арқылы өткенде оның әрі электрондарымен, әрі ядросымен де өзара әсерлесе алады.

Атом ядросының құрылымы. Ядро моделі. Атом ядросы оң зарядталған протоннан және заряды жоқ нейтронннан тұрады. Бұл бөлшектерді нуклондар дейді.

Протон. Протонның массасы m=938,26 МэВ немесе mp= 1836mэ. Спині s=1/2. магнит моменті μр = +2,79μя, мұндағы μя ядролық магнетон. Магнит моментінің өлшем бірлігі μя= eћ/(2mpc)

Нейтрон. mn =939,26 МэВ6 спині s=1/2. магнит моменті μn=-1,91 μя. “-” таңбасы механикалық моменті магнит моментіне қарама- қарсы екенін көрсетеді. Ядродағы протондар саны Менделеев кестесіндегі z элементінің атомдық нқміріне тең. Заряды +ze, массалық саны A=z+N тең, N- нейтрондар саны.

Ядро моделі.

ядролық тамшы моделі. Атом ядросындағы нуклондардың орналасуы су тамшысындағы молекулалардың тәртібіне ұқсас. Су тамшысындағы молекулалардың әсерлесуі қанша мерзімді және олардың қанығу қасиеті болады. Ядроның көлемі тамшы көлемі сияқты оларды құрайтын бөлшектер санына пропорцционал болады.

ядроның қабықша моделі. Паули принципіне сәйккес ядродағы нуклондар дискретті энергетикалық деңгейлерде (0абы0шаларда) орналасады. Толтырылған қабықшалары бар ядро орнықты болады.

Бір багыттагы ж/е озара перпендикуляр тербелістердіт косу. Векторлык диаграмма. Согу. Х осін карастырайык (1-сурет). Х осіне бурыш жасайтын узындыгы а векторын саламыз. Егер берілген векторды w бурыштык жылдамдыкпен айналдырсак, онда вектор ушынын проекциясы Х осі бойынша –а-дан +а-га дейінгі аралыкта козгалады ж/е бул проекциянын координатасы уакыт б/ша 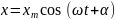занымен озгереді, бул гармоникалык тербеліс. Олай болса, гармоникалык тербелістін узындыгы тербеліс амплитудасына тен, ал вектордын багыты Х осімен тербелістін бастапкы фазасына тен бурыш жасайтын вектор аркылы беруге болатынын кореміз. Сурет-1 Сурет-2

Багыттары бірдей тербелісті косу . багыттары ж/е жиіліктері бірдей 2 гармоникалык тербелістерді косайык.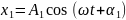 , 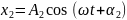Екі тербелісті 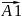ж/е 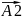векторлары аркылы орнектейік(2-сурет)Корыткы А векторынын ОХ осіне проекциясы гармоникалык тербелісті береді, екінші жагынан х=х1+х2.будан гармоникалык тербелістеді косу. Векторларды косу амалымен орнектеуге болады. суретте корыткы гармоникалык тербелістін амплитудасы 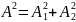+2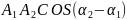 фазасы tg=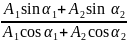

Егер фазалар айырмасы 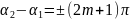(m теріс емес бутін сан) тен болса, корыткы амплитудасы А=А1+А2 шамасына тен, ал егер 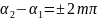, 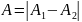бірінші жагдайда фазалары бірдей де, 2-де карама-карсы. Егер 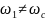болса, корыткы тербеліс гармоникалык емес болады, бірак 2 тербеліс жиіліктері аздап озгешелеу болган жагдайда корыткы тербеліс амплитудасы толыксымалы гармоникалык тербеліс ретінде карастыруга болады. бундай тербеліс согу д.а. 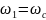ал 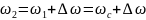, 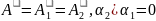деп белгілесек тербеліс тендеулері 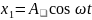, 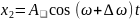. , корыткы тербеліс тендеуі 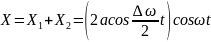шамасына тен. Мундагы 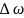согудын циклдык жиілігі. Периоды 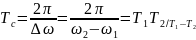,жиілігі 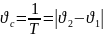амплитудасы A 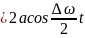Жиіліктері біодей озара перпендикуляр тербелістерді косу Х ж/е

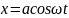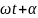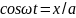У координата остерінін бойымен жиіліктері бірдей 2 тербелістерді косайык. Бастапкы фазасы 0-ге тен 1-ші тербелістін тендеуі , 2-сі y=вcos( ) 1-ші тендеуден ж/е sin 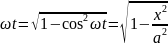онда 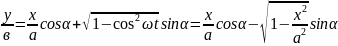турленуден кейін 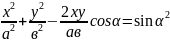бул элиппстін тендеуі. Кейбір жагдайлардагы тербеліс траекториясынын пішінін карастырайык.1-ші фазалар айырмасы 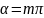, (m=… -1,0,1,2…), болса,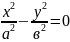 будан y= 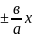тузудін тендеуі шыгады, + танбасы m мәні жуп болып, тербелістердін фазалары бірдей, ал – танбасы m мәнә так болып, фазалары карама-карсы болады. корыткы тербелістін амплитудасы A=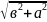 , фазасы 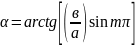тербелісті сызыкты поляризацияланган д.а.

сурет-9

2. 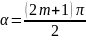, тербеліс тендеуі былай жазылады 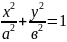эллипс остері ОХ ж/е ОУ остеріне сәйкес келеді. Егер а=b болса, эллипс шенберге айналады.Тербелісті донгелек бойынша поляризацияланган д.а. лиссажу фигуралары.Озара тербеліс-тердін жиіліктері әр турлі болса, онда корыткы тербелістен траекториясы Лиссажу фигураларын береді.

Сурет-10

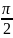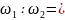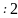Суретте фазалар айырмасы , ал жиіліктер катынастары 1 ж/е 3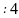 болатын тербелістердін траекториясы берілген.

Бір саңылаудығы дифракция. Монохромат жарық параллель шоғырының жолында өте тар а саңылауы бар АВ бөгеті тұрсын.

Сөйтіп түскен жарық толқынынның жазық бетінің саңылауы арқылы бір бөлігі ғана өте алады. Сондықтан толқындық беттің саңылаудың жазықтығына дәл келңп тұрған бөлігінің барлық нүктелерінің тербеліс фазалары бірдей болады. Гюйгенс принципі б/ша, толқындық беттің бұл бөлігінің әрбір нүктесі тербеліс көздері болып, олардың барлық жаққа жарық тербелістері таралады. Сонда бастапқы бір 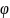бұрышын жасайтын бағыт бойывнша таралған сәулелер шексіз алыстағы нүктеде қиылысқанда н/е жинағыш (Л) линзаның бас фокус жазықтығында (С нүктесінде) тоғысқанда қандай қүұбылыс байқалады соны көрелік.Ол үшін толқындық бетті МN бағытына перпендикуляр, бірөбірінен қашықтығы 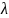/2-ге тең, бірнеше параллель жазықтықтар жүргізіп Френель зонасына бөлеміз. Сонда а саңылауынан өткен екі шеткі сәулелердің оптикалық жолдар айырмасы мынаған тең болады: 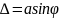Егер берілген бағытына қарап бөлгенде саңылау жұп зоналарға бөлінсе,онда сол бағытпен таралған жарық бірін-бірі өшіреді,өйткені әрбір тақ зонаның әсерін оған көршілес екі жұп зонаның әскрлері жойып жібереді. Сонда саңылаудың мөлшері а және толқын ұзындығы тұрақты ьолса,онда саңылауға сиятын зоналар саны n тек бұрышқа тәуелді болады.Олай болса, зоналар саны жұп болса,онда бақылау нүктесіндегі жарық нашар болып көрінедіде оның мин шарты: 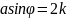/2 мұндағы,k=1,2,3…. Егер де зоналар саны тақ болса,онда С нүктесінде жарықтың күшейтетіндігін байқаймыз. 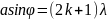Бұл кездегі интерференциялық бейненің максимум болу шарты: /2

Дифракциялық торлар-бірдей өзара параллель орналасқан саңылаулар жиынтығы.Мөлдір саңылаудың ені b,ал күңгірт(мөлдір емес)-а деп белгілесек дифракциялық тордың периоды d=b+a өрнегімен анықталады.

Кеңістік тордағы дифракциялық құбылыстар. Кристалдағы атомдарды көлемдік дифракциялық тор ретінде қарастыруға болады.Біз білетіндей дифракция құбылысын байқау үшін атомдардың арақашықтығы түскен толқын ұзындығымен шамалас болуға тиіс.Бұған рентген сәулелерінің толқын ұзындығы сәйкес келеді ̴10^-10м. Олай болсы рентген сәулелері кристалдық тордан өткенде дифракцияланады(сурет)

Егер кристал бетінде толқын ұзындығы монохроматты рентген сәулелері бұрыш жасап түссе,атомдық жазықтығында жатқан атомдардан шағылады. Шашыраған 1және 2 сәулелерініңоптикалық жолдарының айырмасы 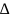=2dsinф. Интенсивтілігі max болу үшін мына шарт орындалу керек 2dsin =k к-шағылғын сәулелердің реттік саны. Осы теңдеуді Вульф-Бреггер формуласы деп атайды.

Голография-(грекше-«толық жазу»)-интерференциялық көріністерді толық жазып және оны қалпына келтіретін ерекше тәсіл.Голография интерференция құбылысына негізделгеннен кейін қабаттасқан толқындар когерентті болуы тиіс,сондықтан лазеолерді қолданады.Фото суреттерде тек заттан шағылған толқындардың амплитудасы тіркеледі,ал кеңістік голографиясында фазада тіркелуі қажет. Сонымен голография негізі мынада:нәрседен шығарылған толқындар мен оған когерентті фазасы белгілі жарық көзінен келген толқындардың интерферениясынарнаулы пластикаға түсіріліп,голограмма алады.

Бөлшектердің потенциалды тосқауыл арқылы өтуі. Туннельдік эффект. Кванттық және классикалық физикалардың айырмашылығын көрсететін туннельдік эффект болып табылады. Классикалық механикада егер бөлшектің энергиясы тосқауыл энергиясынан аз болса бөлшек тосқауылдан өте алмайды, ал кванттық физикада өту ықтималдығы бар. Бұл бөлшектің толқындық қасиетімен түсіндіріледі.U биіктігі, d ені болатын потенциалдық тосқауылдың сол жағынан келіп түсетін бөлшекті қарастырайық.

Бөлшектің энергиясы тосқауыл потенциалының энергиясынан кем E<U. Шұңқыр ішіндегі бөлшек үшін Шредингер теңдеуін жазайық:

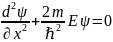
Ал сыртындағы күйі үшін :

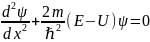
Осы екі дифференциалдық теңдеулердің шешімі:

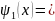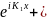1 аймақ үшін x<0, A₁ В₁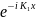

2 аймақ үшін 0≤x≤d, 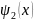= А₂ + В_{2 ,}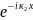

3аймақ үшін x>d, 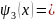A₃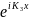

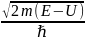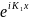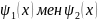Мұндағы K₁= , К₂= ; A₁ және В₁ тосқауылға түсетін, шағылатын де-Бройль толқындары А_{2 ,} х=0 шекарасынан сынып өткен толқын, ал В_{2 ,}х=а шекарасынан шағылған толқын A₃ тосқауылдан өтіп қайта оралмайтын толқын. Тосқауылдан өту коэффициентін табу үшін х=0 шекарасында , ал х=d шекарасында 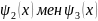функцияларымен оның туындыларын теңестіреміз. A₁ В₁ А₂ В₂ A₃ коэффициенттері бар төрт теңдіктер арқылы өту D және R шағылу коэффициенттерін табайық: x=0 болғанда ;

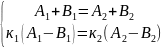x=d болғанда 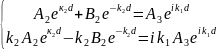; Теңдіктерді A₃ өту коэффициенті үшін шешіп 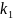, 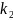мәндерін қойсақ D= 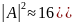теңдігін аламыз. 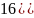тең олай болса D= 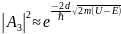. Берілген формуладан тосқауыл мен бөлшектің энергиясы мен тосқауылдың ені көп болып және бөлшектің массасы ауырлау болса өту ықтималдығы аз болады. Бөлшек энергиясының тосқауыл биіктігінің энергиясынан аздығына қарамастан тосқауылды өту құбылысы тунелдік эффект д.а. Тунелдік эффектісіне мынадай мысал жатады: жартылай өткізгіштің түйіспе жеріндегі электрондардың өтуі, металдың салқын күйіндегі электрондардың эмиссиялық құбылысы, ядролық физикада болатын α–ыдырау құбылысы. Егер потенциалдық тосқауылдың формалары әр түрлі болса, онда бөлшектердің өту ықтималдығы мына формуламен есептеледі: w= . 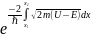Тунелдік эффект тек кванттық тұрғыда түсіндіріледі. Біріншіден кванттық теория бойынша кез келген бөлшек де Бройль толқыны ретінде қарастырылады, толқынның интенсивтілігі бөлшектердің өту ықтималдығын береді, олай болса Шредингер теңдеуінің шешімі бөлшектердің потенциалдық тосқауылдан өтетіндей нолге тең болмайтын ықтималдығын көрсетеді. Екіншіден Гейзенбергтің анықталмаушылық қатынасынан бөлшектің импульсі мен координатасын бір мезгілде мәндері болмайды. Олай болса бөлшек бір мезгілде кинетикалық (импульс) және потенциалдық (координатасы) энергиялардың мәндері болмайды. Сондықтан, бөлшектің толық энергиясы осындай ал потенциалдық энергиясы мынандай деп алуға болмайды.