
2.2. Розробка та побудова моделей.
За наявними даними побудовано графіки залежності показника від кожного фактора, а також побудовано лінію тренда, але тільки для парних моделей.
Лінія тренда – це уявна лінія, навколо якої групуються дослідні дані.
Подальший аналіз кожної моделі виконується за допомогою лінійної функції.
Спочатку розглядається вплив кожного фактора окремо (парні моделі у-х1; у-х2; у-х3), потім двох факторів разом (моделі у-х1, х2; у-х2, х3; у-х1, х3).
Також знаходимо ще одну характеристику тісноти зв’язку між показником і фактором, який називається індексом кореляції – R.
За своїм значенням індекс кореляції збігається з кореляційним відношенням. Тобто, чим ближче R до одиниці, тим тісніший зв’язок між ознаками.
Для оцінки надійності кореляційних характеристик використовується критерій Фішера, який визначається за формулою:
F = ∂² k2 / ϭ² k1
де k1 = К - 1; k2 = n – K – ступені вільності для міжгрупової і середньої з групових дисперсій;
n – кількість елементів досліджуваної сукупності;
К – число груп, на які поділена сукупність.
Фішер знайшов розподіл відношень дисперсій і розробив відповідні математичні таблиці, в яких наводиться F-критерій теоретичний F теоретичний при ймовірностях 0,95 і 0,99. Якщо розрахунковий критерій Фішера більший за табличний з даною ступінню довіри, значить між показником і фактором існує зв’язок з цією ступінню довіри. Якщо ж розрахунковий критерій менший табличного, то різниця між дисперсіями зумовлена впливом випадкових факторів.
2.2.1. Парні моделі.
Парна модель є базовою моделлю впливу кожного фактора.
Побудова виконується двома способами на кожну модель:
за побудовою лінії тренда;
за допомогою статистичної функції Лінійна (глибокий статистичний аналіз).
Загальне рівняння: y = ax + b;
∂y / ∂x = a.
а – коефіцієнт, що визначає швидкість зміни показника від фактора (тобто визначає силу впливу фактора на показник).
Парна модель №1 y - x1 |
|||
№ |
рік |
Cu, мг/кг |
Кількість овочевих культур, у яких спостерігалось пригнічення росту на 1 тис. рослин |
|
|
X1 |
Y |
1 |
1984 |
1,25 |
30 |
2 |
1985 |
1,5 |
33 |
3 |
1986 |
1,5 |
35 |
4 |
1987 |
1,5 |
38 |
5 |
1988 |
1,6 |
41 |
6 |
1989 |
1,9 |
41 |
7 |
1990 |
1,9 |
43 |
8 |
1991 |
2 |
45 |
9 |
1992 |
2 |
47 |
10 |
1993 |
2,1 |
49 |
11 |
1994 |
2,2 |
50 |
12 |
1995 |
2,3 |
54 |
13 |
1996 |
2,6 |
50 |
14 |
1997 |
2,7 |
55 |
15 |
1998 |
2,8 |
57 |
16 |
1999 |
2,8 |
65 |
17 |
2000 |
2,9 |
66 |
18 |
2001 |
3,1 |
68 |
19 |
2002 |
3,3 |
69 |
20 |
2003 |
3,7 |
73 |
21 |
2004 |
3,9 |
74 |
22 |
2005 |
4 |
78 |
23 |
2006 |
4,2 |
80 |
|
Функція Лінійна |
|
|
a |
b |
|
16,86582606 |
11,6086324 |
|
0,766339147 |
2,032652448 |
R2 |
0,958445918 |
3,141970188 |
Критерій Фішера |
484,3655102 |
21 |
|
4781,645012 |
207,3115099 |
Коефіцієнт корреляціі |
0,979002512 |
|
Критерій Фішера табличний |
248,309371 |
модель адекватна |
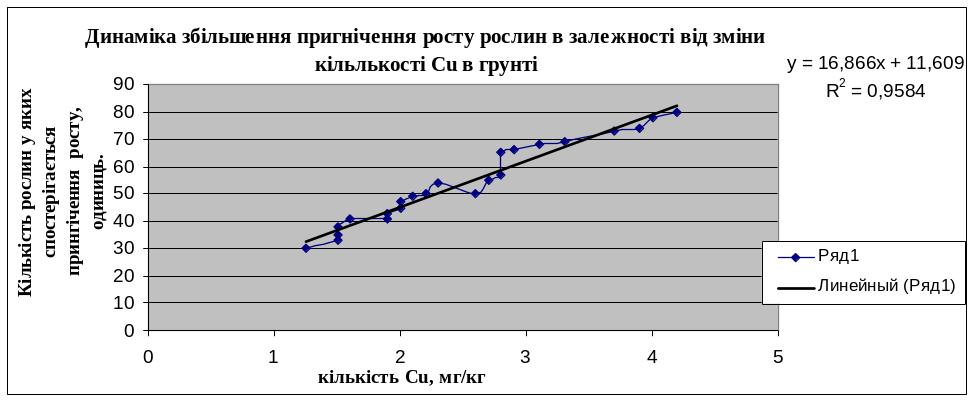
За проведеними розрахунками отримано рівняння y-x1; y=16,865x2+(11,608).
За розрахунком критерію Фішера встановлено ступінь адекватності моделі – модель адекватна, оскільки розрахунковий критерій більший за табличного.
Коефіцієнт кореляції становить 0,979, а отже, зв’язок між впливаючим фактором та показником є досить тісним.
Парна модель №1 y - x2 |
|||
№ |
рік |
Pb, мг/кг |
Кількість овочевих культур, у яких спостерігалось пригнічення росту на 1 тис. рослин |
|
|
X2 |
Y |
1 |
1984 |
4,9 |
30 |
2 |
1985 |
5 |
33 |
3 |
1986 |
5 |
35 |
4 |
1987 |
5,1 |
38 |
5 |
1988 |
5,2 |
41 |
6 |
1989 |
5,3 |
41 |
7 |
1990 |
5,4 |
43 |
8 |
1991 |
5,4 |
45 |
9 |
1992 |
5,5 |
47 |
10 |
1993 |
5,6 |
49 |
11 |
1994 |
5,7 |
50 |
12 |
1995 |
5,8 |
54 |
13 |
1996 |
5,9 |
50 |
14 |
1997 |
6,1 |
55 |
15 |
1998 |
6,2 |
57 |
16 |
1999 |
6,3 |
65 |
17 |
2000 |
6,5 |
66 |
18 |
2001 |
6,7 |
68 |
19 |
2002 |
6,9 |
69 |
20 |
2003 |
7,1 |
73 |
21 |
2004 |
7,3 |
74 |
22 |
2005 |
7,6 |
78 |
23 |
2006 |
8 |
80 |
|
Функція Лінійна |
|
|
a |
b |
|
16,51686228 |
-45,50371416 |
|
0,734084187 |
4,466754953 |
R2 |
0,960170549 |
3,076078197 |
Критерій Фішера |
506,2480426 |
21 |
|
4790,249123 |
198,7073986 |
Коефіцієнт корреляціі |
0,979882926 |
|
Критерій Фішера табличний |
248,309371 |
модель адекватна |
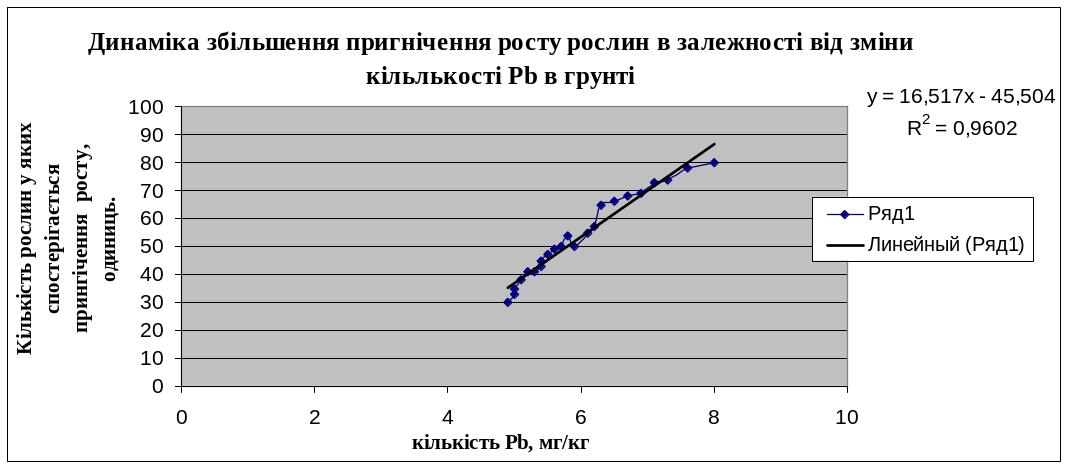
За проведеними розрахунками отримано рівняння y-x2; y=16,516x2+(-45,503).
За розрахунком критерію Фішера встановлено ступінь адекватності моделі – модель адекватна, оскільки розрахунковий критерій більший за табличного.
Коефіцієнт кореляції становить 0,979, а отже, зв’язок між впливаючим фактором та показником є досить тісним.
Парна модель №1 y - x3 |
|||
№ |
рік |
Zn, мг/кг |
Кількість овочевих культур, у яких спостерігалось пригнічення росту на 1 тис. рослин |
|
|
X3 |
Y |
1 |
1984 |
0,2 |
30 |
2 |
1985 |
0,3 |
33 |
3 |
1986 |
0,3 |
35 |
4 |
1987 |
0,3 |
38 |
5 |
1988 |
0,3 |
41 |
6 |
1989 |
0,4 |
41 |
7 |
1990 |
0,4 |
43 |
8 |
1991 |
0,4 |
45 |
9 |
1992 |
0,5 |
47 |
10 |
1993 |
0,5 |
49 |
11 |
1994 |
0,5 |
50 |
12 |
1995 |
0,6 |
54 |
13 |
1996 |
0,6 |
50 |
14 |
1997 |
0,7 |
55 |
15 |
1998 |
0,7 |
57 |
16 |
1999 |
0,8 |
65 |
17 |
2000 |
0,9 |
66 |
18 |
2001 |
0,9 |
68 |
19 |
2002 |
1 |
69 |
20 |
2003 |
1,1 |
73 |
21 |
2004 |
1,2 |
74 |
22 |
2005 |
1,3 |
78 |
23 |
2006 |
1,4 |
80 |
|
Функція Лінійна |
|
|
a |
b |
|
42,05674896 |
25,97964091 |
|
1,834817303 |
1,373584456 |
R2 |
0,96156625 |
3,021701737 |
Критерій Фішера |
525,3947664 |
21 |
|
4797,212213 |
191,7443091 |
Коефіцієнт корреляціі |
0,980594845 |
|
Критерій Фішера табличний |
248,309371 |
модель адекватна |
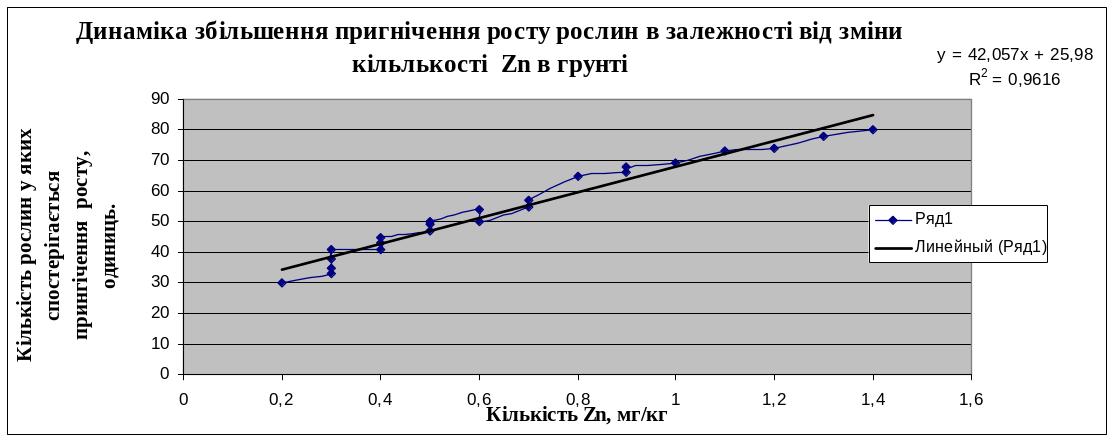
За проведеними розрахунками отримано рівняння y-x3; y=42,057x3+(25,908).
За розрахунком критерія Фішера встановлено ступінь адекватності моделі – модель адекватна, оскільки розрахунковий критерій більший за табличного.
Коефіцієнт кореляції становить 0,980, а отже, зв’язок між впливаючим фактором та показником є досить тісним.
№ п/п |
Рівняння |
ai |
R^2 |
Крит.Фішера |
1 |
y-x1; y=16,866x1+(11,609) |
16,866 |
0,9584 |
484,37 |
2 |
y-x2; y=16,517x2+(-45,504) |
16,517 |
0,9602 |
506,24 |
3 |
y-x3; y=42,057x3+(25,980) |
42,057 |
0,9616 |
525,39 |
Оскільки побудовані парні моделі мають високу точність ( за R^2 та критерієм Фішера), то можна зробити надійну оцінку окремих впливів діючих факторів. Найбільш впливовими (при окремій дії) є третій фактор – а саме вплив цинку, оскільки коефіцієнт а є найбільшими. А отже, перший і другиц фактори – вплив кобальту і міді – має незначний вплив на показник.
