Приложение 1 Методика решения оптимизационной задачи в пакете Еxcel

Для численного решения оптимизационной задачи используют инструмент Excel Поиск решения. Для запуска этого инструмента выполним команду Сервис/Настройки, в окне диалога «Надстройки» установим флажок на строке Поиск решения и нажнем кнопку ОК (рис. 1).

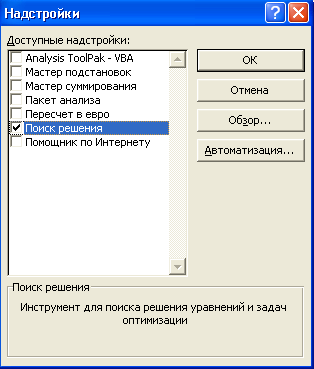
Рисунок 1 – Окно диалога «Надстройки»

После загрузки этого инструмента в списке опций ниспадающего меню Сервис появится новая команда Поиск решения. В результате выполнения этой команды появляется окно диалога (рис. 2).

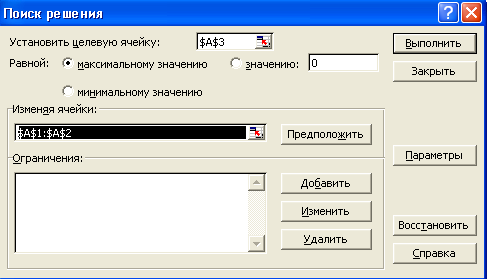
Рисунок 2 – Окно диалога «Поиск решения»

В поле ввода Установить целевую ячейку указывается ссылка на ячейку с целевой функцией, значения которой будут максимальным, минимальным или нулем в зависимости от выбранного переключателя.

В поле ввода Изменяя ячейки указываются ячейки, которые отведены под переменные целевой функции.

В поле ввода Ограничения добавления, изменения и удаления ограничений производятся с помощью кнопок Добавить, Изменить, Удалить.

Кнопка Параметры вызывает окно диалога «Параметры поиска решения», в котором возможно изменять параметры алгоритма поиска решения.

Для нахождения оптимального решения необходимо нажать кнопку Выполнить. После окончания расчета откроется окно диалога «Результаты поиска решения». Диалоговое окно Результаты поиска решения позволяет (рис. 3):

- сохранить на текущем рабочем листе найденное оптимальным решение;

- восстановить первоначальные значения;

- сохранить сценарий;

- выдать отчеты по результатам, устойчивости, пределам, необходимые для анализа найденного решения.

Если щелкнуть по кнопке ОК, то на месте исходной таблицы получим таблицу с найденными оптимальными значениями.

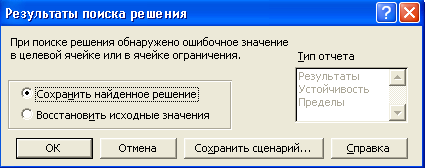
Рисунок 3 – Диалоговое окно «Результаты поиска решения»

Приложение 2

Методика построения корреляционной модели в пакете Еxcel:

1 Выбрать в Сервис / Анализ данных / Регрессия.

2 Заполнить поля в соответствии с запросами (рис. 4).

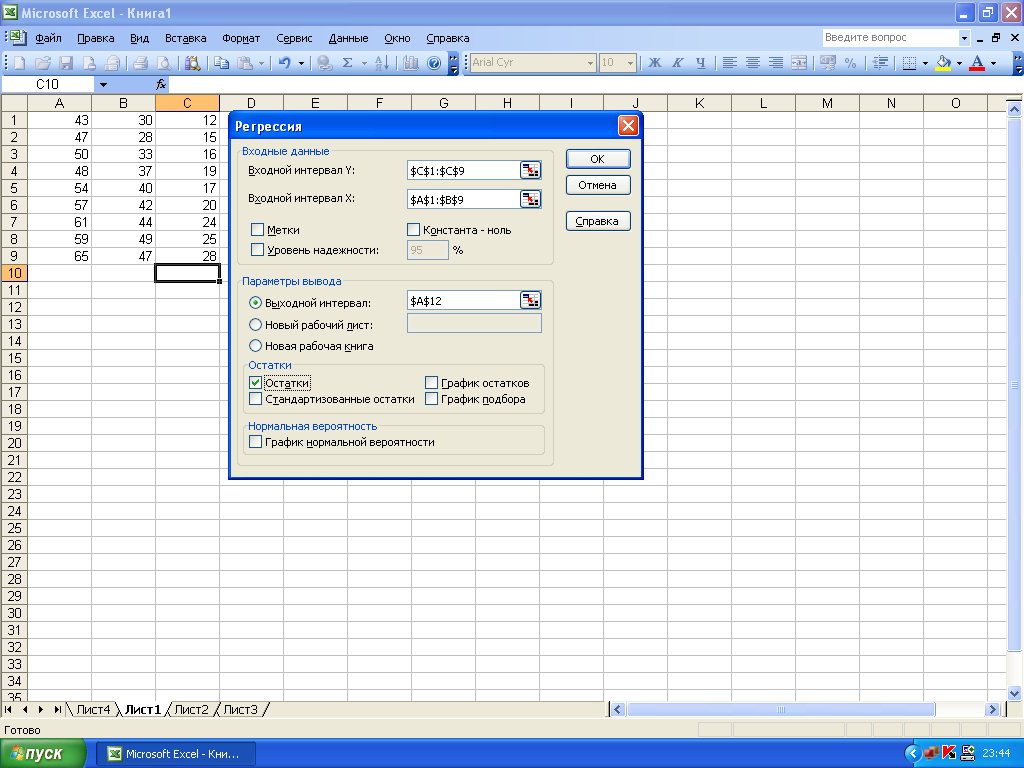
Рисунок 4 – Окно регрессии

3 Отчет по результатам (Вывод итогов) представлен на рисунке 5.

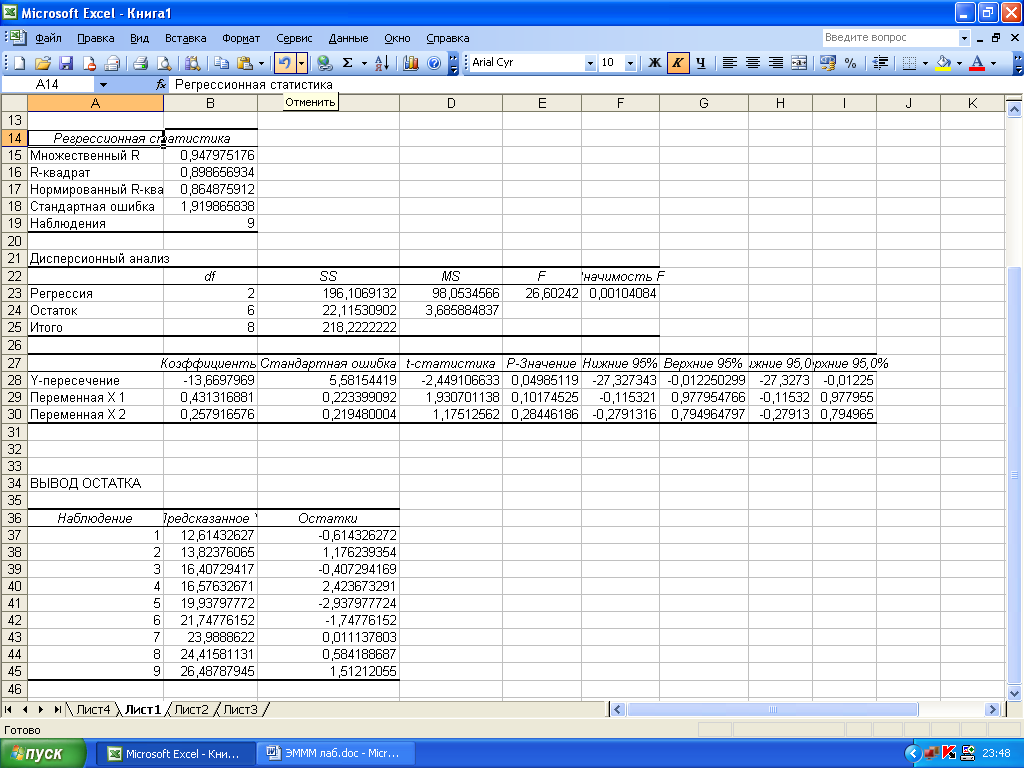
Рисунок 5 – Вывод итогов

Приложение 3

Оптимизация проекта по времени.

1. При построении сетевого графика (СГ) работы изображаются в виде стрелок, длины которых не зависят от продолжительности работы, и эти стрелки могут представляться под любым углом к оси абсцисс. События изображаются в виде кругов. На построенном графике события должны иметь упорядоченную нумерацию (i<j).

При построении СГ необходимо соблюдать следующие правила:

1 В СГ не должно быть работ, имеющих одинаковые номера.

2 Все события, кроме завершающего, должны иметь последующую работу. «Тупики» на СГ свидетельствуют либо об ошибке, либо указывают на то, что эта работа является лишней (событие 7 на рис. 6).

Рисунок 6

3 Не должно быть событий, в которые не входит ни одна из работ, поскольку условия их свершения не будут обеспечены (событие 3 на рис. 6).

4 В СГ не должно быть замкнутых контуров. Контур – это путь, начальная вершина которого совпадает с конечной (1-2-3-1на рис. 7).

Рисунок 7

5 Если событием начинается несколько работ, после завершения которых следует выполнение другой работы, то вводят фиктивные работы и дополнительные события (рис. 8)

а

а б г

б г

в в

Рисунок 8

1. если свершением какого-либо события начинается несколько работ, но для начала какой-либо работы (например а) не надо ждать свершения события 7 и можно ограничиться промежуточным результатом, то его представляют в виде самостоятельного события и работа а должна начаться с него (рис. 9).

а

б

б в

в а

Рисунок 9

2. если для начала работы д надо знать результат только работ б и в, а результат работы а не требуется, то необходимо ввести дополнительное событие 6 и фиктивную работу (рис. 10).

а г

а г

б д б д

в в

Рисунок 10

Пример: по данным таблицы 1 построить СГ.

Таблица 1

Работа	Предшествующие работы	Продолжительность, дней
А1	-	2
А2	-	4
А3	А1	3
А4	А1, А2	2
А5	А4	5
А6	А4	7
А7	А3, А5	3

СГ представлен на рисунке 11:

А₃

А₁ А₇

А₅

А₂ А₄ А₆

Рисунок 11

2. Сроки свершения и резервы событий определяют в 3 этапа:

• Прямой – вычисления начинаются с исходного события и продолжаются пока не будет достигнуто завершающее событие. Для каждого события вычисляется ранний срок его свершения по формуле: t_p(j)=max(t_p(i)+tij)

• Обратный – вычисления начинаются с последнего события и продолжаются пока не будет достигнуто начальное событие. Для каждого события рассчитывается поздний срок его свершения по формуле: tn(i)=min (tn(j)-tij)

• Вычисляются резервы времени событий по формуле: R (i)=tn(i)-tp(i)

Д анные этапы проводят на СГ. Для этого круг, изображающий событие делят на 4 сектора. В верхнем секторе записывают номер i события, в левом - ранний срок свершения события tp, в правом - поздний срок свершения события tn, в нижнем - резерв времени события Ri. В результате получают четырехсекторную диаграмму:

3. Критический путь находят следующим образом. Вначале определяют полные пути, начало которых совпадает с исходным событием, а конец – с завершающим. Затем рассчитывают продолжительности полных путей как сумму продолжительностей составляющих их работ. Полный путь, имеющий наибольшую продолжительность, является критическим. На СГ критический путь выделяется двойной или жирной линией. Критический путь проходит через события, не имеющие резервов времени.

4. Сроки выполнения работ и их резервы времени определяют по следующим формулам:

Ранний срок начала работы (i, j)

t_р.н(i, j) = t_p(i)

Ранний срок окончания работы (i, j)

t_p.o(i, j) = t_p(i) + t(ij)

Поздний срок окончания работы (i, j)

t_n.o(i, j) = t_n(j)

Поздний срок начала работы (i, j)

t_n.н(i, j) = t_n(j) - t(ij)

Полный резерв времени R_n(i, j) работы (i, j):

R_n(i, j) = t_n(j) - t_p(i) - t_ij = t_n(j) - t_p.o(i,j)

Cвободный резерв времени R_c(i, j) работы (i, j):

R_c(i, j) = t_p(j) - t_p(i) - t_ij = t_p(j) - t_p.o(i,j)

Результаты расчетов оформляют в сводную таблицу временных параметров работ следующего вида:

Таблица 32

№	Работа (i, j)	Продолжительность t(i, j)	Ранний срок		Поздний срок		Резерв времени
			начала работы	окончания работы	начала работы	окончания работы	полный	свободный