7. Оценка устойчивости сау

ПО АЛГЕБЮРАИЧЕСКИМ КРИТЕРИЯМ

В соответствии с теоремой А.М. Ляпунова устойчивость линейной системы автоматического управления устанавливается при решении характеристического уравнения, получаемого для передаточной функции САУ путем приравнивания к нулю знаменателя передаточных функций.

Для замкнутой системы характеристическое уравнение имеет вид:

Для разомкнутой системы характеристическое уравнение имеет вид:

В качестве алгебраического критерия для замкнутой САУ в курсовом проекте применяется критерий устойчивости Гурвица, по которому анализируется характеристическое уравнение для замкнутой системы

Если ввести в уравнение значения: А₀=0,000096, А₁=0,0068, А₂=0,15, А₃=1200, то характеристическое уравнение примет вид:

Так как получившееся характеристическое уравнение третьего порядка, то для того чтобы САУ была устойчива по алгебраическому критерию необходимо выполнения условий:

и .

Условие выполняется

Условие не выполняется

Так как выполняется только одно условие, то делаем вывод о неустойчивости САУ.

8.Оценка устойчивости сау по частотному критерию

Для частотного анализа САУ используется характеристическое уравнение построенное из передаточной функции в операторной форме с заменой р на (jω):

В результате замены получаем выражение для построения годографа Михайлова ( частотного критерия). Годограф – график построенный в комплексных координатах ( на комплексной плоскости).

При этом

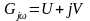, где U – вещественная величина, jV – мнимая величина

Подставляя в эти выражения различные значения ω построим годограф Михайлова (рис.3). Результаты расчетов сведены в таблицу№2.

Таблица №2

ω	0	5	10	20	50	70	100	150
U	1200	1199.8	1199.3	1197.2	1183	1167	1132	1047
V	0	0,738	1,404	2,323	-4,5	-22,4	-81	-301,5
ω	180	200	250	280	300	400	450	500
U	979,7	928	775	667	588	112	-177	-500
V	-532,8	-738	-1462,5	-2065,3	-2547	-6084	-860,5	-11925
ω	…	
U	…	-
V	…	-

Если замкнутая САУ обладает частотной устойчивостью, то график годографа начинается на положительной части вещественной оси в точке с координатой U_=0, проходит последовательно в положительном направлении (против часовой стрелки) N квадрантов комплексной плоскости и устремляется в бесконечность (N – порядок уравнения).

График годографа Михайлова, приведенный на рис.3 , начинается на положительной части вещественной оси, в точке U=1200, проходит в направлении «против часовой стрелки» первый и третий квадранты, но не охватывает начало координат и не проходит во втором квадранте комплексной плоскости.

Таким образом, оценка по частному критерию показала, что исходная САУ не обладает устойчивостью.

Рис. 3. Годограф Михайлова.