Вопросы

1. Что называется изгибом? Какие внутренние силовые факторы имеют место при изгибе и как они определяются?

2. Запишите дифференциальные зависимости между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом.

3. Приведите общие указания к построению эпюр поперечных сил и изгибающих моментов.

4. Как осуществляется расчет на прочность при изгибе?

5. Что представляет собой косой изгиб?

Практическое занятие № 8 Расчет основных геометрических характеристик зубчатых передач

Расчет основных геометрических характеристик зубчатых передач рассмотрим на примерах зубчатой цилиндрической и конической передач.

Расчёт цилиндрической зубчатой передачи

Главный параметр – межосевое расстояние, определяется по формуле:

,

где К_а – вспомогательный коэффициент; для косозубых передач К_а=43;

для прямозубых – К_а=49,5

– коэффициент ширины венца колеса; для косозубых передач ψ_а=0,25…0,40; для прямозубых – ψ_а=0,125…0,25

К_Нβ – коэффициент неравномерности нагрузки по длине зуба; для прирабатывающихся колёс К_Нβ=1

– допускаемое контактное напряжение.

Полученное значение межосевого расстояния округляется до стандартного из ряда: 40, 50, 63, 71, 80, 90, 100, 112, 125, 140, 160, 180, 200, 225, 250, 280, 315.

Модуль зацепления .

Полученное значение модуля округляем до стандартного из стандартного ряда чисел: 1; 1,25; 2; 2,5; 3; 4; 6; 8; 10.

Угол наклона зубьев β_min для косозубых колес .

Определяем суммарное число зубьев шестерни и колеса:

Полученное значение округляем в меньшую сторону до целого числа.

Уточняется действительная величина угла наклона зубьев для косозубых передач

Число зубьев шестерни .

Полученное значение округляется до ближайшего целого числа. Из условия уменьшения шума и отсутствия подрезания зубьев рекомендуется . Число зубьев колеса .

Фактическое передаточное число .

Фактическое межосевое расстояние .

Фактические основные геометрические параметры передачи:

Делительный диаметр:

шестерни , мм;

колеса , мм.

Диаметр вершин зубьев:

шестерни: , мм;

колеса , мм.

Диаметр впадин зубьев:

шестерни: , мм;

колеса , мм.

Ширина венца:

колеса мм;

шестерни , мм.

Дальнейшие расчеты ведутся по фактическим межосевому расстоянию и основным параметрам передачи.

Расчёт конической зубчатой передачи

Главный параметр – внешний делительный диаметр колеса:

,

где К_Нβ – коэффициент, учитывающий распределение нагрузки по ширине венца. Для прирабатывающихся колес с прямыми зубьями К_Нβ=1;

_Н – коэффициент вида конических колес. Для прямозубых колес _Н=1;

Полученное значение внешнего делительного диаметра колеса d_е2 округляем до ближайшего стандартного значения.

Углы делительных конусов шестерни δ₁ и колеса δ₂ :

δ₂ = arctg u; δ₁ = δ₂.

Внешнее конусное расстояние R_e = , мм. Значение R_e до целого числа не округляется.

Ширина зубчатого венца шестерни и колеса b = _R R_e,

где _R =0,285 – коэффициент ширины венца. Значение b округляется до целого числа по ряду R_а 40.

Приняв число зубьев шестерни , определяем число зубьев колеса . Фактическое передаточное число

Внешний окружной модуль .

Действительные углы делительных конусов шестерни δ₁ и колеса δ₂ :

δ₂ = arctg u_ф; δ₁ = δ₂.

Определяем фактические внешние диаметры шестерни и колеса.

Делительный:

шестерни , мм; колеса , мм.

Вершин зубьев:

шестерни , мм; колеса , мм.

Дальнейшие расчёты ведутся по фактическим внешним диаметрам передачи.

Пример чертежа передачи коническими зубчатыми колесами приведен на рисунке 1.

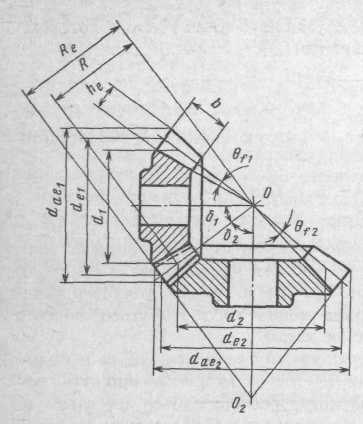
Рисунок 1.

Пример

Рассчитать основные геометрические параметры зубчатой цилиндрической косозубой передачи, если передаточное число зубчатой передачи , крутящий момент на тихоходном валу . Допускаемые контактные напряжения в зацеплении .

Решение

Определяем главный параметр – межосевое расстояние:

мм.

Полученное значение округляем до ближайшего из стандартного ряда, принимаем а_w=200 мм.

Модуль зацепления мм.

Полученное значение модуля округляем до стандартного из стандартного ряда чисел, принимаем мм.

Определяем суммарное число зубьев шестерни и колеса:

.

Полученное значение округляем в меньшую сторону до целого числа.

Число зубьев шестерни .

Число зубьев колеса .

Фактическое передаточное число .

Фактические основные геометрические параметры передачи:

Делительный диаметр:

шестерни мм;

колеса мм.

Диаметр вершин зубьев:

шестерни: мм;

колеса мм.

Диаметр впадин зубьев:

шестерни: мм;

колеса мм.

Ширина венца:

колеса мм;

шестерни мм.

Чертеж зацепления рекомендуется выполнить самостоятельно.

Задачи

1. Определить основные геометрические параметры зубчатой цилиндрической косозубой передачи, если материал шестерни – сталь 40, материал колеса – сталь 30, частота вращения быстроходного вала об/мин, передаточное число зубчатой передачи , требуемая мощность на тихоходном валу редуктора . Выполнить чертеж зацепления.

2. Определить основные геометрические параметры зубчатой конической передачи, если материал шестерни – сталь 45, материал колеса – сталь 35, частота вращения быстроходного вала об/мин, передаточное число зубчатой передачи , требуемая мощность на тихоходном валу редуктора . Выполнить чертеж зацепления.