Вопросы

1. Что называется кручением? Какой внутренний силовой фактор возникает при кручении и как его определить?

2. Какие напряжения возникают в поперечном сечении бруса при кручении и как они определяются?

3. Как определяется полный угол закручивания?

4. Как записывается условие прочности при кручении?

5. Как записывается условие жесткости при кручении?

Практическое занятие № 7 Изгиб

Прямой брус, работающий на изгиб, называют балкой. Рамой называют систему, состоящую из прямолинейных (реже криволинейных) стержней (брусьев), соединенных жестко между собой.

Поперечная сила Q_y представляет собой сумму проекций на ось Оу всех внутренних касательных сил, возникающих в поперечном сечении.

Изгибающий момент М_z представляет собой сумму моментов относительно оси Оz всех внутренних нормальных сил, возникающих в поперечном сечении.

Поперечная сила численно равна сумме проекций на ось Оу всех внешних сил, действующих на отсеченную часть рамы (балки).

Изгибающий момент численно равен сумме моментов всех внешних сил, действующих на отсеченную часть рамы (балки) относительно оси Оz.

Конечно, во всех случаях в число внешних сил входят и опорные реакции.

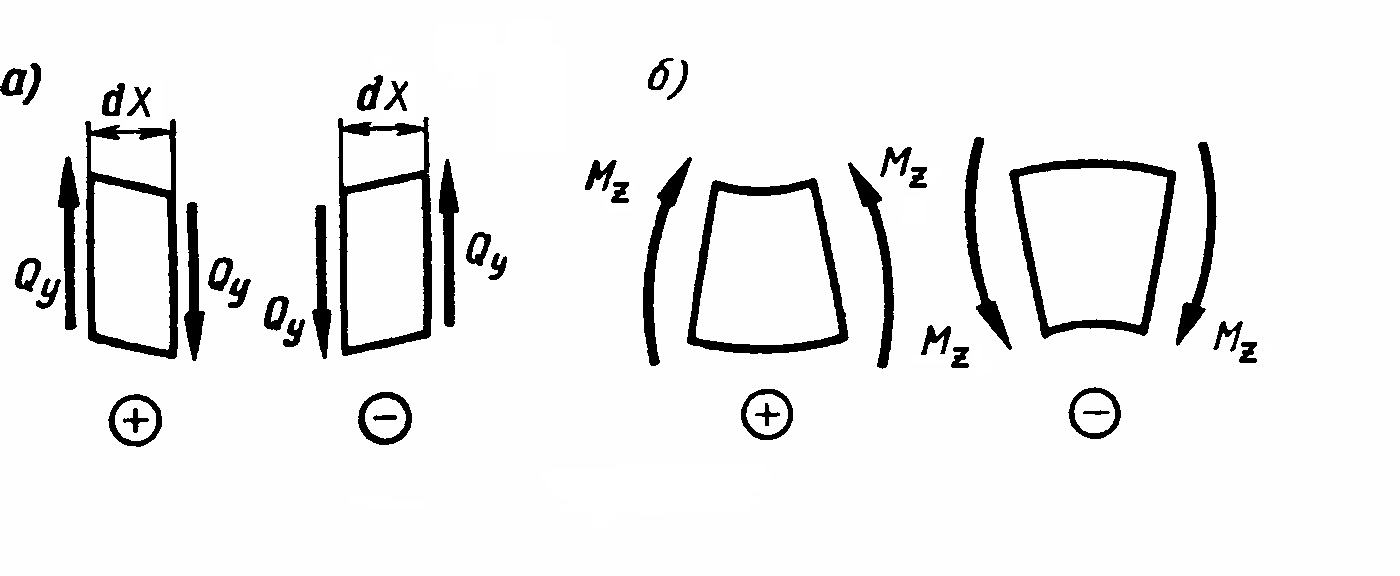
Рисунок 1 – Правило знаков для поперечных сил (а)

и изгибающих моментов (б)

Поперечные силы считаются положительными, если они стремятся повернуть элемент по часовой стрелке (рисунок 1, а). 3нак изгибающего момента связан с характером деформации бруса: изгибающий момент считается положительным, если элемент бруса изгибается выпуклостью вниз (рисунок 1, б), т. е. таким образом, что его сжатые волокна находятся в верхней части.

Построение эпюр поперечных сил и изгибающих моментов существенно упрощается при использовании дифференциальных зависимостей между интенсивностью распределенной нагрузки q, поперечной силой Q_y и изгибающим моментом М_z:

; ; .

Общие указания к построению эпюр поперечных сил и изгибающих моментов

1. Если на участке отсутствует распределенная нагрузка, то поперечная сила постоянна, а изгибающий момент изменяется по линейному закону.

2. Если на участке имеется равномерно распределенная нагрузка, то поперечная сила изменяется по линейному закону, а изгибающий момент – по закону квадратной параболы. При этом парабола всегда обращена выпуклостью навстречу распределенной нагрузке.

3. Если на участке имеется распределенная нагрузка, изменяющаяся по линейному закону (эпюра нагрузки – треугольник или трапеция), то поперечная сила изменяется по закону квадратной параболы, а изгибающий момент – по закону кубической параболы.

4. В сечении, где поперечная сила равна нулю, изгибающий момент достигает экстремального значения (максимального или минимального).

5. В сечении, где приложена внешняя сосредоточенная сила, перпендикулярная к оси элемента, эпюра Q имеет скачок на величину этой силы, а эпюра М – излом (смежные участки эпюры не имеют плавного сопряжения).

6. В сечении, где приложен внешний сосредоточенный момент, эпюра М имеет скачок на величину этого момента. На эпюре Q это не отражается.

7. В концевом сечении балки поперечная сила и изгибающий момент равны, соответственно, приложенным в этом сечении внешней сосредоточенной силе (активной или реактивной) и моменту сосредоточенной пары (активной или реактивной).

8. В сечении, где начинается или кончается распределенная нагрузка (при условии, что в этом сечении не приложена сосредоточенная сила), эпюра изгибающих моментов не имеет излома (парабола и прямая в этой точке имеют общую касательную).

Пример

Построить эпюры поперечных сил и изгибающих моментов для балки, изображенной на рисунке 1, а.

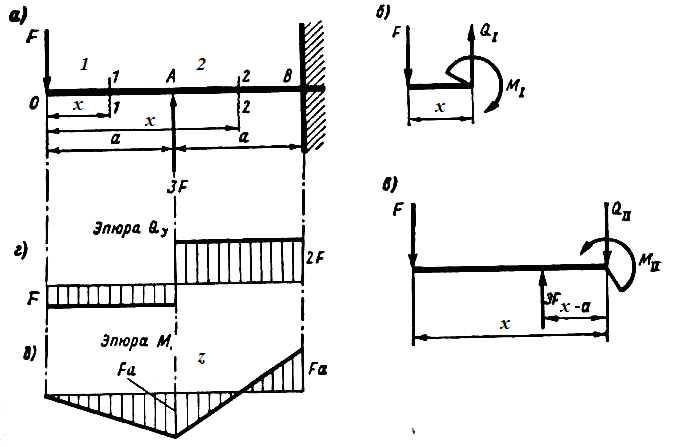
Рисунок 1

Решение

Заданная балка имеет два участка нагружения, границы которых совпадают с точками приложения внешних сил. Эти участки указаны на рисунке 1, а.

Построим эпюры поперечных сил и изгибающих моментов, пользуясь изложенными выше правилами.

Начнем с построения эпюры поперечных сил.

На участке 1 распределенная нагрузка отсутствует, следовательно . Величину и знак Q₁ определим, проводя произвольное сечение на этом участке (например, 1-1) и рассматривая равновесие левой отсеченной части, показанной на рисунке 1, б. Нагрузкой, действующей на левую отсеченную часть, является сила F, стремящаяся повернуть эту часть против хода часовой стрелки, следовательно, Q₁ отрицательна

На участке 1 эпюра Q – прямая, параллельная оси абсцисс.

Для участка 2 поперечная сила также постоянна. Проводя произвольное сечение на этом участке (например, 2-2) и рассматривая равновесие левой отсеченной части, показанной на рисунке 1, в, определим величину и знак Q₂. На левую отсеченную часть действуют силы F и 3F. Q₂ равна их алгебраической сумме

Q₂=–F+3F=2F.

Заметим, что в сечении, где приложена сила 3F, на эпюре Q получается скачок на величину 3F.

Эпюра поперечных сил, построенная по приведенным данным, показана на рисунке 1, г.

Переходим к построению эпюры изгибающих моментов М.

На участке 1 момент изменяется по линейному закону. На левом конце балки он равен нулю (здесь не приложено внешнего момента).

В произвольном сечении 1 участка (рисунок 1, б)

M₁=–Fz.

Знак минус поставлен потому, что сила F изгибает балку выпуклостью вверх, т. е. сжатые волокна находятся снизу. В сечении А

M_A=–Fa.

На участке 2 изгибающий момент также изменяется по линейному закону (рисунок 1, в)

M₂=–Fz+3F(z – a).

Момент от силы F отрицателен – эта сила изгибает балку выпуклостью вверх. Сила 3F изгибает балку выпуклостью вниз и, следовательно, соответствующий изгибающий момент положителен.

В сечении В изгибающий момент

M₃=–F2a + 3Fa = Fa.

Эпюра изгибающих моментов показана на рисунке 1, д.

Задачи

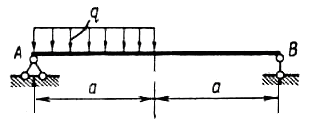
1. Для заданных балок (рисунок 2, а-в) построить эпюры поперечных сил и изгибающих моментов.

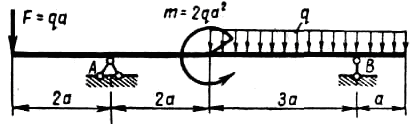
а)	б)
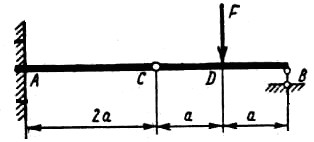
в) Рисунок 2