Практическое занятие № 4 Центральное растяжение-сжатие (теоретическая часть)

При растяжении или сжатии прямого бруса в его поперечных сечениях возникает только один внутренний силовой фактор – продольная сила N_х или N.

Продольные силы, соответствующие деформации растяжения, принято считать положительными, а сжатия – отрицательными.

Модуль и направление продольной силы определяются из уравнения равновесия, составленного для отсеченной части бруса:

или ,

(1)

откуда

,

(2)

т.е продольная сила, в произвольном поперечном сечении численно равна алгебраической сумме проекций на его продольную ось Oх всех внешних сил, приложенных к оставленной части.

В тех случаях, когда продольные силы в различных поперечных сечениях бруса неодинаковы, закон их изменения по длине бруса удобно представлять в виде графика, называемого эпюрой продольных сил. Аргументом при построении этого графика является координата поперечного сечения бруса х, а функцией – продольная сила N. Таким образом, эпюра продольных сил – это график функции .

При растяжении-сжатии бруса в его поперечных сечениях возникают только нормальные напряжения, которые определяются по формуле:

.

(3)

где А – площадь поперечного сечения бруса.

При растяжении напряжение считают положительным, при сжатии – отрицательным. В тех случаях, когда нормальные напряжения в различных сечениях бруса неодинаковы, целесообразно показывать закон их изменения по длине бруса в виде графика – эпюры нормальных напряжений.

В сечении, расположенном произвольно по отношению к оси бруса, при растяжении возникают также касательные напряжения. Наибольшее касательное напряжение возникает на площадке, наклоненной под углом 45 к оси бруса, и равно половине нормального напряжения, возникающего в соответствующей точке поперечного сечения

.

(4)

Отношение приращения длины элемента к его первоначальной длине называется относительным удлинением или продольной деформацией:

(5)

Отношение изменения размера поперечного сечения к его первоначальному значению, называется относительным поперечным сужением или поперечной деформацией:

.

(6)

При растяжении поперечные размеры бруса уменьшаются, тогда по правилу знаков величина отрицательная. Продольную и поперечную деформации называют также линейными деформациями.

Между продольной деформацией и соответствующим нормальным напряжением существует прямо пропорциональная (линейная) зависимость. Это положение называется законом Гука и записывается в виде

.

(7)

– модуль продольной упругости или модуль Юнга.

Модуль продольной упругости – физическая постоянная для каждого материала, характеризующая его жесткость. Для стали в расчетах принимают Па.

При простом растяжении или сжатии отношение поперечной деформации к продольной – величина постоянная для данного материала и называется коэффициентом поперечной деформации или коэффициентом Пуассона.

.

(8)

В общем случае изменение длины всего бруса

.

(9)

Когда поперечное сечение бруса или отдельного его участка постоянно и продольная сила во всех сечениях одинакова, изменение длины всего бруса или участка

.

(10)

При растяжении или сжатии бруса, его поперечные сечения перемещаются вдоль оси бруса. Эти перемещения являются следствием деформации.

В случае, представленном на рисунке 1, деформируется лишь левая часть бруса (участок АВ), а участок ВС перемещается как абсолютно твердое тело. Перемещения всех сечений этого участка одинаковы и равны удлиненной части АВ бруса:

(11)

Т.е., перемещение произвольного сечения бруса равно изменению длины участка, заключенного между этим сечением и заделкой.

Например, для сечения, отстоящего на расстоянии х от заделки (х a).

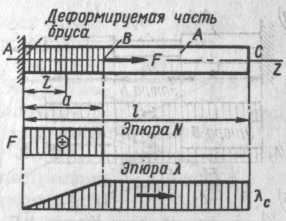
Рисунок 1 – Иллюстрация продольной деформации бруса

График , показывающий перемещение поперечных сечений в функции их расстояния х от неподвижного конца бруса, называемого эпюрой перемещений. Стрелкой на эпюре показано направление перемещений.

Работа внешних сил при статическом нагружении определяется теоремой Клапейрона: работа силы, статически приложенной к линейно-деформируемой системе, равна половине произведения конечного значения силы на конечное значение соответствующего перемещения, т.е.

.

(12)

Удельная энергия деформации определяется по формуле (в Дж/м³)

.

(13)

Пластичность материала оценивают значением относительного остаточного удлинения при разрыве

,

(14)

где – длины расчетной части образца после разрыва и до соответственно, и значением относительного остаточного сужения при разрыве

.

(15)

Прочность конструкции обеспечена, если возникающее в ней наибольшее напряжение не превышает допускаемого, т.е.

.

(16)

Условие прочности также можно записать в виде

,

(17)

где – предельный и расчетный коэффициенты запаса прочности соответственно;

– предельное и расчетное напряжения соответственно.

Системы, в которых количество неизвестных превышает количество независимых уравнений равновесия для данной системы, называются статически неопределимыми. Разность между количеством неизвестных и количеством независимых уравнений равновесия называется степенью статической неопределимости. Для решения такого рода задач надо помимо уравнений статики составить уравнения перемещений, основанные на рассмотрении деформации системы и применении закона Гука.