Вопросы

1. Что называется машиной? Какие машины различают в зависимости от их функционального назначения?

2. Дайте определение механизма. В чем сущность его анализа и синтеза?

3. Назовите основные составные части механизма.

4. Как определяется положение всех звеньев механизма относительно неподвижного звена (стойки)?

5. Какое количество простейших относительных движений может совершить свободное твердое тело? Что происходит при соединении звеньев в кинематические пары?

6. Как происходит разделение кинематических пар по классам? Приведите примеры кинематических пар различных классов.

7. Что представляют собой низшие и высшие кинематические пары? Приведите примеры.

8. Каким может быть замыкание элементов звеньев кинематических пар? Приведите примеры.

9. Что называется кинематической цепью? Приведите их классификацию.

10. Получите формулу подвижности кинематической цепи общего вида.

11. Каким образом получается структурная формула плоского механизма?

12. В чем заключается принцип образования механизмов по Асуру?

13. Приведите структурную классификацию плоских механизмов.

14. Что предполагает структурный анализ механизмов? Приведите пример.

15. Назовите основные задачи кинематического анализа механизмов.

Практическое занятие № 3 Структурный и кинематический анализ плоских механизмов (расчетная часть)

Пример 1

Определить степень подвижности и провести структурный анализ плоского механизма, представленного на рисунке 2.

Решение

Механизм имеет пять подвижных звеньев ( ) и семь кинематических пар 5-го класса ( ). По формуле (1) определяем степень подвижности механизма . Ведущее звено 1 со стойкой 6 образуют механизм 1-го класса. Ведомую кинематическую цепь можно разделить на две группы Ассура 2-го класса (выделены на рисунке 2 контурными линиями), начиная с группы, которая состоит из звеньев 4, 5. Так как механизм имеет в своем составе только группы Ассура 2-го класса, то его следует отнести к механизмам 2-го класса.

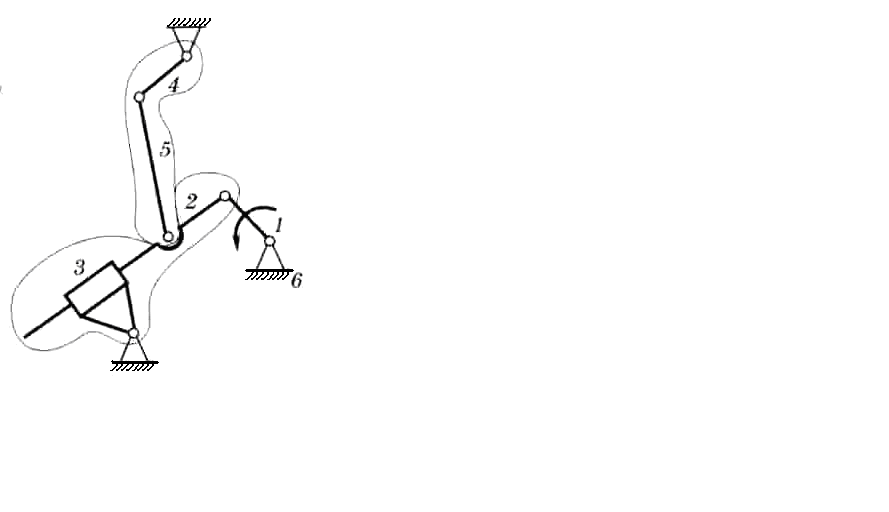
Рисунок 2 – Выделение структурных групп плоского механизма

Пример 2

Построить планы скоростей и ускорений для группы второго класса, изображенной на рисунке 3. Скорости и ускорения точек В и D считать известными.

Решение

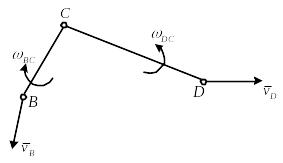
Рассмотрим построение планов скоростей и ускорений для групп второго класса (рисунок 3, а).

а) б)

Рисунок 3 – Построение плана скоростей

Пусть известны скорости и , тогда скорость точки С можно выразить двумя способами: разложив плоскопараллельное движение звена ВС на поступательное вместе с точкой В и на вращательное вокруг точки В, тогда

,

(2)

и разложив плоскопараллельное движение звена DС на поступательное вместе с точкой D и на вращательное вокруг точки D, тогда

(3)

Приравнивая (2) и (3), получим:

(4)

В этих формулах известны величины и направления векторов и , а также направления векторов и – , .

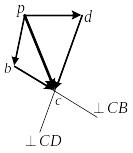
Для построения плана скоростей из произвольной точки р (рисунок 3, б) в масштабе откладываем вектора, изображающие скорости и . В конце векторов поставим точки b и d соответственно. Масштабный коэффициент . Находим скорость точки С, которая является общей для звеньев ВС и DС. Для этого из точек b и d проводим прямые, перпендикулярные ВС и DС соответственно. Пересечение данных перпендикуляров обозначим точкой с. Отрезок рс и будет определять скорость точки С в данный момент времени, тогда .

Угловые скорости звеньев определятся из равенств:

,	(5)
,	(6)

где , .

Для удобства графического построения плана скоростей всех звеньев группы иногда план скоростей условно поворачивают в одном и том же направлении (против хода часовой стрелки) на угол 90º. Такой план скоростей называется повернутым.

Для построения планов ускорений примем ,что векторы ускорений точек В и D известны, тогда

	(7)
	(8)

Решая (7) и (8) совместно, получим

(9)

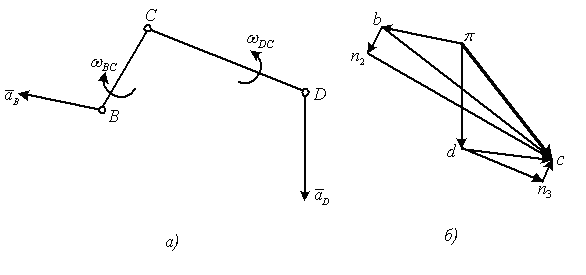
Рисунок 4 – Построение плана ускорений

Здесь – вектор нормального ускорения точки С в ее вращательном относительном движении вокруг точки В, направленный от точки С к точке В ( ); – вектор тангенциального ускорения в том же движении, направлен перпендикулярно ВC; – вектор нормального ускорения точки С в ее вращательном относительном движении вокруг точки D, направленный от точки С к точке D ( ); – вектор тангенциального ускорения в том же движении, направлен перпендикулярно DC.

Выбираем полюс плана ускорений (рисунок 4, б) и откладываем отрезки πb и πd, изображающие ускорения и в масштабе . Из точек b и d откладываем векторы и соответственно. Через конец вектора (точка ) проводим прямую, перпендикулярную ВС, а через конец вектора (точка ) – прямую, перпендикулярную DС, и в пересечении получаем точку с. Вектор изображает ускорение .

Задачи

1. Определить степень подвижности, количество кинематических пар, их тип, и провести структурный анализ плоских механизмов, представленных на рисунке 5 а, б.

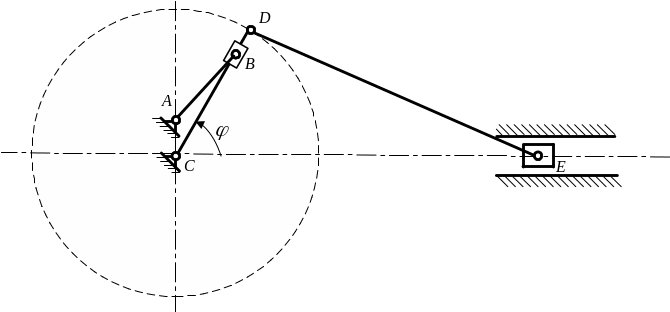
а)

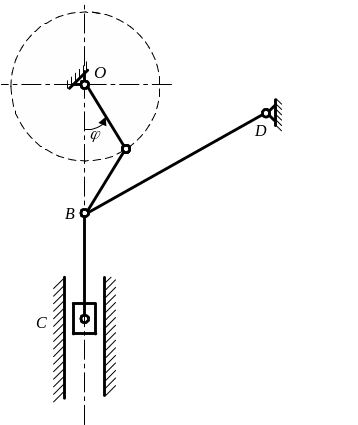
б)

Рисунок 5

2. Построить планы скоростей и ускорений для шарнирного четырехзвенника, изображенного на рисунке 6, если м, м, м, , рад/с.

Рисунок 6

3. Построить планы скоростей и ускорений для кривошипно-ползунного механизма, изображенного на рисунке 7, если м, м, , рад/с.

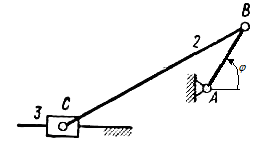
Рисунок 7