6.2. Признак Коши.

Теорема 2. Пусть дан знакоположительный ряд , для которого существует предел

1. Если q<1, то ряд сходится

2. Если q>1, то ряд расходится

3. Если q=1, то ряд может сходиться, а может и расходиться, т.е. надо проводить дополнительные исследования.

В дальнейшем понадобится следующее равенство

Пример 4. Исследовать на сходимость ряд

Решение: По признаку Коши данный ряд сходится.

6.3.Интегральный признак Коши.

Теорема 3. Пусть дан знакоположительный ряд , для которого существует функция, удовлетворяющая условиям:

1. f(x) определена, неотрицательна и непрерывна на промежутке [1, )

2. f(x)

3. f(n)=

Тогда данный ряд сходится или расходится одновременно со сходимостью или расходимостью несобственного интеграла

Доказательство. 1)Пусть интеграл сходится.

+ + + +M .

Последовательность частичных сумм ряда ограничена сверху, поэтому ряд сходится.

2) Пусть интеграл расходится.

Частичная сумма + + , равна площади ступенчатой фигуры от 1 до n+1 следовательно, < ак как интеграл расходится, то = . Поэтому последовательность частичных сумм ряда , неограничена сверху . Следовательно ряд расходится.

Пример 5. Исследовать на сходимость ряд Дирихле

Решение. Если s≤0, то общий член ряда к нулю не стремится, поэтому ряд расходится.

Пусть S>0. Для исследования данного ряда применим интегральный признак Коши.

Рассмотрим функцию f(x)= , которая удовлетворяет всем условиям теоремы 3 на промежутке [1,+ ). Рассмотрим интеграл при s

= =

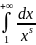Пусть s= 1

- интеграл расходится.

По интегральному признаку Коши, ряд Дирихле s>1 сходится, а при s расходится.

Лекция 7

Тема: Знакочередующиеся ряды. Теорема Лейбница. Ряды с произвольными членами. Абсолютная и условная сходимость ряда. Теорема о связи между абсолютной сходимостью и сходимостью ряда.

7.1 Знакочередующиеся ряды. Теорема Лейбница.

Определение 1. Ряды вида , либо называются знакочередующимися рядами.

Примерами знакочередующихся рядов являются:

- знакочередующийся гармонический ряд,

- знакочередующийся ряд Дирихле.

Теорема 1. (Теорема Лейбница)

Пусть в знакочередующемся ряде члены ряда по модулю не возрастают, т.е:

Для того, чтобы знакочередующийся ряд сходился необходимо и достаточно, чтобы предел общего члена равнялся нулю, т.е.

Доказательство. Рассмотрим для определенности ряд . Необходимость. Дано: Ряд сходится. Требуется доказать, что предел общего члена равен нулю.

Справедливость этого утверждения вытекает из необходимого признака сходимости ряда.

Достаточность. Дано: . Требуется доказать, что ряд сходится.

Сначала докажем сходимость последовательности частичных сумм с четными номерами

Имеем:

S₂ ≤S₄ ≤S₆ ≤…. ≤S_2n ≤…. ,

т.е. последовательность {S_2n}^∞ не убывает.

S_2n запишем в следующем виде:

Последовательность {S_2n} не убывающая и ограничена сверху, следовательно, она имеет предел:

Теперь рассмотрим последовательность частичных сумм ряда с нечётными номерами {S_2n+1} и найдём предел этой последовательности.

, т.к. по условию. Отсюда следует, что . Теорема Лейбница справедлива для рядов т.к. данный ряд получается из ряда умножением на (-1), что не меняет сходимости ряда. Для ряда справедливо равенство: |S|<|a₁|.