3.2 Определение криволинейного интеграла.

Пусть в пространстве задана спрямляемая кривая ВС, в каждой точке которой определён вектор (x,y,z).

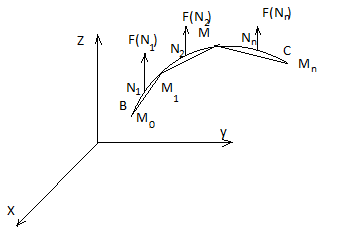
Кривую ВС произвольным способом разобьём на n частей точками В = = , , … = С, (Т).

Через обозначим наибольшее из длин участков разбиения.

В каждом из участков разбиения произвольным способом выберем по точке , … и составим сумму , которая называется интегральной суммой.

Предел интегральных сумм при называется криволинейным интегралом.

=

Запись криволинейного интеграла в координатной форме.

(x,y,z) = P(x,y,z) +Q(x,y,z) +R(x,y,z) , =dx +dy +dz

Напомним, что скалярное произведение двух векторов равно сумме произведений соответствующих координат. Следовательно,

= + + dz

3.3 Свойства криволинейного интеграла.

=- .

= + .

3.4 Вычисление криволинейного интеграла.

Пусть кривая задана параметрически

: , у которой (t),y’(t),z’(t) непрерывны

Будем предполагать, что P(x,y,z),Q(x,y,z) ,R(x,y,z) непрерывны на . В этом случае криволинейный интеграл сводится к вычислению определенного интеграла по формуле:

+ + dz= ]dt.

3.5 Механический смысл криволинейного интеграла.

Криволинейный интеграл равен работе по перемещению материальной точки из точки B в точку С под действием силы (x,y,z).

3.6 Примеры вычисления криволинейных интегралов.

Пример 1. Вычислить работу по перемещению материальной точки из начала координат по первому витку винтовой линии , 0 под действием силы =x +y +z

Решение.

А= = = = = = = 2 .

Пример 2. Вычислить криволинейный интеграл.

1. По параболе y= от точки В(0,0) до точки С(1,1), б) По отрезку прямой, соединяющего точки В(0,0) и С(1,1).

Решение:

Уравнение части параболы, соединяющей точки В и С, можно записать в параметрическом виде, считая х параметром.

ВС: , 0

= =0

Уравнение отрезка прямой можно записать в параметрическом виде, считая х параметром:

ВС: , 0

= dx = dx = =

Рассмотренный пример показывает, что криволинейный интеграл, вообще говоря, зависит от кривой, которая соединяет точки ВС.

Лекция 4

Тема: Формула Грина. Условия независимости криволинейного интеграла от пути интегрирования.

4.1 Формула Грина.

Формула Грина устанавливает связь между криволинейным интегралом по замкнутому контуру Г на плоскости и двойным интегралом по области, ограниченной данным контуром.

Замкнутый контур Г мы будем считать кусочно-гладким и без самопересечений.

Криволинейный интеграл по замкнутому контуру Г обозначается символом Замкнутый контур Г начинается в некоторой точке В этого контура и заканчивается в точке В. Интеграл по замкнутому контуру не зависит от выбора точки В.

Определение 1. Обход контура Г считается положительным, если при обходе контура Г область D остаётся слева. Г⁺ - контур Г обходится в положительном направлении, Г ^- - контур обходится в отрицательном направлении.

Теорема. Если P(x,y) и Q(x,y) непрерывны вместе со своими частными производными в ограниченной замкнутой области D, то справедлива формула Грина:

Где Г=

Г⁺ означает, что контур Г обходится в положительном направлении.

Доказательство. Доказательство проведем для односвязной области D, т.е. Г= состоит из одного замкнутого контура. При этом вначале будем предполагать, что любая прямая параллельная оси 0Х или 0Y пересекает Г не более, чем в двух точках.

Р ассмотрим двойной интеграл

.

(1)

Аналогично доказывается, что:

(2)

Из равенств (1) и (2) получаем:

Следовательно,

Формула Грина при сделанных предположениях доказана.

Замечание 1. Формула Грина остаётся справедливой, если граница Г области D некоторыми прямыми, параллельными оси 0Х или 0Y пересекается более чем в двух точках. Кроме этого формула Грина справедлива и для n-связных областей.