Лекция 12
Тема: Интегрирование функций комплексного переменного. Теорема Коши. Интеграл Коши. Особые точки. Вычеты.
12.1. Интегрирование функций комплексного переменного.
Пусть
дана произвольная функция w=
комплексного
переменного, определенная в некоторой
области G
комплексной плоскости переменного z,
и Г-произвольная спрямляемая линия,
лежащая в области G,
с началом в точке B
и концом в точке C.
Кривую BC
разобьем произвольным способом на n
частей точками B=z0,z1,z2,…,
zn=C
.Это разбиение обозначим через (Т). Пусть
,
где
.
В каждом из участков разбиения произвольным
способом выберем по точке ζ1,
ζ2,…,
ζn
и
составим сумму
,
которая называется интегральной суммой.
Предел таких интегральных сумм при
называется криволинейным интегралом
от функции
по кривой Г.
(1)
Имеем:
тогда интеграл
запишется в виде:
(2)
Формула (2) дает выражение интеграла по комплексному переменному через два криволинейных интеграла. Формулу (2) можно записать в следующем виде:
(3)
12.2. Вычисление интеграла от функции комплексного переменного.
Пусть
кривая Г задана в виде
,
тогда будем иметь:
,
где
Пример
1.
Пусть Г- кусочно-гладкая кривая,
соединяющая точки
.
Тогда
интеграл
Если
Г замкнутая кривая, то
.
12.3. Основные свойства интеграла функции комплексного переменного
1.
,
где Г+
и
Г‑
один и тот же путь, который проходится
в положительном и отрицательном
(противоположном) направлении.
2.
3
.
4.
5.
12.4. Теорема Коши. Вообще говоря, по двум различным путям, соединяющим две точки В и С, может иметь различные значения, т.е. интеграл может зависеть от пути интегрирования. Как и в случае с криволинейным интегралом возникает вопрос: какие условия надо наложить на функцию , чтобы не зависел от пути интегрирования.
Задача о независимости интеграла от пути интегрирования равносильна задаче нахождения условий, при которых данный интеграл, взятый по любому замкнутому контуру, равен нулю.
Итак,
предположим, что функция
является аналитической в односвязной
области G,
причем
непрерывны вместе с частными производными
первого порядка.
Так
как
является функцией аналитической в
области G,
то в этой области выполняются условия
Коши-Римана:
На основании формулы (2) имеем:
(4)
Рассмотрим
криволинейный интеграл
,
для которого
.
Так как
,
,
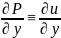то
в силу выполнения условий Коши-Римана
и поэтому
.
Аналогично
Учитывая
(4), имеем:
Итак, доказана следующая теорема.
Теорема Коши. Если является аналитической функцией в односвязной области G и непрерывны вместе с частными производными первого порядка, то интеграл от этой функции, взятый вдоль любого замкнутого контура, принадлежащего области G, равен нулю, т.е. Теорема Коши является основной теоремой в теории аналитических функций. Теорема Коши остается справедливой, если потребовать только, что является аналитической функцией в односвязной области G.